Numerical on Organ Pipes Class-11 Nootan ISC Physics Ch-28 Superposition of Waves-2 : Stationary (Standing) Waves : Vibration of Air Columns. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-11 Physics.
Numerical on Organ Pipes Class-11 Nootan ISC Physics Ch-28 Superposition of Waves-2 : Stationary (Standing) Waves : Vibration of Air Columns
| Board | ISC |
| Class | 11 |
| Subject | Physics |
| Book | Nootan |
| Chapter-28 | Superposition of Waves-2 : Stationary (Standing) Waves : Vibration of Air Columns |
| Topics | Numericals on Organ Pipes |
| Academic Session | 2025-2026 |
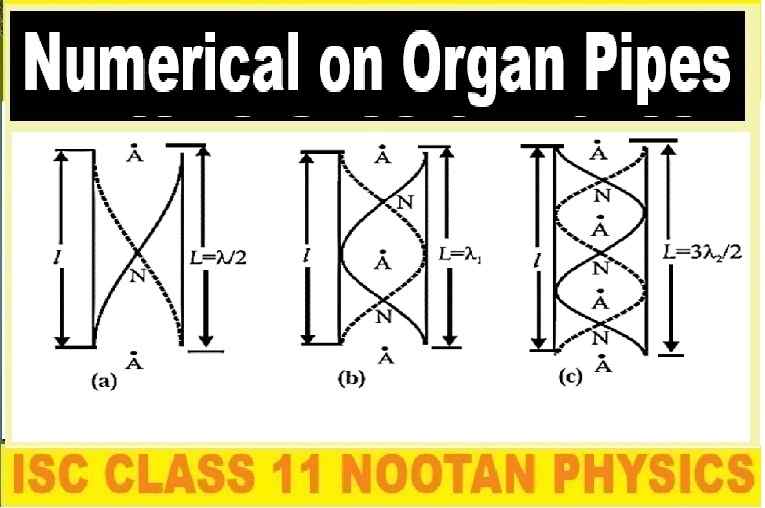
Numericals on Organ Pipes
Ch-28 Superposition of Waves- 2 : Stationary (Standing) Waves : Vibration of Air Columns
Q-6: What should be the minimum length of an open organ pipe for producing a note of 110 Hz? The speed of sound is 330 m s^-1.
Ans-6
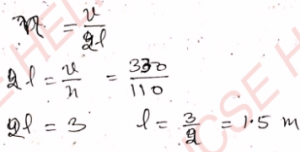
Q-7: The fundamental tone produced by an organ pipe has a frequency of 110 Hz. Some other frequencies in the notes produced by this pipe are 220, 440, 550, 660 Hz. Is this pipe open at both ends or open at one end and closed at the other? Calculate the effective length of the pipe. (Speed of sound = 330 m s^-1)
Ans-

Q-8: The difference in frequencies between the second overtone of a closed organ pipe and the first overtone of an open organ pipe of same length is 150. What are the fundamental frequencies of the closed and open pipes?
Ans-

Q-9: The sum of the frequencies of the first overtone of a closed pipe and the second overtone of an open pipe of the same length is 180 Hz. What are the fundamental frequencies of the closed and open pipes?
Ans-

Q-10: The fundamental frequency of an open organ pipe is 300 Hz. The frequency of the first overtone of another closed organ pipe is the same as the frequency of the first overtone of open pipe. What are the lengths of the pipes? The speed of sound is 330 m s^-1.
Ans-

Q-11: Two open organ pipes of lengths 75 cm and 80 cm are sounded together. How many beats per second will be produced by them? (Speed of sound in air = 332 m s^-1)
Ans-
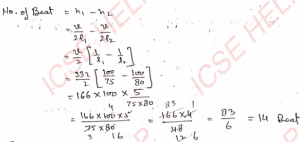
Q-12: Two organ pipes closed at one end are of equal diameters but different lengths. They produce 8 beats per second when sounded simultaneously. The smaller organ pipe is 16 cm long and the speed of sound in air is 320 m s^-1. Find the length of the other pipe.
Ans-

Q-13: Two open organ pipes on sounding simultaneously produce 5 beats/s. If the smaller pipe be 66 cm long, then determine the length of the bigger organ pipe. (The speed of sound in air is 330 m s^-1.)
Ans-

Q-14: Two open organ pipes of lengths 50.0 cm and 50.6 cm produce 4 beats/s. Calculate the speed of sound in air.
Ans-

Q-15: A tuning fork of frequency 256 Hz resonates with a closed organ pipe of length 25.4 cm. If the length of the pipe be increased by 2 mm, then calculate the number of beats produced per second.
Ans-

Q-16: Two tuning forks A and B when sounded together produce 8 beats per second. A and B are in resonance with closed organ pipes having lengths 32 and 33 cm respectively. Determine the frequencies of the tuning forks.
Ans- frequency of the tuning forks are 264 Hz and 256 Hz
Q-17: A tuning fork of frequency 341 Hz is vibrated just over a tube of length 1 m. Water is being poured gradually in the tube. What height of water column will be required for resonance? The speed of sound in air is 341 m s^-1.
Ans-

Q-18: A 1 metre long tube of glass is in vertical position and is completely filled with water. Water leaks slowly from the bottom. If a vibrating tuning fork of frequency 495 be brought at the upper end of the tube, then at what positions of the water-level will the resonance occur at 0°C? The speed of sound at 0°C is 330 m s^-1.
Ans-

Q-19: A 30 cm long pipe whose one end is closed and the other is open resonates at a minimum frequency of 274 Hz. Can this pipe resonate at other frequencies also? If yes, then give the values of two of them. Calculate also the speed of sound in air.
Ans-

Q-20: A resonance tube is resonated with a tuning fork of frequency 512 Hz. The lengths of two successive resonated air columns are 16 cm and 50 cm respectively. Find the speed of sound.
Ans-
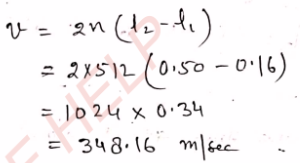
Q-21: A tuning fork of frequency 440 Hz is held at the open end of a closed pipe. If the distance between the closed and the open ends can be changed, then calculate the distance between the closed and the open ends for the first two resonances. Speed of sound in air is 330 m s^-1
Ans-
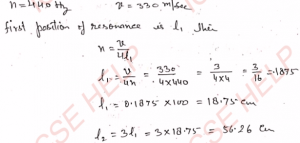
Q-22: A tuning fork of frequency 660 Hz is vibrated just above a pipe of length 75 cm filled with water. Water is gradually taken out of the tube. Find two positions of resonance from the upper end of the tube. Speed of sound in air is 330 m s^-1.
Ans-
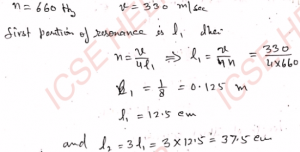
Q-23: When a sound source of frequency 300 Hz is held near the open end of a closed pipe, a loud sound is emitted from the pipe. Calculate the minimum length of the pipe and two other frequencies which may sound the pipe. Speed of sound = 330 m s^-1.
Ans-
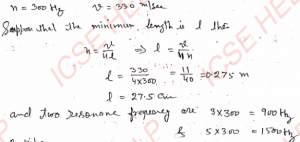
Q-24: A pipe closed at one end is in resonance of a vibrating tuning fork when the length of the air column is 25 cm. The next resonance occurs when the length of the air column is 77 cm. If the speed of sound in air be 338 m s^-1, then calculate the wavelength of the emitted note and the frequency of the fork.
Ans-
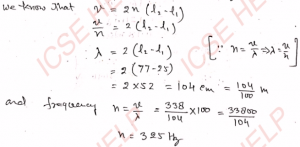
Q-25: In a resonance tube, the first and the second resonances are obtained at 22.5 cm and 70.0 cm respectively. Find out the end-correction and the length of the air column for the third resonance.
Ans-

Q-26: A 25 cm long closed organ pipe resonates with a tuning fork at 40°C. Determine the frequency of the fork. The speed of sound in air at 0°C is 330 m s^-1.
Ans-

Q-27: The length of a pipe open at both ends is 48.8 cm and its fundamental frequency is 320 Hz. Find the radius of the pipe. If one end of the pipe be closed, what will be the fundamental frequency? (Speed of sound = 320 m s^-1.)
Ans-

Q-28: The smallest length of a resonance tube closed at one end is 32.0 cm when it is sounded with a tuning fork of frequency 256 and 20.8 cm when sounded with a fork of frequency 384. Calculate the speed of sound and the end-correction.
Ans-

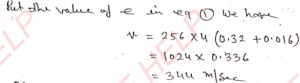
Q-29: A 0.75 metre long closed organ pipe is vibrating in its fundamental mode. If the temperature of the room be 15°C and the speed of sound in air at this temperature be 340 m s^-1, then determine the frequency of the note of the pipe. If the temperature rises to 25°C, then what will be the frequency? Consider the effect of temperature on the length of the pipe negligible.
Ans-

— : End of Numerical on Organ Pipes Class-11 Nootan ISC Physics Ch-28 Superposition of Waves-2 : Stationary (Standing) Waves : Vibration of Air Columns :–
Return to : – – Nootan Solutions for ISC Physics Class-11
Thanks
Please share with your friends


