OP Malhotra Area of Plane Figures Class-9 S.Chand ICSE Maths Ch-16

OP Malhotra Area of Plane Figures Class-9 S.Chand ICSE Maths Ch-16. We Provide Step by Step Answer of Exe-16(a), Exe-16(b), Exe-16(c), Exe-16(d), with Chapter Test of S Chand OP Malhotra Maths . Visit official Website CISCE  for detail information about ICSE Board Class-9.

OP Malhotra Area of Plane Figures Class-9 S.Chand ICSE Maths Ch-16

---

-: Select Topics :-

Exercise-16(a)

Exercise-16(b)

Exercise-16(c)

Exercise-16(d)

Chapter Test

---

Exercise-16

OP Malhotra Area of Plane Figures Class-9 S.Chand ICSE Maths Ch-16

Perimeter:

The length of the boundary of a closed figure is called the perimeter of the plane figure. The units of perimeter are same as that of length, i.e., m, cm, mm, etc

Area:

A part of the plane enclosed by a simple closed figure is called a plane region and the measurement of plane region enclosed is called its area.

Area is measured in square units.

The units of area and the relation between them is given below: 

Perimeter and Area of the Square:

● Perimeter of square = 4 × S.

● Area of square = S × S.

● Diagonal of square = S√2; (S is the side of square)

Perimeter and Area of the Triangle:

• Perimeter of triangle = (a + b + c); (a, b, c are 3 sides of a triangle)
• Area of triangle = √(s(s – a) (s – b) (s – c)); (s is the semi-perimeter of triangle)
• S = 1/2 (a + b + c)
• Area of triangle = 1/2 × b × h; (b base , h height)
• Area of an equilateral triangle = (a²√3)/4; (a is the side of triangle)

Perimeter and Area of the Parallelogram:

• Perimeter of parallelogram = 2 (sum of adjacent sides)
• Area of parallelogram = base × height

Perimeter and Area of the Rhombus:

• Area of rhombus = base × height
• Area of rhombus = 1/2 × length of one diagonal × length of other diagonal
• Perimeter of rhombus = 4 × side

Perimeter and Area of the Trapezium:

● Area of trapezium = 1/2 (sum of parallel sides) × (perpendicular distance between them)
= 1/2 (p₁ + p₂) × h (p₁, p₂ are 2 parallel sides)

Circumference and Area of Circle:

● Circumference of circle = 2πr
= πd
Where, π = 3.14 or π = 22/7
r is the radius of circle
d is the diameter of circle
● Area of circle = πr²

● Area of ring = Area of outer circle – Area of inner circle.

---

Exercise-16 (a)

OP Malhotra Area of Plane Figures Class-9 S.Chand ICSE Maths Ch-16

Question-1

 Find the perimeter and area of the rectangle whose dimensions are

(i) 8 cm by 5 cm

(ii) 12 m by 9 m

(iii) 3.5 m by 2 m

Answer-1

 (i)  Perimeter = 2 (L+B)

Perimeter = 2 (8 + 5) cm

= 26 cm

Area = (8 x 5) cm²

= 40 cm²

(ii)  Perimeter = 2 (L+B)

Perimeter = 2 (12 + 9)

= 42 m

Area = (12 x 9) m²

= 108 m²

(iii) Perimeter = 2 (L+B)

Perimeter = 2 (3.5 + 2) m

= 11 m

Area = (3.5 x 2) m²

= 7 m²

Question-2

Find the Perimeter and area of the square whose each side is

(i) 3 cm

(ii) 5 m

(iii) 1.3 m

(iv) 2.4 m

Answer-2

( Perimeter of squire = 4 x side and Area of squire =  side ² )

(i) Perimeter = ( 4 x 3) = 12 cm

Area = 3² = 9 cm²

(ii) Perimeter = (4 x 5) = 20 cm

Area = 5² = 25 cm²

(iii) Perimeter = (4 x 1.3) m

= 5.2 m

Area = (1.3)² m²

= 1.69 m²

(iv) Perimeter = (4 x 2.4 m)

= 9.6 m

Area = (2.4)² m²

= 5.76 m²

Question-3

Find the length of one side and perimeter of a square whose area is :

(i) 25 m²

(ii) 144 m²

(iii) 256 cm²

(iv) 961 dm²

Answer-3

( side of squire = √ area)

(i) Let, the length of one side = a

∴ a² = 25

a = 5,

∴ Perimeter = (4 x 5)

= 20 m

(ii) a² = 144

a = 12,

Perimeter = (4 x 12)

= 48 m.

(iii) a² = 256

a = 16

Perimeter = 4 x 16 = 64 cm.

(iv) a² = 961

a = 19,

Perimeter = 4 x 19 = 126 dm

Question-4

The perimeter of a rectangle is 30 cm, and its breadth is 6 cm, find its length and area.

Answer-4

Let, length of the rectangle is a,

2 (a + 6) = 30

Or, a + 6 = 15

Or, a = 9

∴ length = 9 cm

Now area is L x B

∴ 9 x 6  = 54 cm2

Question-5

The perimeter of a rectangle is 30 cm, and its breadth is 6 cm, find its length and area.

Answer-5

Let, length of the rectangle is a,

2 (a + 6) = 30

Or, a + 6 = 15

Or, a = 9

∴ length = 9 cm

Let, the breadth is = b

∴ 30 x b = 450

b = 15 m

Question-6

The perimeter of a rectangular field is 3/5 km. If the length of the field is twice its width , fins its area in sq metres.

Answer-6

Let, the width is = x km

∴ length = 2x km

2 (2x + x) = 3/5

Or, 2 x 3x = 3/5

Or, x = 1/10

∴ length = 2/10 = 1/5 km.

∴ Area = 1/10 x 1/5 km²

= (100 x 200) m²

= 20000 m²

Question-7

If the side of a square is doubled, find the ratio of the area of the resulting square to that of the given square.

Answer-7

Let the side of the square is = a

∴ , the side of new squire = 2a

area of original squire = a²

area of new squire = (2a)²

= 4a²

ratio of area of new squire to area of original squire

= 4a² / a²

= 4/1

= 4:1

Question-8

 The side of a square field is 89 m. By how many square metres does its area fall short of a hectre.

Answer-8

Area of the square field is = (89)² m²

= 7921 m²

1  hectre = 10,000 m²

∴ Area short of (10,000 – 7921) m²

= 2079 m²

Question-9

 The side of a square is 25 cm. Find the length of its diagonal correct to 2 decimal places.

Answer-9

Diagonal = √ ( 25²+ 25²  )

=  √ ( 625+ 625  )

=  √ ( 1250 )

= 35.35 cm

Question-10

If the diagonal of a rectangle is 10 cm and its width is 6 cm, find its area.

By the phythogorus theorem,

(10)² = (6)² + Length²

∴ (length)² = 100 – 36 = 64

Length = 8

∴ Area = (8 x 6) cm²

= 48 cm²

Question-11

 The length of a rectangle is twice its width. If the length of its diagonal is 16√5 cm, find its area.

Aswer-11

Let the width is b cm

∴ Length = 2b cm

∴ (2b)² + b² = (16√5)²

5b² = 256 x 5

b² = 256

b = 16

∴ Area = (16 x 32) cm²

= 512 cm²

Question-12

The sides of two squares are in the ratio 2:3. Find the ratio of their perimeters and areas

Answer-12

Let side be 2x and 3x

Perimeter = 4 x side

= 4 x 2x

= 8x

and

Perimeter = 4 x side

= 4 x 3x

= 12x

Ratio of perimeter = 8x / 12x

= 2/3

Now Ratio of area = (2x)² / (3x)²

= 4x² / 9x²

= 4/9
= 4 : 9
Question-13

How many carpets , 3 m by 2 m, are required to cover the floor of  a hall 30 m by 12 m?

Answer-13

Area of the floor = (30 x 12) m²

= 360 m²

Area of the carpet = (3 x 2) m²

= 6 m²

∴ Number of carpet = Area of the floor / Area of the carpet

360 / 6 = 60

Question-14

 A room is 5 m by 4 m. Find the cost of cementing its floor at Rs. 7.50 per m²

Answer-14

Area of the room = (5 x 4) m²

= 20 m²

Cost of cementing = (20 x 7.50) Rs.

= 150 Rs.

Question-15

A room is 12 m by 10 m by 10 m. Find the cost of covering its floor with bricks 20 cm by 6 cm. If the cost of one thousand bricks is Rs. 300

Answer-15

Area of the floor = (12 x 10) m²

= 120 m²

Area of one bricks = (20 x 6) cm²

= 120 m²

∴ Total number of bricks required =Area of the floor  / Area of one bricks

12 x 10000 / 120

= 10000

∴ Total bricks required = 10000,

∴ Cost of 1000 bricks = Rs. 300

∴ Cost of 10,000 bricks = Rs. 3000

Question-16

In exchange for a square plot of land, one of whose sides is 84 m, a man want to buy a rectangular plot 144 m long and of the same area as the square plot. Determine the width of the rectangular plot.

Answer-16

let the width of the rectangular plot.be = x

Given that Area of rectangular plot = area of squire 

L x B = side x side

144 x B = 84 x 84

B = 84 x 84 / 144

B= 49 m

Question-17

A plot 110 metres long and 80 metres broad is to be covered with grass leaving 5 metres all around. Find the area to be laid with grass

Answer-17

Area of to be laid with gram = (110 – 10) (80 – 10) m²

= 100 x 70 m²

= 7000 m²

Question-18

The dimensions of a rectangular field are in the ratio 6:5. Find the cost of constructing a fence around the field at the rate of Rs. 1.25per metre, given that the area of the field is 27000 m².

Answer-18

let the common ratio be x

∴ 6x x 5x = 27000

Or, x² = 27000 / 6 x 5

x= 30

∴ Perimeter = 2 (180 + 150)

= 2 x 330

= 660 m

Cost = (660 x 1.25) Rs.

= 825 Rs.

Question-19

The cost of enclosing a rectangular garden with a fence all round at the rate of 75 paise per metre is Rs. 300. If the length of the garden is 120 metres, find the area of the garden in square metres.

Answer-19

The cost of enclosing= 300 

Rate per meter= 75 paise per metre

= 75/100  = 3/4 Rs /m

Perimeter = 300 / (3/4)

= 400 m

2 (L+B )= P of a rectangular garden

(120 + B) = 400 /2

B= 80 m

Area = L x B

= 120 x 80

= 9600 m²

Question-20

Find the area and perimeter of a square plot of land, the length of whose diagonal is14 metres. Give your answer correct to 2 places of decimals

Answer-20

Let, the length be ‘a’ meter

∴ a² + a² = 196

a² = 98

∴ Area = 98 m²

Perimeter = 4√98 m

= 39.60 m

Question-21

 A lawn 10 m by 8 m is surrounded by a path 1 m wide. Find the area of the 1 m wide. Find the area of path.

Answer-21

Area of the lawn = (10 x 8) m²

= 80 m²

Total area of lawn & Path is = 12 x 10 = 120 m²

∴ Path = (120 – 80) m²

= 40 m²

Question-22

The diagram given below shows two paths drawn inside a rectangular field 50 m long and 35 m wide. Find the area of the shaded portion.

Answer-22

Area of the shaded portion = Area of the rectangle – (Area of the portion without path)

= (50 x 35) – (50 – 5) (35 – 5)

= 50 x 35 – 45 x 30

= (1750 – 1350)

= 400 m²

Question-23

Find the area of the four walls of a room, 7 m long, 5 m broad, and 3 m high. Find the cost of distempering the walls at the rate of Rs. 3.15 per m²

Answer-23

Area of the four wall = 2 (7 x 3 + 5 x 3) m²

= 2 (21 + 15)

= 2 x 36 m²

= 72 m²

Cost of distempering = (72 x3.15) Rs.

= 226.8 Rs.

Question-24

Find the cost of the paper for the walls of the room if each piece of paper is 40 cm wide and 60 cm long : the room is 6 m long, 4 m wide, 3 m high and the cost of paper is Rs. 1.40 per piece; allow 11 m² for doors etc., and assume that a whole number of pieces has to be bought.

Answer-24

Area of each paper = (40 x 60) cm²

= 2400 cm²

Area of walls = 2 x H (L + B)

= 2x 3 (6  + 4 ) m²

= 6 (10) m²

= 60 m²

=  60x 100 x 100 cm²

= 600000 cm²

Area of door = 11 m²

= 11 x 100 x 100 cm²

= 110000 cm²
Remaining are =600000 cm² – 110000 cm²

= 490000 cm²

piece of paper = 490000 cm² / 2400 cm²

= 240.166

= 205

Cost of piece = 205 x 1.40

=287 Rs

Question-25

a cistern 6m long ………..   wet surface.

Answer-25

L= 6m

B=4m

level of water h = 1.25

Area of wet surface =area of 4 wal + area of base

=2 (6+4) x 1.25 + 6 x 4 m²

= 49 m²

Question-26

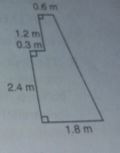
Find the area and perimeter of the shape illustrated in figure given below. The corners are all right angles.

Answer-26

……………………..

Question-27

………………………..

Answer-27

……………………….

Question-28

How many tiles, each 12 cm by 6 cm  are needed for a floor of a room 162 cm long, 144 cm wide?

Answer-28

Area of one tiles = (12 x 6) cm²

= 72 cm²

Area of room = (162 x 144) cm²

∴ Number of tiles = 162 x 144 / 72

= 324 tiles.

Question-29

How many dusters, each 16 cm square can be cut from material 84 cm long, 36 cm wide? What area remains over?

Answer-29

L=84 cm

B = 36 cm

Area = L x B = 84 x 36  cm²

side of duster= 16 cm

area of duster= 16 x 16 cm²

= total number of duster =84 x 36  cm² / 16 x 16 cm²

= 11.8125

= 11 (on whole number)

reaming clothes = (84 x 36) – (11 x 256)

= 3024-2816

=208 cm²

Question-30

 A floor which measures 15 m x 8 m is to be laid with tiles measuring 50 cm x 25 cm. Find the number of tiles required. Further, if a carpet is laid on the floor so that a space of 1 m exists between its edges of the floor, what fraction of the floor is uncovered.

Answer-30

tiles measuring 

$50cm=0.5m$

and $25cm=0.25m$
Tiles along the length of the room=0.515​ = $30$ tiles
Tiles along the length of the room=0.258​ =$32$ tiles
Total number of tiles required =$30\times 32$ =$960$ tiles
To leave $1m$ between the carpet and wall on all sides, the carpet needs to be $2m$ shorter in each dimension.
Therefore,
$(15-2)m(8-2)m$
$=(13\times 6)m$
$=78m²$
Therefore, the room area is $15\times 8$ = $120m²$

 

 

---

Exercise-16 (b)

OP Malhotra Area of Plane Figures Class-9 S.Chand ICSE Maths Ch-16

Question-1

For any triangle, complete the following table

	(i)	(ii)	(iii)	(iv)	(v)	(vi)	(vii)
Base	6	8	5	X	6	?	?
Height	10	14	20	2x	?	5	11
area	?	?	?	?	30	50	110

Answer-1

……………

Question-2

The area of a triangle is 6 cm² and its base is 4 cm. Find its height.

Answer-2

 Area = 6 cm²

Base = 4 cm

6 = ½ x 4 x height

Or, height = 3 cm.

Question-3

 Find the base of a triangle is its

(i) area is 25 ares and height 20 m.

(ii) area is 16 hectares and height 40 decametres

1 are = 100 m²

1 hectare = 10000 m²

1 decameter = 10 m

Answer-3

……………

Question-4

 Find the area of the triangle whose sides are

(i) 26 cm, 28 cm, 30 cm

(ii) 48 cm, 73 cm, 55 cm

(iii) 21 cm, 20 cm, 13 cm

(iv) 7.5 cm, 18 cm, 19.5 cm

Answer-4

(i) a = 26 cm, b = 28 cm, c = 30 cm

S = (a + b + c) / 2

= (26 + 28 + 30) / 2

= 84 / 2

= 42

Area = √42 (42 – 36) (42 – 28) (42 – 30)

= √42 x 16 x 14 x 12

= √112896

= √336

(ii) a = 48 cm, b = 73 cm, c = 55 cm

S = (a + b + c ) / 2

= (48 + 73 + 55 ) / 2

= 176 /2

= 88

∴ Area = √88(88 – 48) (88 – 73) (88 – 55)

= √88 x 40 x 15 x 33 cm²

=√1742400

= 1320 cm²

(iii) a = 21 cm, b = 20 cm, c = 13 cm

S = (a + b + c) / 2

= (21 + 20 + 13) / 2

= 54 / 2

= 27

∴ Area =-√27 (27 – 21) (27 – 20) (27 – 13)

= √27 x 6 x 7 x 14

= √15876

= 126

(iv)

a = 7.5 cm, b = 18 cm, c = 19.5 cm

S = (a + b + c) / 2

= (7.5+1.8+19.5 ) / 2

= 45 / 2

= 22.5

∴ Area =-√22.5 (22.5 – 7.5) (22.5 – 18) (22.5 – 19.5)

= √22.5 (15) (4.5) (3)

= √4556.25

= 67.5 cm²

Question-5

The perimeter of a triangle is 540 m and its sides are in the ration 25 : 17 : 12. Find the area of the triangle.

Answer-5

Let, the sides of the triangular = 25x, 17x, 12x

Perimeter = (25x + 17x + 12x)

= 54x

The perimeter of a triangle is 540 m given

∴ 54x = 540

x = 10

∴ Sides are = 250, 170, 120

a = 250 cm, b =  170 cm, c =120 cm

S = (a + b + c) / 2

= (250+ 170+ 120 ) / 2

= 540 / 2

= 270

∴ Area =-√270 (270 – 250) (270 – 170) (270 – 120)

= √270 (20) (100) (150)

= √81000000

= 9000 m²

Question-6

 The given figure, ABCD represents a square of side  6 cm. F is a point on DC such that the area of the triangle ADF is one third of the area of the square. Find the length of FD.

Answer-6

Area of square = 6 x 6 = 36 cm²

Area of ΔADF = 1/3 x 36 = 12 cm²

∴ ½ x DF x 6 = 12

DF = 4 cm

Question-7

Find the area of a triangle with base 5 cm and whose height is equal to that of a rectangle with base 5 cm and area 20 cm²

Answer-7

Let, l be the length of the rectangle,

∴ l x 5 = 20

l = 4

∴ Area of triangle = ½ x 5 x 4

= 10 cm²

Question-8

Answer true or false:

(i) The area of a triangle with base 4 cm and perp. Height 6 cm is 24 cm²

(ii) The area of a triangle with sides measuring, a, b, c, is given by √s(s – a) (s – b) (s – c) where s is the perimeter of the triangle.

(iii) The area of a rectangle and a triangle are equal if they stand on the same base and are between the same parallels.

Answer-8

(i) base = 4 cm, height = 6 cm

Area = ½ x 4 x 6

= 12 cm²

False

(ii) False

S is semi-perimeter not perimeter.

(iii) False,

Area of triangle = ½ x Area of rectangle.

Qustion-9

ABC is triangle in which AB = AC = 4 cm and ∠A = 90^o, calculate the area of ΔABC.

Answer-9

∴ Area of ΔABC = 1/2( base x height)

∴ Area of ΔABC = 1/2( 4 x 4)

= 8 cm²

Question-10

the side of triangle field are 320 m 200m and 180 m long……. in m²

Answer-10

on reducing 50 : 1

side will be = 320/50 m = 6.4

 200 /50 m =4

and 180 /50 m=3.6

area = 1/2 ( base x height)

area = 1/2 ( 320 x 102.5)

=16400 m²

Question-11

The sides of a triangular field are 975 m, 1050 m and 1125 m . If this field is sold at the rate of Rs. 1000 per hectare, find its selling price.

Answer-11

Area of triangular field=√s*(s-a)*(s-b)*(s-c). [heron’s formula]
a,b,c are the sides of triangle.
s=975+1050+1125/2=1575
Area of triangular field=√1575*(1575-975)*(1575-1050)*(1575-1125)
area=√1575*600*525*450
area=√945000*236250
area=√223256250000
area=472500 m²
1 hectare = 10000 m²
Therefore, 472500m²=47.25 hectares
Selling price = 47.25*1000
Selling price= Rs.47250

Question-12

Find the area of the equilateral triangle whose each side is (i) 12 cm  (ii) 5 cm

Answer-12

 (i) 12 cm 

sides=12 cm

We know that

area of equilateral triangle

 (ii) 5 cm

Side of equilateral triangle = 5 cm

Area =√3a² /4

= √3(5)² / 4

= 25 x 1.73 /4

= 10.8 cm²

Question-13

 The perimeter of an equilateral triangle is 24 cm. Find its area.

Answer-13

Let ‘a’ be the side of the equilateral triangle,

3a = 24

a = 8

Area = √3/4 x 8²

= √3/4 x 64

= 16√3

= 27.712 cm²

Question-14

The perimeter of an equilateral triangle is √3 times its area. Find the length of each side.

Answer-14

Let, a be the length of each side,

Perimeter = √3 x area

3a = √3 x √3/4 a²

Or, a = 4

∴ length = 4 unit.

Question-15

 The area of an equilateral triangle is 173.2 m². Find its perimeter.

Answer-15

 Let, a be the side

√3/4 a² = 173.2

Or, a² = 173.2 x 4 / √3

a =20 m

Perimeter = 3 x 20 = 60 m

Question-16

Find the area of the isosceles triangle whose

(i) each of the equal sides is 8 cm  and the base is 9 cm

(ii) each of the equal sides is 10 cm and the base is 12 cm

(iii) each of the equal sides is 7.4  cm and the base is 6.2 cm;

(iv) Perimeter is 11 cm and  base is 4 cm.

Answer-16

(i) each of the equal sides is 8 cm  and the base is 9 cm

Semi-perimeter =( a + b + c )/ 2
                         = (8 + 8 + 9)/2
                         = 25/2
                         = 12.5 

Area of triangle = √ s (s-a) (s-b) (s-c)
                         = √ 12.5 (12.5 – 8) (12.5-8) (12.5-9)
                         = √ 12.5 x 4.5 x 4.5 x 3.5
                         = √ 885.9375
                         =  29.77

So, 29.77 is the area of triangle.

(ii) each of the equal sides is 10 cm and the base is 12 cm

Since we have given that

Measure of equal sides = 10 cm

Measure of third side = 12 cm

so, we need to find the area of an isosceles triangle.

Semi perimeter s = 

So, Area of isosceles triangle would be

Area of triangle = √ s (s-a) (s-b) (s-c)
                         = √ 16 (16 – 10) (16-10) (16-12)
                         = √ 16 x 6 x 6 x 4
                         = √ 2304
                         =  48 cm²

(iii) each of the equal sides is 7.4 cm and the

base is 6.2 cm;

= Area of isosceles = 1/2×b×h.

= 1/2×6.2×7.4.

= [ 7.4 divide by 2].

= 1×6.2×3.7.

= 22.94.

(iv) perimeter is 11 cm and base is 4 cm.

= Area of isosceles = 1/2×b×h.

= 1/2×4×11.

= 2×11.

= 22.

Question-17

 (i) The base of an isosceles triangle is 24 cm and its area is 192 sq. cm. Find its perimeter.

(ii) Find the base of an isosceles triangle whose area is 12 cm² and one of the equal sides is 5 cm.

 Answer-17

(i)

In ΔABC

AB = AC since the given triangle is isosceles.

Base = BC = 24 cm

Altitude = AD

Area = 192 sq.cm.

Area of triangle = 1/2 (base x height)

So,

Thus AB =AC = 20 cm

BC = 24 cm

Perimeter of triangle = Sum of all sides

= AB+BC+AC

= 20+24+20

= 64 cm.

Hence the perimeter of triangle is 64 cm

(ii)

Area: 12 cm sq

side = 5 cm ²

………………………

Question-18

The perimeter of an isosceles triangle is 42 cm. Its base is 2/3 times the sum of equal sides. Find the length of each side and the area of the triangle.

Answer-18

let each of the equal sides be x
let the base by y
y = (2/3)(2x) = 4x/3

so x + x + (4/3)x = 42
multiply by 3
3x + 3x + 4x = 126
10x = 126
x = 12.6
so the base = (4/3)(12.6) = 16.8

use Pythagoras to find the height, h
h^2 + 8.4^2 = 12.6^
h^2 = 88.2
h √88.2

Area = (1/2)base x height
= (1/2)(16.8)√88.2
= appr. 78.888

Question-19

PQR is an isosceles triangle whose equal sides PQ and PR are 13 cm each, and the base QR measures 10 cm. PS is the perpendicular from P to QR and O is a point on PS such that ∠QOR = 90⁰. Find the area of shaded region

Answer-19

……………….

Question-20

The perimeter of a right triangle is 50 cm and the hypotenuse is 18 cm. Find its area.

Answer-20

Perimeter = 50cm

Hypotenuse = 18 cm.

Let the sides be a b and c where c is Hypotenuse.

Now a + b + c = 50

a + b = 50 – c

A^ +b^ = c^

(a+ b) ^2 = (50 – c) ^2

A^2 + b^2 + 2ab = 2500 – 100c + c^2

C^2 + 2ab = 2500 – 100 ☓ 18 +c^2

2ab = 2500 – 1800

2ab = 700

ab = 350

Area of triangle = 1/2 ☓ base ☓ height

Area = 1/2 ☓ a ☓ b

Area = 1/2 ☓ 350

Area = 175 cm^2

 

---

Exercise-16 (c)

 Area of Plane Figures Class-9 S.Chand ICSE Maths Ch-16

Question-1

 Find the area of a parallelogram whose base and height are as given below:

	(i)	(ii)	(iii)	(iv)
Base	8 cm	2.8 cm	12 mm	6.5 m
Height	3 cm	5 cm	8.7 mm	4.8 m

Answer-1

Area of  parallelogram = Base x height

(i) Area = = 8 x 3 cm²

= 24 cm²

(ii) Area = (2.8 x 5) cm²

= 14 cm²

(iii) Area = 12 x 8.7 mm²

= 104.4 mm²

(iv) Area = (6.5 x 4.8) m²

= 31.20 m²

Question-2

The area of a parallelogram is 1 ½ ares. Its base is 20 m. Find its height. (1 arc = 100 m²)

Answer-2

Area = (3/2 x 100) m

= ( 3 x 50) m²

= 150 m²

∴ 150 = 20 x h

h = 7.5 m

Question-3

 In a parallelogram ABCD, AB = 8 cm, BC = 5 cm, perp. From A to DC = 3 cm. Find the length of the perp. drawn from B to AD.

Answer-3

 

………………….

Question-4

 A parallelogram has side 34 cm and 20 cm. One of its diagonals is 42 cm. Calculate its area.

Answer-4

At first we have to calculate the area of the triangle having sides 34cm, 20cm and 42cm.
Now,

s = (34+20+42) /2
= 48 cm
∴ Area of triangle
= √48(48-34)(48-20)(48-42)
= √48×14×28×6
= √4×12×2×7×4×7×2×3
= √ 4×4×2×2×7×7×36
= 4 x 2 x 7 x 6
= 336cm²
∴ Area of parallelogram
= 2 x Area of triangle if separating boundary of diagonal
= 2 x 336
= 672cm².

Question-5

ABCD is a parallelogram with side AB = 12 cm. Its diagonals AC and BD are the lengths 20 cm and 16 cm respectively. Find the area of || gm ABCD

Answer-5

Let O be the intersecting point of AC and BD

We know,

diagonals of a parallelogram bisect each other

OA =OC = (1/2)×AC = 10cm

OB = OD= (1/2 )×BD = 8cm

in ∆AOB

OA=10cm

OB=8cm

AB=12cm

By using Heron’s formula

ar(∆AOB)=√s(s-a)(s-b)(s-c)

s=(a+b+c)/2

=(12+8+10)/2=

30/2=15cm

ar(∆AOB)=√15×3×7×5

= 15√7 cm²

we know that the diagonals of a parallelogram divides it into four equal triangles

=>ar(∆AOB)=ar(∆BOC)=ar(∆COD)=ar(∆AOD)= 15√7 cm²

ar(ABCD) = 4*15√7 = 60√7 cm² (Ans.)

Question-6

What is the area of a rhombus which has diagonals of 8 cm and 10 cm.

Answer-6

 Area of rhombus = ½ x 8 x 10 cm²

= 40 cm²

Question-7

The area of a rhombus is 98 cm². If one of its diagonals is 14 cm, what is the length of the other diagonal?

Answer-7

Let other diagonal be =  a

Area of rhombus = ½ x Product of diagonals

98 = ½ x 14 x a

Or, a = 14 cm

Question-8

 PQRS is a rhombus.

(i) If it is given that PQ = 3 cm, calculate the perimeter of PQRS

(ii) If the height of the rhombus is 2.5 cm, calculate its area,

(iii) The diagonals of a rhombus are 8 cm and 6 cm respectively. Find its perimeter.

Answer-8

(i)

since all sides of rhombus are same in length

Therefore, perimeter of Rhombus PQRS is = 4× length of one side

= 4× 3= 12c.m

(ii) 

Area of rhombus = base x height

= 3 x 2.5

=7.5 cm²

(iii) 

PQRS is a rhombus and we know that all four sides of a rhombus are of equal length.

And, In Δ POQ

PQ is hypotenuse, OP is base and OQ is perpendicular.

Using Pythagoras Theorem –

⇒ (PQ)² = (OP)² + (OQ)²

⇒ (PQ)² = (3)² + (4)²

⇒ (PQ)² = 9 + 16

⇒ (PQ)² = 25

⇒ PQ = √25

⇒ PQ = 5 cm

So, length of each side of the given rhombus is 5 cm.

Perimeter of rhombus = 4 × side

⇒ 4 × 5

= 20 cm

So, perimeter of the rhombus PQRS is 20 cm.

Question-9

The sides of a rhombus are 5 cm each and one diagonal is 8 cm, calculate,

(i) The length of the other diagonal and

(ii) The area of the rhombus.

Answer-9

Diagonals bisect each other and they are perpendicular in rhombus

Question-10

In the given figure, ABCX is a rhombus of side 5 cm. angles BAD and ADC are right angles. If DC = 8 cm, calculate the area of ABCX.

Answer-10

In fig.
Angle BAD = Angle ADC
But they’re co interior angles. Thus, AB || CD.
Also, AX || BC, this implies, ABCX is a parallelogram.
Therefore, AB = CX = 5 cm (opposite sides of parallelogram are equal)
Also, AX = BC = 5 cm
Now, DX = DC-CX = 8-5 = 3 cm

In ∆ADX, using Pythagorean theorem, we get,
AD = 4 cm

 

Exercise-16 (d)

OP Malhotra Area of Plane Figures Class-9 S.Chand ICSE Maths Ch-16

Question-1

Find the area of the trapezium if the:

(i) Parallel sides are 3 cm and 6 cm and perp. distance between them is 10 cm.

(ii) Parallel sides are 25 m and 33 m and perp. distance between them is 20 m.

Answer-1

(i) Area of the trapezium = ½ x (3 + 6) x 10 cm²

= 9 x 10 / 2 cm²

= 45 cm²

(ii) Area of the trapezium = ½ x (25 + 33) x 20 m²

= 580 m²

Question-2

The area of a trapezium is 240 m² and the sum of the parallel sides is 48 m. Find the height.

Answer-2

Let, ‘h’ be the height of the trapezium

1/2 x 48 x h = 240

Or, h = 10 m

Question-3

The parallel sides of a trapezium are 4.36 cm and 3.18 cm and area is 18.85 cm². Find the distance between the parallel sides.

Answer-3

Let ‘h’ be the distance between the parallel side,

(1/2) x (4.36 + 3.18) x h = 18.85

Or, 7.54 x h = 37.70

Or, h = 37.7 / 7.54

= 5 cm

Question-4

The area of a trapezium is 475 cm² and the height is 19 cm. Find its two parallel sides if one side is 4 cm greater than the other.

Answer-4

Let, one side is = x cm

another side is = (x + 4) cm

∴ 1/2 x 19 x (2x + 4) = 475

2x + 4 = 50

2x = 46

x = 23

So, two parallel sides are 23 cm, 27 cm cm.

Question-5

The parallel sides of a trapezium are in the ratio 2:5 and the distance between the parallel sides is 10 cm. if the area of the trapezium is 350 cm², find the lengths of its parallel sides.

Answer-5

Let, the common ratio be x

So, sides of the trapezium are 2x and 5x

∴ ½ x 10 x 7x = 350

Or, x = 10

So, lengths of parallel sides are = 20 cm and 50 cm.

Question-6

 In the given figure, AD = BC = 5 cm, AB = 7 cm. The parallel sides AB, DC are 4 cm apart DC =  cm. Find x and the area of the trapezium ABCD.

Answer-6

ABCD is a trapezium in which AB = 7 cm,

AD = BC = 5 cm ,

DC = x cm,

AB // DC ,

Distance between AB and DC is 4 cm

To find :

Value of x = ?

In ∆BFC ,  ∠BFC = 90°,

BC² = BF² + FC² ( using Phythagorean theorem )

=> 5² = 4² + FC²

=> FC² = 5² – 4²

=> FC² = 25 – 16 = 9

=> FC = √9 = √3² = 3 cm

=> DC = DE + EF + FC

=> DC = 3 + 7 + 3 = 13 cm

Now

Area = 1/2 (sum of // side ) x h

= 1/2 (7+13 ) x 4

= 1/2〈 20 x 4 〉

= 40 cm²

Question-7

The parallel sides of a trapezium are 7.5 cm, 3.9 cm, and the other sides are each 2.6 cm. Find its area.

Answer-7

the parallel sides of a trapezium are 7.5cm and 3.9cm

other sides are each 2.6cm

=> isosceles trapezium

if we draw perpendicular from vertex of 3.9 cm side to 7.5 cm side

distance between Perpendicular Drawn & nearest vertex of 7.5 cm  would be

= (7.5 – 3.9) /2

= 1.8 cm

Perpendicular height Would be = √ 2.6² – 1.8²

= √3.52

= 1.876 cm

Area of Trapezium= (1/2)(7.5 + 3.9)(1.876)

= 10.69 cm²

Question-8

given figure show cross section of a concrete structure with measurement given below  calculate area of cross section

Answer-8

……………………………….

Question-9

In the figure find:

(i) AB

(ii) area of the trapezium ABCD.

Answer-9

(i) DC² = DE² + EC²

(10)² = 6² + EC²

EC² = 100 – 36 = 64

EC = 8

∴ AB = 8 cm

(ii) Area = ½ x (8 + 2) x 8

= 4 x 10

= 40 cm²

Question-10

The cross-section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the figure. AM = BN; AB = 4.4 m; CD = 3 m. The height of the tunnel is 2.4 m. The tunnel is 50 m long.

Calculate:

(i) the cost of painting the internal surface of the tunnel (excluding the floor) at the rate of Rs. 5 per m²

(ii) the cost of paving the floor at the rate of Rs. 18 per m²

Answer-10

The cross-section of a tunnel is of the trapezium-shaped ABCD in which  AB = 7 m, CD = 5 m and AM = BN. The height is 2.4 m and its length is 40 m.

(i) AM = BN =(7-5 )/2 = 2/2=1m

∴ In ΔADM,

AD² = AM² + DM²      …[ Using pythsgor as theorem ]
= 1² + (2 . 4)² 
= 1  + 5.76
= 6.67
= (2.6)² 
AD  = 2.6 m

Perimeter of the cross- section of the tunnel = ( 7+ 2.6 + 2.6 + 5 ) m = 17.2 m

Length = 40 m

∴ The internal surface area of the tunnel ( except the floor )

= ( 17.2 x 40 – 40 x 7) m²
= ( 688 – 280 ) m²
= 408 m² 

Rate of painting = Rs. 5 per m²
Hence, total cost of painting = Rs. 5 x  408 = Rs. 1632

(ii) Area of floor of tunnel = l x b = 40 x 7 = 280 m²

Rate of cost of paving = Rs. 18 per m² 

Total cost = 280 x 18 = Rs. 5040

 

………………………

 

---

Chapter Test

Area of Plane Figures Class-9 S.Chand ICSE Maths Ch-16