OP Malhotra Bayes Theorem ISC Class-12 Maths Solutions Ch-19

OP Malhotra Bayes Theorem ISC Class-12 Maths Solutions Ch-19. Step by step Solutions of OP Malhotra SK Gupta, Anubhuti Gangal S.Chand ISC Class-12 Mathematics with Exe-19 and Self Revision. Visit official Website CISCE for detail information about ISC Board Class-12 Mathematics.

OP Malhotra Bayes Theorem ISC Class-12 Maths Solutions Ch-19

Class:	12th
Subject:	Mathematics
Chapter :	Ch-19 Bayes Theorem of Section -A

Board	ISC
Writer	OP Malhotra, SK Gupta, Anubhuti Gangal
Publications	S.Chand Publications 2020-21

-: Included Topics :-

Exe-19

Self Revision

OP Malhotra Bayes Theorem ISC Class-12 Maths Solutions Ch-19

Bayes Theorem Statement :-

Let E₁, E₂,…,E_n be a set of events associated with a sample space S, where all the events E₁, E₂,…, E_n have nonzero probability of occurrence and they form a partition of S. Let A be any event associated with S, then according to Bayes theorem,

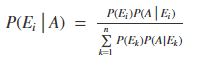
for any k = 1, 2, 3, …., n

Bayes Theorem Formula :-

If A and B are two events, then the formula for Bayes theorem is given by:

P(A|B) = P(A∩B)/P(B)

Where P(A|B) is the probability of condition when event A is occurring while event B has already occurred.

P(A ∩ B) is the probability of event A and event B

P(B) is the probability of event B

Bayes Theorem Derivation :-

Bayes Theorem can be derived for events and random variables separately using the definition of conditional probability and density.

From the definition of conditional probability, Bayes theorem can be derived for events as given below:

P(A|B) = P(A ⋂ B)/ P(B), where P(B) ≠ 0

P(B|A) = P(B ⋂ A)/ P(A), where P(A) ≠ 0

Here, the joint probability P(A ⋂ B) of both events A and B being true such that,

P(B ⋂ A) = P(A ⋂ B)

P(A ⋂ B) = P(A | B) P(B) = P(B | A) P(A)

P(A|B) = [P(B|A) P(A)]/ P(B), where P(B) ≠ 0

Formula for Bayes theorem :-

The formula for Bayes theorem is:
P(A|B)= [P(B|A). P(A)]/P(B)
Where P(A) and P(B) are the probabilities of events A and B.
P(A|B) is the probability of event A given B
P(B|A) is the probability of event B given A.

Exe-19