OP Malhotra Class-11 Binomial Theorem S.Chand ISC Maths Solutions Chapter-13. Step by step Solutions of OP Malhotra S.Chand ISC Class-11 Mathematics with Exe-13 (a), 13 (b), With Chapter Test. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.
OP Malhotra Class-11 Binomial Theorem S.Chand ISC Maths Solutions
| Class: | 11th |
| Subject: | Mathematics |
| Chapter : | Ch-13 Binomial Theorem of Section -A |
| Board | ISC |
| Writer | OP Malhotra |
| Publications | S.Chand Publications 2020-21 |
-: Select Topics :-
OP Malhotra Class-11 Binomial Theorem S.Chand ISC Maths Solutions
Introduction to the Binomial Theorem
The Binomial Theorem is the method of expanding an expression which has been raised to any finite power. A binomial Theorem is a powerful tool of expansion, which has application in Algebra, probability, etc.
Binomial Expression: A binomial expression is an algebraic expression which contains two dissimilar terms. Ex: a + b, a3 + b3, etc.
Binomial Expansions and Series
The binomial formula in statistics is mostly used for counting and for calculating probabilities in experiments. A very similar technique, called binomial series expansion, is used in calculus for rewriting complicated functions into a simpler (binomial) form
Binomial theorem
Binomial theorem, statement that for any positive integer n, the nth power of the sum of two numbers a and b may be expressed as the sum of n + 1 terms of the form
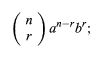
The theorem is useful in algebra as well as for determining permutations and combinations and probabilities. For positive integer exponents, n, the theorem was known to Islamic and Chinese mathematicians of the late medieval period.
Binomial Expansion
Important points to remember:
- The total number of terms in the expansion of (x+y)n are (n+1)
- The sum of exponents of x and y is always n.
- nC0, nC1, nC2, … .., nCn are called binomial coefficients and also represented by C0, C1, C2, ….., Cn
- The binomial coefficients which are equidistant from the beginning and from the ending are equal i.e. nC0 = nCn, nC1 = nCn-1 , nC2 = nCn-2 ,….. etc.
Some Important Observations from the Binomial Theorem
The total number of terms in the binomial expansion of (a + b)n is n + 1.
The sum of the indices of a and b in each term is n.
The coefficient of terms equidistant from the beginning and the end are equal. These coefficients are known as the binomial coefficient and
nCr = nCn-r, r = 0, 1, 2, 3,…, n
The values of the binomial coefficient steadily increase to a maximum and then steadily decrease.
The coefficient of xr in the expansion of (1 + x)n is nCr.
In the binomial expansion (a + b)n, the rth term from the end is (n – r + 2)th term from the beginning.
Exe-13 (a)
OP Malhotra Class-11 Binomial Theorem S.Chand ISC Maths Solutions
Page 13-7 to 13-8
Question 1:
What is number of terms in the each expression of following:
……………….
Question 2:
Write out the expansions of the following.
Question 3:
……………………
……………………
……………………
Question 16:
In the binomial expansion of ……………………… contain Irrational expression .
Exe-13 (b)
OP Malhotra Class-11 Binomial Theorem S.Chand ISC Maths Solutions
Page 13-11 to 13-12
Question 1:
Find the specified terms of the expression in each of the binomials.
………………….
Question 2:
Find the terms independent of x in the expansion of following binomial.
………………….
Question 3:
……………………
……………………
…………………..
Question 19:
In the expansion of ………………………. sixth terms of expansion.
Question 20:
The coefficient of xn in the expansion of (1 + x)(1 – x)n is
(a) …………….
………………….
Chapter Test
OP Malhotra Class-11 Binomial Theorem S.Chand ISC Maths Solutions
Page 13-15 to 13-1
-: End of Binomial Theorem Solution :-
Return to :- OP Malhotra S. Chand ISC Class-11 Maths Solutions
Thanks
Please share with your friends


Sir plz update kijye koi bhi chapter nhi khul Raha hai sir plz I request you ..mera exam h March k end m
ok
Why is it showing that the content is protected
not protected but solutions removed but upload again soon