Pythagoras Theorems Class 9 OP Malhotra Exe-10B ICSE Maths Solutions Ch-10. We Provide Step by Step Solutions / Answer of Questions as latest edition. Visit official Website CISCE for detail information about ICSE Board Class-9 Mathematics.
Pythagoras Theorems Class 9 OP Malhotra Exe-10B ICSE Maths Solutions Ch-10
| Board | ICSE |
| Publications | S Chand |
| Subject | Maths |
| Class | 9th |
| Chapter-10 | Pythagoras Theorems |
| Writer | OP Malhotra |
| Exe-10A | Tough Proving Questions on Pythagoras Theorems |
| Edition | 2025-2026 |
Complex Questions on Pythagoras Theorems
Que-1: ABCD is a square, prove that AC² = 2AB².
Sol: Given : ABCD is a square in which AC is its diagonal

In ∆ABC, ∠B = 90°
∴ AC² = AB² + BC² (Pythagoras Theorem)
= (AB)² + (AB)²
{∵ AB = BC sides of the square}
= 2Ab²
Hence AC² = 2AB²
Que-2: In the figure, AB = BC = CA = 2a and segment AD ⊥ side BC. Draw that
(i) AD = a√3
(ii) area of ∆ABC = a²√3
Sol: Given : In ∆ABC,
AB = BC = CA = 2a
AD ⊥ BC

(i) ∵ The sides of ∆ABC are equal (each = 2d)
∴ It is an equilateral triangle
∴ AD bisects BC at D
i.e. BD = DC = a
Now in right ∆ABD
AB² = AD² + BD² (Pythagoras Theorem)
⇒ (2a)² = AD² + (a)²
⇒ 4a² = AD² + a²
⇒ AD² = 4a² – a²
⇒ AD² = 3a²
⇒ AD = √3
Hence AD = a
(ii) Now area of ∆ABC = (1/2) base x altitude
= (1/2) BC x AD
= 12 (2a) (√3a)
= √3 a² = a²√3
Hence proved.
Que-3: In the figure, prove that Ab² – AD² = CD² – CB².
Sol: Given : In quadrilateral ABCD,
∠B = 90° and ∠D = 90°
To prove : Ab² – AD² = CD² – CB²
Construction : Join AC
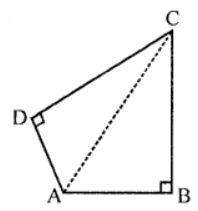
In right ∆ABC, ∠B = 90°
∴ AC² = AB² + BC² … (i)
(Pythagoras Theorem) Similarly in right ∆ADC,
AC² = AD² + CD² … (ii)
From (i) and (ii),
AB² + BC² = AD² + CD²
⇒ AB² – AD² = CD² – BC²
⇒ AB² – AD² = CD² – CB²
Hence proved.
Que-4: In a ∆ABC, AD ⊥ BC. Prove that AB² + CD² = AC² + BD².
Sol: Given : In ∆ABC, AD ⊥ BC
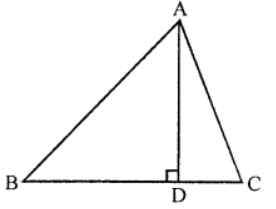
In right ∆ABD (∵ AD ⊥ BC)
AB² = BD² + AD² (Pythagoras Theorem)
⇒ AD² = AB² – BD² … (i)
Similarly in right ∆ACD
AC² = AD² + CD²
⇒ AD² = AC² – CD² … (ii)
From (i) and (ii),
AB² – BD² = AC² – CD²
∴ AB² + CD² = AC² + BD²
Hence proved.
Que-5: In a quadrilateral ABCD, the diagonals AC, BD intersect at right angles. Prove that Ab² + CD² = BC² + DA²
Sol: Given: In quadrilateral ABCD, diagonals AC and BD intersect each other at right angles at O
In right ∆ABO,
AB² = AO² + BO² (Pythagoras Theorem)
Similarly in right ∆BOC,
BC² = BO² + CO²
In right ∆COD
CD² = CO² + DO²
and in right ∆AOD
DA² = AO² + DO²
Now AB² + CD² = AD² + BO² + CO² + DO² … (i)
and BC² + DA² = BO² + CO² + AO² + DO²
= AO² + BO² + CO² + DO² … (ii)
From (i) and (ii),
AB² + CD² = BC² + DA²
Hence proved.
Que-6: In ∆ABC, ∠B = 90° and D is mid-point of BC. Prove that
(i) AC² = AD² + 3CD²
(ii) BC² = 4 (AD² – AB²)
Sol: Given : In ∆ABC, ∠B = 90°
D is mid-point of BC
AD is joined

In right ∆ABD,
AD² = AB² + BD² (Pythagoras Theorem)
⇒ AD² = AB² + ((1/2) BC)² (∵ D is mid-point of BC)
⇒ AD² = AB² + BC²/4
⇒ 4AD² = 4AB² + BC²
∴ BC² = 4AD² – 4AB² = 4 (AD² – AB²)
(i) and in right ∆ABC
(ii) AC² = AB² + BC²
= AB² + (2CD)² (∵D is mid-point of BC)
= AB² + 4CD²
= (AD² – BD²) + 4CD² {∵ AD² = AB² + BD²}
= AD² – CD² + 4CD² (∵ BD = CD)
= AD² + 3CD²
Hence proved.
Que-7: The side BC of a square ABCD is produced to any point E. Prove that AE² = 2BC. BE + CE².
Sol: Given : ABCD is a square whose side BC is produced to E
EA is joined
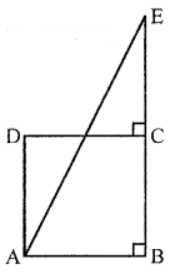
In right ∆ABE
AE² = AB² + BE² = AB² + (BC + CE)²
= AB² + BC² + CE² + 2BC.CE
= BC² + BC² + CE² + 2BC (BE – BC)
= 2BC² + CE² + 2BC.BE – 2BC²
= 2BC.BE + CE²
Hence proved.
Que-8: ABCD is a rhombus. Prove that AC² + BD² = 4AB².
Sol: Given : In rhombus ABCD, diagonals AC and BD bisect each other at right angle at O
In right ∆AOB, ∠AOB = 90°
∴ AB² = AO² + OB²
⇒ AB² = ((1/2) AC)² + ((1/2) BD)²
⇒ AB² = (1/4) AC² + (1/4) BD²
⇒ 4AB² = AC² + BD²
Hence AC² + BD² = 4AB²
Hence proved.
Que-9: In the figure, ∠B of ∆ABC is an acute angle and AD ⊥ BC. Prove that
AC² = AB² + BC² – 2BC.BD
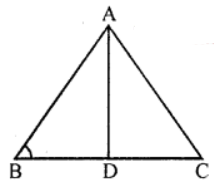
Sol: Given : In ∆ABC, ∠B is an acute angle AD ⊥ BC
To prove : AC² = AB² + BC² – 2BC.BD
Proof: In right ∆ABD
AB² = AD² + BD² (Pythagoras Theorem)
⇒ AD² = AB² – BD² … (i)
Similarly in ∆ADC
AC² = AD² + DC²
= AB² – BD² + (BC – BD)²
= AB² – BD² + BC² + BD² – 2BC.BD
= AB² + BC² – 2BC.BD
Hence proved.
Que-10: In a quadrilateral ∆BCD, ∠B = 90° and AD² = AB² + BC² + CD². Prove that ∠ACD = 90°.
Sol: Given : In quadrilateral ABCD, ∠B = 90° and AD² = AB² + BC² + CD²
In right ∆ABC
AC² = AB² + Bc² … (i)
(Pythagoras Theorem)
∵ AD² = AB² + BC² + CD² (given)
AD² = AC² + CD² [From (i)]
∴ In ∆ACD,
∠ACD = 90°
(Converse of Pythagoras Theorem)
Hence proved.
Que-11: ABC is a triangle right angled at A and p is the length of the perpendicular from A on BC. Show that
(i) pa = bc Hence deduce that
(ii) 1/p2² = 1/b² + 1/c²
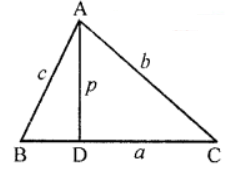
Sol: Given : In ∆ABC, ∠A = 90°
AD ⊥ BC
AD = p, AB = c, BC = a and AC = b
In right ∆ABC, ∠A = 90°
∴ BC² = AB² + AC² (Pythagoras Theorem)
a² = c² + b² = b² + c² …. (i)
(i) Area of ∆ABC = 12 base x altitude
= (1/2) BC x AD
= (1/2) ap
and also area of ∆ABC = (1/2) AB x AC
= (1/2) c.b
∴ (1/2) pa = (1/2) bc
⇒ Pa = bc
(ii) ∵ pa = bc
Squaring both sides,
p²a² = b²c²
p² (b² + c²) = b²c² [from (i)]
p² = (b²c²)/(b²+c²)
⇒ 1/p² = (b²+c²)/b²c²
⇒ 1/p² = {b²/(b²c²)} + {c²/(b²c²)}
⇒ 1/p² = 1/c² + 1/b²
Hence proved.
Que-12: In the given figure, ∠B is acute and segment
AD ⊥ side BC. Show that
(i) b² = h² + a² + x² – 2ax
(ii) b² = a² + c² – 2ax
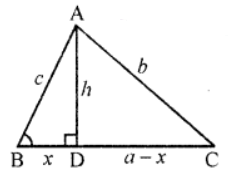
Sol: (i) b² – h² + a² + x² – 2ax
(ii) b² = a² + c² – 2ax
Proof: In right ∆ABD
AB² = AD² + BD² (Pythagoras Theorem)
⇒ c² = h² + x² … (i)
(ii) b² = a² + h² + x² – 2ax
= a² + c² – 2ax [From (i)]
∴ b² = a² + c² – 2ax
Hence proved.
— : End of Pythagoras Theorems Class 9 OP Malhotra Exe-10B ICSE Maths Ch-10.–
Return to :– OP Malhotra S Chand Solutions for ICSE Class-9 Maths
Thanks
Please Share with Your Friends


