Quadratic Equations Class 11 OP Malhotra Exe-10A ISC Maths Solutions Ch-10 Solutions. In this article you would learn about Quadratic Equation and Theorem and its Formulae. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Quadratic Equations Class 11 OP Malhotra Exe-10A ISC Maths Solutions Ch-10
| Board | ISC |
| Publications | S Chand |
| Subject | Maths |
| Class | 11th |
| Chapter-10 | Quadratic equations |
| Writer | O.P. Malhotra |
| Exe-10(A) | Quadratic Equation and Theorem and its Formulae. |
Exercise- 10A
Quadratic Equations Class 11 OP Malhotra Exe-10A Solution.
Find the roots of the following equations.
Que-1: 2x² + x – 3 = 0
Sol: Given 2x² + x – 3 = 0
On comparing with ax² + bx + c = 0, we have
a = 2 ; 4 = 1 and c = – 3
Then by quadratic formula, we have
x = {−b±√(b²-4ac)}/2a
= {−1±√{1-4×2×(-3)}}/(2×2) = (−1±5)/4
⇒ x = –6/4, 1
⇒ x = –3/2, 1
Que-2: 6x² + 7x – 20 = 0
Sol: Given 6x² + 7x – 20 = 0
On comparing with ax² + bx + c = 0, we have
a = 6; b = 7 and c = – 20
∴ x = {−b±√(b²-4ac)}/2a
= {−7±√{7²-4×6×(-20)}}/(2×6)
= (−7±√(49+480)}/12
= (−7±23)/12 = −30/12, 16/12
⇒ x = –15/6, 4/3 i.e. x = – 5/2, 4/3
Que-3: 36x² + 23 = 60x
Sol: Given 36x² – 60x + 23 = 0
On comparing with ax² + bx + c = 0 ; we have
a = 36 ; b = – 60 ; c = 23
Then using quadratic formula,
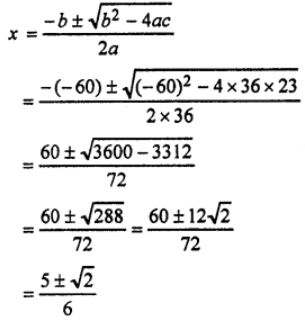
Que-4: x² – 2x + 5 = 0
Sol: Given x² – 2x + 5 = 0
On comparing with ax² + bx + c = 0, we have
a = 1 ; b = – 2 and c = 5
Then by quadratic formula, we have
∴ x = {−b±√(b²-4ac)}/2a
= [2±√{4-4×1×5}/2
= (2±√-16)/2
= (2±4i)/2 = 1 ± 2i
Que-5: 3x² – 17x + 25 = 0
Sol: Given quadratic equation be,
3x² – 17x + 25 = 0
On comparing with ax² + bx + c = 0 ; we have
a = 3 ; b = – 17 ; c = 25
Then by quadratic formula, we have
∴ x = {−b±√(b²-4ac)}/2a
∴ x = [−(−17)±√{(−17)²−4×3×25}/(2×3)
= {17±√(289−300)}/6
⇒ x = {17±√-11}/6
= {17±√11i}/6
Que-6: x² + 3x – 3 = 0, giving your answer correct to two decimal places.
Sol: Given quadratic eqn. be, x² + 3x – 3 = 0
On comparing with ax² + bx + c = 0 ; we have
a = 1 ; b = 3 ; c = – 3
Then by using quadratic formula,
∴ x = {−b±√(b²-4ac)}/2a
= [−3±√{3²−4×1×(−3)}]/(2×1)
= (−3±√21)/2 = (−3±4.5826)/2
= 0.7913 – 3.7913
⇒ x = 0.79 – 3.79 (correct to two decimal places)
Que-7: 5x² – x + 4 = 0
Sol: Given quadratic eqn. be 5x² – x + 4 = 0
On comparing with ax² + bx + c = 0 ; we have
a = 5; b = – 1; c = 4
Then by quadratic formula, we have
x = {−b±√(b²-4ac)}/2a
= [−(−1)±√{(−1)²−4×5×4}]/(2×5)
⇒ x = (1±√-79)/10
= (1±√79i)/10
Que-8: √3x² – √2x + 3√3 = 0
Sol: Given quadratic eqn. be,
√3x² – √2x + 3√3 = 0
On comparing with ax² + bx + c = 0, we have
a = √3 ; b = – √2 ; c = 3√3
Then by quadratic formula, we have
x = {−b±√(b²-4ac)}/2a
= [√2±√{(−√2)2−4×√3×3√3}/(2×√3)
x = {√2±√(2-36)}/2√3
= {√2±√34i}/2√3
Que-8: (x²+8)/11 = 5x – x² – 5
Sol: Given quadratic eqn. can be written as
x² + 8 = 11 (5x – x² – 5)
⇒ 12x² + 55x + 63 = 0
On comparing with ax² + bx + c = 0 ; we
have
a = 12; b = – 55 ; c = 63
By quadratic formula, we have
x = {−b±√(b²-4ac)}/2a
= [55±√{(−55)²−4×12×63}/(2×12)
= {55±1}/24
= 56/24, 54/24 i.e. 7/3, 9/4
Que-10: {2x/(x−4)} + {(2x−5)/(x−3)} = 8*(1/3)
Sol: Given quadratic equation be,
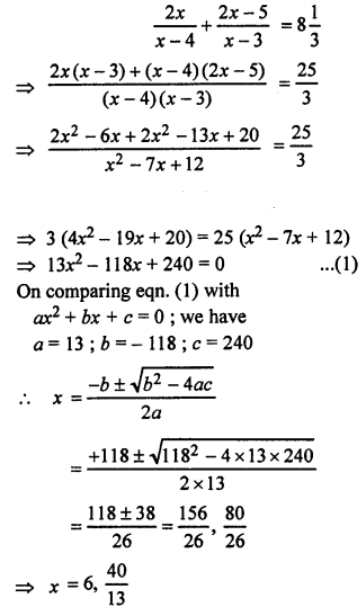
Que-11: The number of real solutions of the equation x² – 3|x| + 2 = o is
(a) 3
(b) 4
(c) 1
(d) 3
Sol: Given eqn. be x² – 3|x| + 2 = o = 0
⇒ |x|² – 3|x| + 2 = 0 [∵ |x|² = x²]
⇒ (|x| – 1)(|x| – 2) = 0
either | x | – 1 = 0 or | x | – 2 = 0
⇒ | x | = 1 or |x| = 2
⇒ x = ± 1 or x = ± 2
∴ x = ± 1, ± 2
–: End of Quadratic Equations Class 11 OP Malhotra Exe-10A ISC Math Ch-10 Solution :–
Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions
Thanks
Please share with your friends