Quadratic Equations Class 11 OP Malhotra Exe-10D ISC Maths Solutions Ch-10 Solutions. In this article you would learn about Special roots, signs of the roots and common roots. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Quadratic Equations Class 11 OP Malhotra Exe-10D ISC Maths Solutions Ch-10
| Board | ISC |
| Publications | S Chand |
| Subject | Maths |
| Class | 11th |
| Chapter-10 | Quadratic equations |
| Writer | O.P. Malhotra |
| Exe-10(D) | Special roots, signs of the roots and common roots. |
Exercise- 10D
Quadratic Equations Class 11 OP Malhotra Exe-10D Solution.
Que-1: Find the condition that one root of ax² + bx + c = 0 may be
(i) three times the other, (ii) it times the other, (iii) more than the other by h.
Sol: (i) Let the roots of given eqn. be ax² + bx + c = 0 are α and 3α.
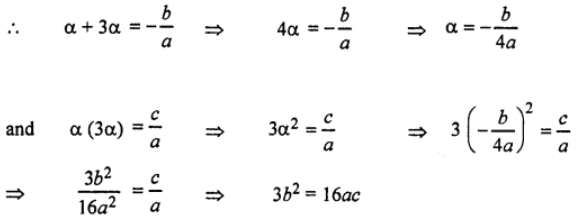
which gives the required condition.
(ii) Let the roots of given eqn. are α and nα
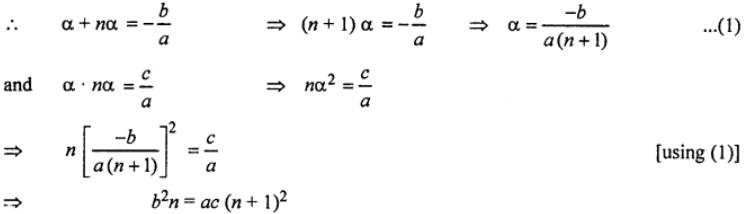
which gives the required condition.
(iii) Let the roots of given eqn. ax² + bx + c = 0 are α and α + h.

which gives the required condition.
Que-2: Find the condition that the ratio between the roots of the equation ax² + bx + c = 0 may be m : n.
Sol: Given quadratic eqn.be ax² + bx + c = 0 …(1)
Let the roots of eqn. (1) are mα and nα.
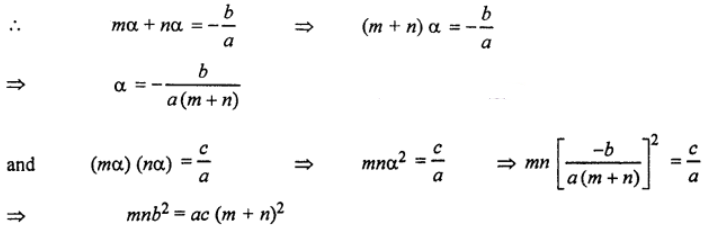
which gives the required condition.
Que-3: If the ratio of the roots of the equation x² + px + q = 0 is equal to the ratio of the roots of x² + lx + m = 0, prove that mp² = ql².
Sol: Let α and ß are the roots of eqn. x² + px + q = 0
∴ α + ß = – p ; αß = q
and γ, δ are the roots of the eqn.
x² + lx + m = 0
γ + δ = – l and γδ = m
according to given condition, we have
α/ß = γ/δ
Applying Componendo and Dividendo ; we have,
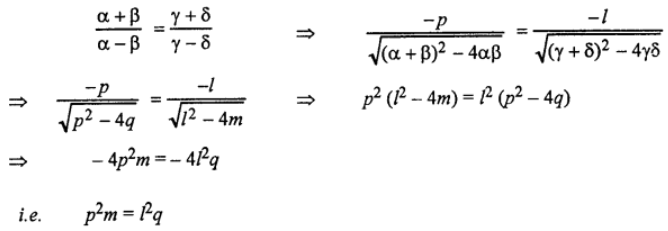
which is the required condition.
Que-4: For what values of a and b, the equation x² + (2a – 3) x = 3b + 4 should have both the roots zero ?
Sol: Given quadratic eqn. be, x² + (2a – 3) x – (3b + 4) = 0 …(1)
Now both the roots of eqn. (1) are zero.
∴ coeff. of x = 0 and constant term = 0
⇒ 2a – 3 = 0 and 3b + 4 = 0 ⇒ a = 3/2 and b = -4/3
Que-5: Find the values of X and p if both the roots of the equation (3λ + 1)x² = (2λ + 3λ) x – 3 are infinite.
Sol: We know that if a and p are the roots of eqn. ax² + bx + c = 0.
Then (1/α) and (1/ß) are the roots of eqn. cx² + bx + a = 0
Hence both roots of ax² + bx + c = 0 are infinite if roots of cx² + bx + a = 0 are zero.
∴ a = 0 and b = 0
Thus both the roots of eqn. (3λ + 1) x² – (2λ + 3μ) x + 3 = 0 are infinite.
if coeff. of x² = 0 and coeff. of x = 0
if 3λ + 1 = 0 and 2λ + 3μ = 0
if λ = – 13 and – 23 + 3μ = 0 ⇒ μ = (2/9)
Thus λ = – (1/3) and μ = (2/9)
Que-6: Find m so that the roots of the equation (x²−bx)/(ax−c) = (m−1)/(m+1) may be equal in magnitude and opposite in sign.
Sol: The given quadratic equation be
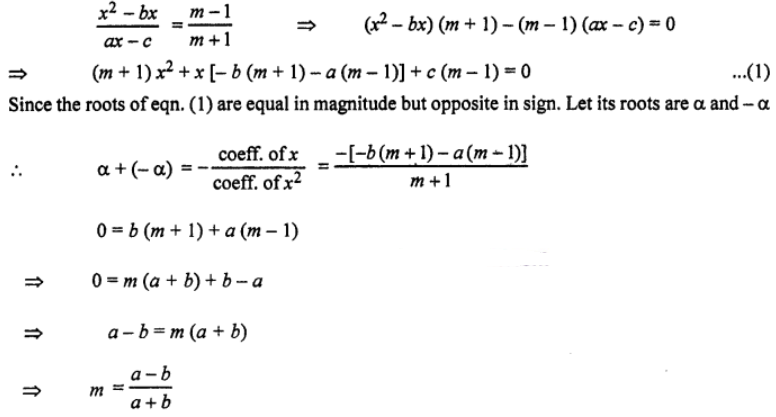
Que-7: (i) The roots of the quadratic equation 4x² – (5a + 1) x + 5a = 0, are p and q. If q = 1 + p, calculate the possible values of a, p and q.
(ii) Find the values of p for which the quadratic equation x² – px + p + 3 = 0 has
(a) coincident roots, (b) real distinct roots, (c) one positive and one negative root.
Sol: (i) Given the roots of eqn. 4x² – (5a + 1) x + 5a = 0 are p and q.
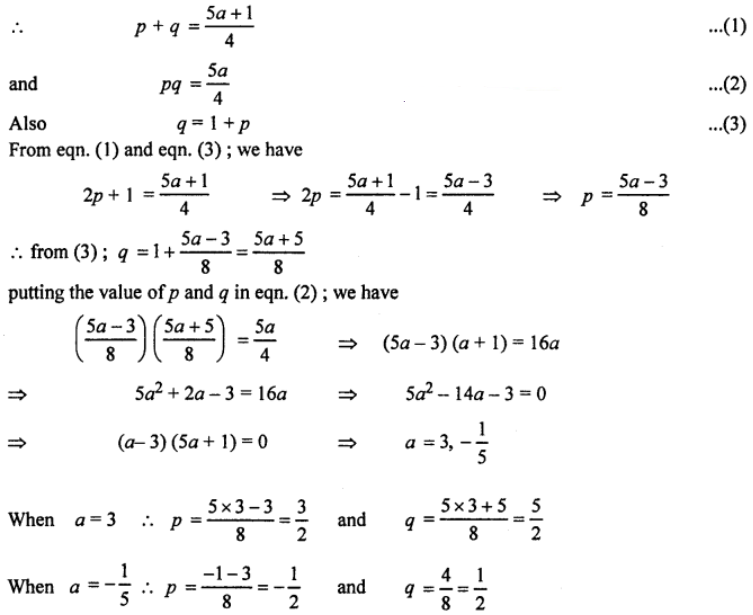
(ii) Given quadratic eqn. be, x² – px + p + 3 = 0 …(1)
On comparing eqn. (1) with ax² + bx + c = 0
We have, a = 1 ; b = – p ; c = p + 3
(a) Roots of eqn. (1) are coincident roots
∴ discriminant = 0
⇒ b² – 4 ac = 0
⇒ (- p)² – 4 x 1 x (p + 3) = 0
⇒ p² – 4p – 12 > 0
⇒ (p + 2) (p – 6) = 0
⇒ p = – 2, 6
(b) roots of eqn. (1) are real and distinct.
∴ D > 0
⇒ b² – 4ac > 0
⇒ p² – 4p – 12 > 0
⇒ (p + 2) (p – 6) > 0
⇒ p < – 2 or p > 6
(c) given one root of eqn. (1) be positive and other be negative i.e. roots of eqn. (1) are of opposite sign.
∴ product of roots < 0
c/a < 0
∴ c and a are of opposite sign
Here a = 1 > 0
∴ c < 0 ⇒ p + 3 < 0 ⇒ p < – 3
Que-8: Find the values of m for which the quadratic equation x² – m (2x – 8) – 15 = 0 has
(i) equal roots, (ii) both roots positive.
Sol: The given quadratic eqn. be x² – m (2x – 8) – 15 = 0
⇒ x² – 2mx + 8m – 15 = 0 …(1)
On comparing eqn. (1) with ax² + bx + c = 0 ; we have,
a = 1 ; b = – 2m and c = 8m – 15
(i) Roots of eqn. (1) are equal.
∴ discriminant = 0 ⇒ b² – 4ac = 0 (- 2m)² – 4 x 1 x (8m – 15) = 0
⇒ 4m² – 32m + 60 = 0
⇒ m² – 8m + 15 = 0
⇒ (m – 3) (m – 5) = 0
⇒ m = 3, 5
(ii) both roots of eqn. (1) are positive
∴ Sum of roots > 0 ⇒ – b/a > 0 ⇒ b/a < 0
i.e. b and a are opposite sign.
Here a = 1 > 0
∴ b < 0 ⇒ – 2m < 0 ⇒ m > 0
and product of roots > 0 ⇒ c/a > 0
∴ c and a are of same sign.
Here a = 1 > 0 ∴ c > 0
⇒ 8m – 15 > 0
⇒ m > 15/8
Therefore m > 0 and m > 15/8.
Que-9: If a + b + c = 0, prove that the roots of ax² + bx + c = 0 are rational. Hence, show that the roots of (p + q) x² – 2px + (p – q) = 0 are rational.
Sol: Given quadratic equation be ax² + bx + c = 0 …(1)
Clearly x = 1 satisfy eqn. (1)
∵ a + b + c = 0 (given)
Thus x = 1 be the roots of eqn. (1).
Since irrational or imaginary/non-real roots occurs in conjugate pair. Other root of eqn. (1) must be rational.
Hence the general condition for the roots of eqn. (1) are rational be a + b + c = 0
Also, the given quadratic eqn. be, (p + q) x² – 2px + p – q = 0 …(2)
Here a + b + c = p + q – 2p + p – q = 0
∴ roots of eqn. (2) are also rational.
Que-10: Show that the roots of (x – b) (x – c) + (x – c) (x – a) + (x – a) (x – b) = 0 are real, and that they cannot be equal unless a = b = c.
Sol: Given quadratic eqn. be (x – b) (x – c) + (x – c) (x – a) + (x – a) (x – b) = 0
⇒ 3x² – 2 (a + b + c) x + be + ca + ab = 0 …(1)
On comparing with Ax² + Bx + C = 0
We have, A = 3; B = – 2 (a + b + c) and c = ab + bc + ca
Now roots of eqn. (1) are real if D ≥ 0
Here D = b² – 4AC = [- 2 (a + b + c)]² – 4 x 3 (ab + bc + ca)
= 4 [(a + b + c)² – 3 (ab + bc + ca)]
= 4 [a² + b² + c² – ab – bc – ca]
= 2 [2a² + 2b² + 2c² – 2ab – 2bc – 2ca]
= 2 [(a – b)² + (b – c)² + (c – a)²] > 0 [∵ (a – b)² > 0 ; (b – c)² > 0 and (c – a)² > 0]
Hence the roots of given eqn. (1) are real.
Now the roots of given eqn. are equal
if Discriminant = 0 if (a – b)² + (b – c)² + (c – a)² = 0
i.e. if a – b = 0 and b – c = 0 and c – a = 0 i.e. if a = b = c
Hence the roots of eqn. (1) cannot be equal unless a = b = c
Que-11: Determine the values of m for which the equations 3x² + 4mx + 2 = 0 and 2x² + 3x – 2 = 0 may have a common root.
Sol: Let α be the common root of both given quadratic equations
3x² + 4mx + 2 = 0 and
2x² + 3x – 2 = 0
i.e. 3α² + 4mα + 2 = 0
2α² + 3α – 2 = 0
By cross multiplication method, we have

Que-12: Find the value of k, so that the equation 2x² + kx – 5 = 0 and x² – 3x – 4 = 0 may have one root common.
Sol: Let a be the common root of both given equations
2x² + kx – 5 = 0 and x² – 3x – 4 = 0
∴ 2a² + kα – 5 = 0 …(1)
α² – 3α – 4 = 0 …(2)
By cross multiplication method, we have

Que-13: If ax² + bx + c = 0 and bx² + cx + a = 0 have a common root, prove that a + b + c = 0 or a = b = c.
Sol: Let a be the common root of both equations ax² + bx + c = 0 and bx² + cx + a = 0
i.e. aα² + bα + c = 0 …(1)
bα² + cα + a = 0 …(2)
By cross multiplication method, we have

Que-14: The equations x² + x + a = 0 and x² + ax + 1 = 0 have a common real root
(a) for no value of a
(b) for exactly one value of a
(c) for exactly two values of a
(d) for exactly three values of a
Sol: Let α be the common real root of equations
x² + x + a = 0 and x² + ax + 1 = 0
∴ α² + α + a = 0 …(1)
and α² + aα + 1 = 0 …(2)
eqn. (1) – eqn. (2) gives ;
(1 – a)α + a – 1 = 0 ⇒ α = 1
∴ from (1); 1 + 1 + a = 0 ⇒ a = – 2
–: End of Quadratic Equations Class 11 OP Malhotra Exe-10D ISC Maths Ch-10 Solutions. :–
Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions
Thanks
Please share with your friends


