Quadratic Equations Class 11 OP Malhotra Exe-10E ISC Maths Solutions

Quadratic Equations Class 11 OP Malhotra Exe-10E ISC Maths Solutions Ch-10 Solutions. In this article you would learn about Graph of the Quadratic Equations. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Quadratic Equations Class 11 OP Malhotra Exe-10E ISC Maths Solutions Ch-10

Board	ISC
Publications	S Chand
Subject	Maths
Class	11th
Chapter-10	Quadratic equations
Writer	O.P. Malhotra
Exe-10(E)	Graph of the Quadratic Equations.

Exercise- 10E

Quadratic Equations Class 11 OP Malhotra Exe-10E Solution.

Draw the graph of each of the following quadratic functions.

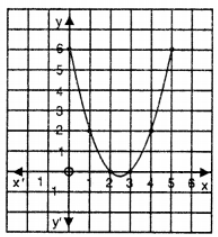
Que-1: y = x² – 5x + 6 ; 0 ≤ x ≤ 5.

Sol: Given y = x² – 5x + 6 ; 0 ≤ x ≤ 5
The table of values is given as under :

Que-2: y = – x² + 2x + 3 ; – 3 ≤ x ≤ 5.

Sol: Given y = – x² + 2x + 3 where – 3 ≤ x ≤ 5
The table of values is given as under;

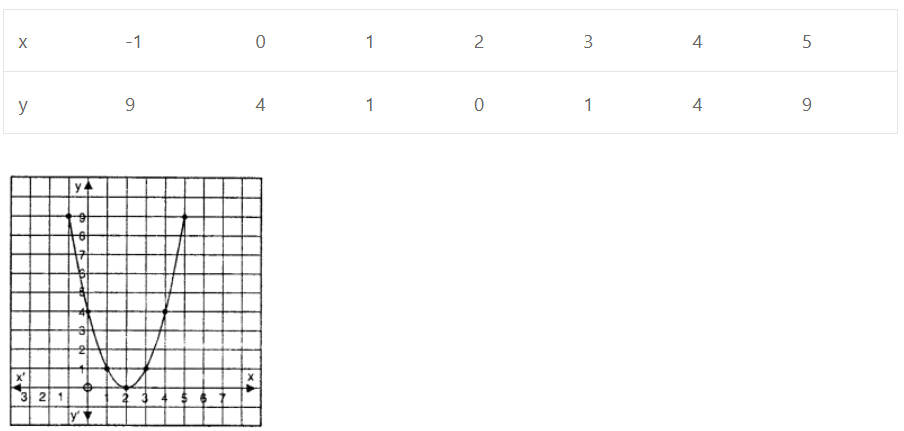
Que-3: y = x² – 4x + 4 ; – 1 ≤ x ≤ 5.

Sol: Given y = x² – 4x + 4 ; – 1 ≤ x ≤ 5
The table of values is given as under

Que-4: Solve graphically and compare your answer with algebraic solution either by factorization or formula method :
(i) y = x² – 5x + 6
(ii) y = – x² + 2x + 3
(iii) y = x² – 4x + 4
(iv) y = x² – x – 6
(v) y = x² – 6x + 9
(vii) y = x² – 4x + 5 = 0
(viii) y = x² + 2x + 2 = 0

Sol: (i) y = x² – 5x + 6
The table of values is given as under:

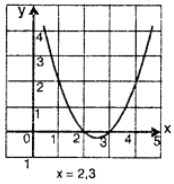
Clearly the graph of curve intersects x-axis at two points at
x = 2 and x = 3
∴ x = 2, 3

Verification : y = x² – 2x – 3x + 6 = x (x – 2) – 3 (x – 3)
⇒ y = (x – 2) (x – 3)
Clearly x = 2 and x = 3 are the two solutions of given curve.

(ii) Given y = – x² + 2x + 3
The table of values is given as under :

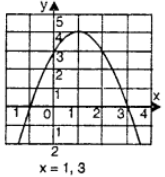
Clearly the graph of curve intersects x-axis at two points at x = – 1 and x = 3
Verification : y = – x³ + 2x + 3 = – x² + 3x – x + 3
= – x (x – 3) – 1(x – 3)
= – (x – 3) (x + 1)
Clearly x = – 1 and x = 3 are two solutions of given curve.

(iii) Given y = x² – 4x + 4
The table of values is given as under :

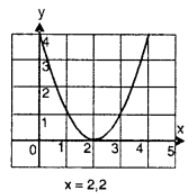
Clearly the graph of curve intersects x-axis at one point i.e. x = 2
Verification : y = x² – 4x + 4 = (x – 2)²
Clearly x = 2 be the solution of given curve.

(iv) Given y = x² – x – 6
The table of values is given as under

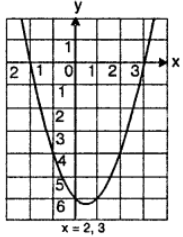
Clearly the graph meets x-axis at (- 2, 0) and (3, 0).
∴ x = – 2, 3 are the real solutions of given curve

Verification : y = x² – x – 6 = x² – 3x + 2x – 6
= x (x – 3) + 2 (x – 3) = (x + 2) (x – 3)
Clearly – 2 and 3 are the solutions of y = x² – x – 6 = 0

(v) Given eqn. of curve be y = x² – 6x + 9
The tale of values is given as under :

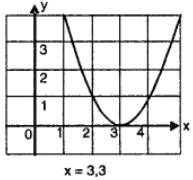
Clearly the graph of curve intersects x-axis at (3, 0).
∴ x = 3, 3 be the solution of given curve.

Verification : y = x² – 6x + 9 = x² – 3x – 3x + 9
= x (x – 3) – 3 (x – 3) = (x – 3)²
Clearly x = 3 be the solution of given curve.

(vi) Given eqn. of curve bey = – x² + x + 12 ⇒ y = – (x² + x – 12)
The table of values is given as under :

Clearly the graph of the curve intersects x-axis at x = – 4 and x = 3.
Hence x = – 4, 3 are two real solutions of given curve.

Verification : y = – (x² – 4x + 3x – 12) = – [x (x – 4) + 3 (x – 4)]
= – (x + 3)(x – 4)
Clearly x = – 3 and 4 are the solutions of y = – x² + x + 12 = 0

(vii) Given curve be y = x² – 4x + 5 = 0
The table of values is given as under

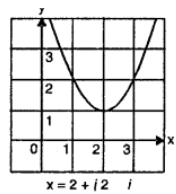
Clearly the curve does not meets x-axis at any point so it has no real solution.
Verification : x² – 4x + 5 = 0 ⇒ x = [4±√{16−4×1×5}]/2
= (4±2i)/2 = 2±i

(viii) Given curve be y = x² + 2x + 2 = 0
The table of values is given as under :

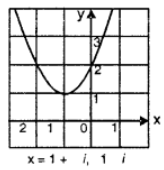
Clearly the graph of curve does not meet x-axis
∴ given curve has no real solution.
Verification : y = x² + 2x + 2 = 0
⇒ x = {−2±√(4-8)}/2
⇒ x = (−2±2i)/2
⇒ x = – 1 ± i