Quadratic Equations OP Malhotra S.Chand Class-10 ICSE Maths Ch-5

Quadratic Equations OP Malhotra S.Chand Class-10 ICSE Maths Solutions Ch-5.  We Provide Step by Step Answer of Exe-5 Quadratic Equations with Self Evaluation and Revision of S Chand OP Malhotra Maths . Visit official Website CISCE  for detail information about ICSE Board Class-10.

Quadratic Equations OP Malhotra S.Chand Class-10 ICSE Maths Solutions Ch-5

---

-: Select Topics :-

 video concept

Exe-5.1,

Exe-5.2,

Exe-5.3,

Exe-5.4,

Exe-5.5,

---

Quadratic Equations OP Malhotra S.Chand Class-10 ICSE Maths Solutions Ch-5

Quadratic Equation

When we equate a quadratic polynomial to a constant, we get a quadratic equation.

Any equation of the form p(x)=c, where p(x) is a polynomial of degree 2 and c is a constant, is a quadratic equation.

The standard form of a Quadratic Equation

The standard form of a quadratic equation is $a{x}^2+bx+c=0$, where a,b and c are real numbers and $a\ne 0$.
‘a’ is the coefficient of $x^2$. It is called the quadratic coefficient. ‘b’ is the coefficient of x. It is called the linear coefficient. ‘c’ is the constant term.

Solving QE by Factorisation

Roots of a Quadratic equation

The values of $x$ for which a quadratic equation is satisfied are called the roots of the quadratic equation.

If α is a root of the quadratic equation $a{x}^2+bx+c=0$, then$a{\alpha }^2+b\alpha +c=0.$

A quadratic equation can have two distinct real roots, two equal roots or real roots may not exist.

Graphically, the roots of a quadratic equation are the points where the graph of the quadratic polynomial cuts the x-axis.

Consider the graph of a quadratic equation $x^2-4=\mathrm{0:}$

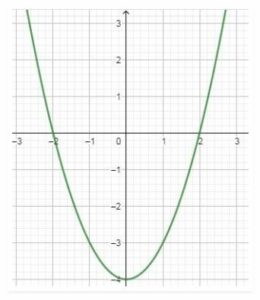
In the above figure, -2 and 2 are the roots of the quadratic equation $x^2-4=0$
Note:

• If the graph of the quadratic polynomial cuts the x-axis at two distinct points, then it has real and distinct roots.
• If the graph of the quadratic polynomial touches the x-axis, then it has real and equal roots.
• If the graph of the quadratic polynomial does not cut or touch the x-axis then it does not have any real roots.

Discriminant

For a quadratic equation of the form $a{\mathrm{x²}}^{}+bx+c=0,$ the expression ${\mathrm{b²}}^{}-4ac$ is called the discriminant, (denoted by D), of the quadratic equation.
The discriminant determines the nature of roots of the quadratic equation based on the coefficients of the quadratic equation.

Formation of a quadratic equation from its roots

To find out the standard form of a quadratic equation when the roots are given:
Let $\alpha$ and $\beta$ be the roots of the quadratic equation $a{\mathrm{x²}}^{}+bx+c=0$. Then,
$(x-\alpha )(x-\beta )=0$
On expanding, we get,
${\mathrm{x²}}^{}-(\alpha +\beta )x+\alpha \beta =0,$ which is the standard form of the quadratic equation. Here, $a=1,b=-(\alpha +\beta )andc=\alpha \beta .$

Sum and Product of Roots of a Quadratic equation

Let $\alpha and\beta$ be the roots of the quadratic equation $a{\mathrm{x²}}^{}+bx+c=0.$ Then,
Sum of roots $=\alpha +\beta$=-b/a
Product of roots $=\alpha \beta$= c/a

---

Exe-5.1,

Quadratic Equations OP Malhotra S.Chand Class-10 ICSE Maths Solutions Ch-5

Solve :

Question 1:

(i) (x – 3) (x + 7) = 0

(ii) (3x + 4) (2x – 11) = 0

Question 2:

x² = 4x

Question 3:

…………………….

……………………..

……………………..

Question 23:

√2 x² – 3x – 2 √2 = 0

Question 24:

a(x² + 1) – x (a² + 1) = 0

---

Exe-5.2,

 OP Malhotra S.Chand Class-10 ICSE Maths Solutions Ch-5

Solve of the following equations by reducing them to quadratic equations :

Question 1:

x⁴ + 5x² -36 = 0

Question 2:

x⁴ – 25x² + 144 = 0

Question 3:

………………………

………………………

………………………..

Question 13:

√4x ………………

---

Exe-5.3,

Quadratic Equations OP Malhotra S.Chand Class-10 ICSE Maths Solutions Ch-5

Using quadratic formula, find the roots of the following equations :

Question 1:

2x² + x – 3 = 0

Question 2:

6x² + 7x – 20 = 0

Question 3:

…………………………

…………………………..

…………………………

……………………………

Question 21:

Solve using the quadratic formula :

(i)……..

(ii)…………

(iii)………….

---

Exe-5.4,

Quadratic Equations OP Malhotra Class-10 ICSE Maths Solutions Ch-5

Question 1:

Using the discriminant to determine the ………………… quadratic equations :

(i)……..

(ii)…………

(iii)………….

(iv)…………

Question 2:

Without finding the roots ……………………. equations .

………………..

………………..

Question 3:

……………………

…………………….

………………………

Question 8:

If the root of the equations …………………………. 2b = a + c.

---

Exe-5.5,

Quadratic Equations S.Chand Class-10 ICSE Maths Solutions Ch-5

Question 1:

The sum of the squares of two consecutive positive even integers is 100 find the integers .

Question 2:

Find two ……………………. is 117.

Question 3:

………………….

……………………..

…………………..

Question 27:

A man purchased …………………….. horses did he buy ?

Question 28:

A trader bought a number of article for 1200. Ten were damaged and he sold each of the rest at 2 more than what he paid for it, thus getting a profit of 60 on the whole transaction. Taking the number of article he bought as x, from an equation in x and solve.

— : End of Quadratic Equations OP Malhotra S Chand Solutions :–

---

Return to :-   OP Malhotra S Chand Solutions for ICSE Class-10 Maths

Thanks

Please Share with Your Friends