Rational and Irrational Numbers Class 9 RS Aggarwal Exe-1B Goyal Brothers ICSE Foundation Maths Solutions. In this article you will learn how to insert number between two ratinal number. Visit official Website CISCE for detail information about ICSE Board Class-9 Mathematics.

Rational and Irrational Numbers Class 9 RS Aggarwal Exe-1B Goyal Brothers ICSE Foundation Maths Solutions
| Board | ICSE |
| Publications | Goyal brothers Prakshan |
| Subject | Maths |
| Class | 9th |
| Chapter-1 | Rational and Irrational Numbers |
| Writer | RS Aggrawal |
| Book Name | Foundation |
| Topics | Solution of Exe-1B |
| Academic Session | 2024-2025 |
How to Insert number between two ratinal number easily
To get the rational numbers between two rational numbers with different denominators, equlise the denominators by finding their LCM or by multiplying the denominators of one to both the numerator and denominator of the other. Then multiply both ratinal number in numerator and denominator seperately by (n+1) number where n is number to insert between them
Page- 10
Exercise- 1B
Rational and Irrational Numbers Class 9 RS Aggarwal Exe-1B Goyal Brothers ICSE Foundation Maths Solutions.
Que-1: Write the additive inverse of :
(i) 5 (ii) -7 (iii) 5/9 (iv) -3/17 (v) 0 (vi) 11*(5/17) (vii) -5*(3/8) (viii) -37 (ix) 1
Solution- The additive inverse of any given number can be found by changing the sign of it
(i) -5
(ii) 7
(iii) -5/9
(iv) 3/17
(v) 0
(vi) -192/17
(vii) 43/8
(viii) 37
(ix) -1
Que-2: Write the multiplicative inverse of :
(i) 9 (ii) -1 (iii) 11/16 (iv) 5*(1/4) (v) -2/3 (vi) 17*(3/20) (vii) -18*(1/2) (viii) -5 (ix) -20/41
Solution- when the product of two numbers is 1, they are said to be multiplicative inverses of each other
(i) 1/9
(ii) -1
(iii) 16/11
(iv) 21/4 = 4/21
(v) -3/2
(vi) 343/20 = 20/343
(vii) -37/2
(viii) -1/5
(ix) -41/20
Que-3: Represent each of the following on the number line :
(i) 3/7 (ii) 16/5 (iii) -4/9 (iv) -18/11 (v) -3*(1/6)
Solution- (i) 3/7
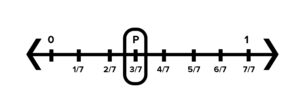
(ii)
Que-4: Find a rational number between 3/5 and 7/9
Solution- Consider 3/5 and 7/9
LCM of 5 and 9 = 45
So, making the denominators of both 3/5 and 7/9 equal to 45:
3/5 × 9/9 = 27/45 and 7/9 × 5/5 = 35/45
Thus, 28/45, 29/45, 30/45 are rational numbers between the given numbers.
Que-5: Find two rational number between :
(i) 2 and 3 (ii) 1/3 and 2/5 (iii) 3/4 and 1*(1/5) (iv) -2 and 1
Solution- (i) Rational numbers are the numbers which can be represented in pq form where, q ≠ 0.
Given natural numbers, 2 and 3
Let the two rational numbers between 2 and 3 be a and b.
Use average method to find a and b.
Average method suggests adding the two given rational numbers and then dividing the sum by two.
So,
a = 1/2 (2+3)
a = 5/2
b = 1/2 (2+a)
b = [(2+5/2)]/2
b = 9/4
Hence, the two rational numbers between 2 and 3 are 5/2 and 9/4.
(ii) We start by making the denominators the same,
We get:
1/3 × 5/5 = 5/15
4/5 × 3/3 = 12/15
therefore rational numbers are
6/15, 7/15, 8/15
(iii) 3/4 and 6/5
Convert the fractions to have a common denominator of 20:
3/4 = (3×5)/(4×5) = 15/20
6/5 = (6×4)/(5×4) = 24/20
We now need to find three rational numbers between 15/20 and 24/20. We can choose any fractions that fall between these two values. Here are three examples:
16/20 = 45/20
17/20
18/20 = 9/10
(iv) −2 = −20/10
1 = 10/10
We want to find three rational numbers between −20/10 and 10/10.
A number slightly greater than −20/10 could be −15/10 = −1.5
Another number could be −10/10 = −10/10 = −1
Another could be −5/10 = −0.5
Here are three rational numbers between -2 and 1: −1.5, −1, −0.5
Que-6: Find three rational number between :
(i) 4 and 5 (ii) 1/2 and 3/5 (iii) -1 and 1 (iv) 2*(1/3) and 3*(2/3) (v) -1/2 and 1/3 (vi) -1/3 and 1/4
Solution- (i) Given natural numbers, 4 and 5
Let the three rational numbers between 4 and 5 be 𝑎,𝑏,𝑐
So,
⇒ 𝑎 = 1/2(4+5)
𝑎 = 9/2
⇒ 𝑏 = 1/2(4+𝑎)𝑏
= 1/2(4+92)𝑏
= 1/2(8+92) = 17/4
⇒ 𝑐 = 1/2(𝑎+5)𝑐
= 1/2(92+5)𝑐
= 1/2(9+102) =19/4
Therefore, the three rational numbers between 4 and 5 are 9/2, 17/4, 19/4.
(ii) Get a common denominator (simplest: 10).
then 1/2 = 5/10 and 3/5 = 6/10.
Now you make more space to identify rationals in between:
since you want 3 in between I suggest to extend the fraction to a denominator of 40:
1/2 = 20/40, 3/5=24/40
then the rational numbers you are looking for are 21/40, 22/40, 23/40
(iii) You can select any fractions or decimals that fall within this interval. Here are three examples:
−1/2, 0, 1/2
Each of these numbers is rational and lies between -1 and 1.
(iv) Let’s first express the given fractions as decimals:
7/3 = 2.3333…(repeating as 2.333‾)
11/3 = 3.6666…(repeating as 3.666‾)
Here are three such rational numbers:
8/3 = 2.6666…(repeating as 2.666‾)
9/3 = 3
10/3 = 3.3333…(repeating as 3.333‾)
These three rational numbers are clearly between 7337 and 113311:
7/3 < 8/3 < 11/3
7/3 < 9/3 < 11/3
7/3 < 10/3 < 11/3
Therefore, the three rational numbers between 7337 and 113311 are:
8/3, 9/3, and 10/3.
(v) Average of −1/2 and 1/3:
Average = [−1/2+13/2] = [−3/6+2/6]/2 = (−1/6)/2 = −1/12
Adding a small positive rational number, say 1/24, to −1/12, we get:
−1/12+1/24 = [−2/24+1/24] = −1/24
Subtracting a small positive rational number, say 1/24, from −1/12, we get:
−1/12−1/24 = −2/24−1/24 = −3/24 = −1/8
So, three rational numbers between −1/2 and 1/3 are −1/24, −1/12, and −1/8.
(vi) Average of -1/3 and 1/4 is (-1/3 + 1/4) / 2 = (-4/12 + 3/12) / 2 = (-1/12) / 2 = -1/24. Adjusting slightly, we get -1/24 – 1/6 = -5/24.
Average of -1/3 and 1/4 is (-1/3 + 1/4) / 2 = (-4/12 + 3/12) / 2 = (-1/12) / 2 = -1/24. Adjusting slightly, we get -1/24 + 1/12 = -1/24 + 2/24 = 1/24.
Average of -1/3 and 1/4 is (-1/3 + 1/4) / 2 = (-4/12 + 3/12) / 2 = (-1/12) / 2 = -1/24. Adjusting slightly, we get -1/24 + 1/6 = 5/24.
So, three rational numbers between -1/3 and 1/4 are -5/24, -1/24, and 5/24.
Que-7: Find four rational numbers between 4 and 4.5
Solution- let’s express 4 and 4.5 as fractions:
4 = 4.0 = 40/10
4.5 = 45/10
Now we need to find fractions between 400/100 and 450/100:
A number slightly greater than 400/100 could be 410/100 which is 4.1.
Another number could be 420/100 which is 4.2.
and Another could be 430/100 which is 4.3.
Another could be 440/100 which is 4.4.
Thus, we have found four rational numbers:
410/100 = 4.1
420/100 = 4.2
430/100 = 4.3
440/100 = 4.4
These numbers are all between 4 and 4.5 and are rational. Therefore, four rational numbers between 4 and 4.5 are: 4.1, 4.2, 4.3, 4.4
Que-8: Find six rational number between 3 and 4.
Solution- First, let’s express 3 and 4 in terms of fractions with a common denominator to facilitate finding numbers in between:
3 = 30/10
4 = 40/10
We want to find six rational numbers between 30/10 and 40/10.
Let’s use 100 as the common denominator:
3 = 300/100
4 = 400/100
Now we need to find six fractions between 300/100 and 400/100:
A number slightly greater than 300/100 could be 310/100 = 3.1
Another number could be 320/100 = 3.2
Another could be 330/100 = 3.3
and Another could be 340/100 = 3.4
Another could be 350/100 = 3.5
Another could be 360/100 = 3.6
These numbers are all between 3 and 4 and are rational. Therefore, six rational numbers between 3 and 4 are: 3.1, 3.2, 3.3, 3.4, 3.5, 3.6
: End of Rational and Irrational Numbers Class 9 RS Aggarwal Exe-1B Goyal Brothers ICSE Foundation Maths : —
Return to :- RS Aggarwal Solutions for ICSE Class-9 Mathematics (Goyal Brother Prakashan)
Thanks
Please Share with your friends if helpful


