Relations and Functions Class 11 OP Malhotra Exe-2A ISC Maths Solutions Ch-2 Solutions. In this article you would learn about Cartesian product and Ordered Triplet. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Relations and Functions Class 11 OP Malhotra Exe-2A ISC Maths Solutions Ch-2

Board	ISC
Publications	S Chand
Subject	Maths
Class	11th
Chapter-2	Relations and Functions
Writer	OP Malhotra
Exe-2(A)	Cartesian product and Ordered Triplet.

Exercise- 2A

Relations and Functions Class 11 OP Malhotra Exe-2A Solution.

Que-1: x ∈ {2, 4,6,9} and y ∈ {4, 6, 18, 27, 54}. From all ordered pairs (x, y) such that x is a factor of y and x < y.

Sol: x ∈ {2, 4, 6, 9} and y ∈ {4, 6, 18, 27, 54}
we want to find all ordered pairs (x, y) such that x is a factor of y and x < y
Now 2 be a factor of 4, 6, 18, 54 and 2 < 4, 2 < 6, 2 < 18 and 2 < 54
∴ possible ordered pairs are ; (2, 4), (2, 6), (2, 18), (2, 54)
Now 4 is a factor of 4 but 4 ≮  4
Now 6 is a factor of 18 and 54 and 6 < 18, 6 < 54
Then possible ordered pairs in this case are (6, 18) and (6, 54).
9 is a factor of 18, 27, 54, s.t 9 < 18 ; 9 < 27 and 9 < 54.
Then possible ordered pairs in this case are :
(9, 18), (9, 27) and (9, 54).
Hence required possible ordered pairs are :
{(2, 4), (2, 6), (2, 18), (2, 54), (6, 18), (6, 54), (9, 18), (9, 27), (9, 54)}

Que-2: Find the numbers x and y if (x-2, y+5) = [-2, (1/3)]

Sol:  (x-2, y+5) = (-2, (1/3))
x-2 = -2
x = 0
y+5 = 1/3
y = -14/3

Que-3: If A = {1, 3, 5, 7} and B = {2, 4, 6}, find
(i) A x A
(ii) A x B
(iii) B x A
(iv) B x B
(v) n (A x A)
(vi) n (A x B)
(vii) n (B x A)
(viii) n (B x B)

Sol: Given A = {1, 3, 5, 7} and B = {2, 4, 6}

(i) ∴ A x A = {1,3,5, 7} x {1,3, 5,7}
= {(1, 1), (1, 3), (1, 5), (1, 7), (3, 1), (3, 3), (3, 5), (3, 7), (5, 1), (5, 3), (5, 5), (5, 7), (7, 1), (7, 3), (7, 5), (7, 7)} [∵ A x B = {(x, y); x ∈ A and y ∈ B}]

(ii) A x B = {1, 3, 5, 7} x {2, 4, 6}
= {(1, 2), (1, 4), (1, 6), (3, 2), (3, 4), (3, 6), (5, 2), (5, 4), (5, 6), (7, 2), (7, 4), (7, 6)}

(iii) B x A = {2, 4, 6} x {1,3, 5, 7}
= {(2, 1), (2, 3), (2, 5), (2, 7), (4, 1), (4, 3), (4, 5), (4, 7), (6, 1), (6, 3), (6, 5), (6, 7)}

(iv) B x B = {2, 4, 6} x {2, 4, 6}
= {(2, 2), (2, 4), (2, 6), (4, 2), (4, 4), (4, 6), (6, 2), (6, 4), (6, 6)}

(v) n (A x A) = no. of distinct elements in A x A = 16

(vi) n (A x B) = n (A) x n (B) = 4 x 3 = 12

(vii) n (B x A) = n (B) x n (A) = 3 x 4 = 12

(viii) n (B x B) = n (B) x n (B) = 3 x 3 = 9

Que-4: Answer true or false :
(i) If P = {m, n} and Q = {m, n}, then P x Q = {(m, n), (n, m)}
(ii) {(a, x), (a, y), (b, x), (b, y)} is a product set.
(iii) If n (A) = x and n (B) = y and A ∩ B = Φ, then n (A x B) = xy.
(iv) If A and B are non-empty sets, then A x B is a non-empty set of ordered pairs (x, y) such that x ∈ B and y ∈ A.

Sol: (i) Given P = {m, n) and Q = {n, m}
∴ P x Q = {{m, n), (m, m), (n, n), (n, m)}
Thus, given statement is false.

(ii) Let A = {a, b} and B = {x, y}
∴ A x B = {{a, x), (a, y), (b, x), (b, y)} which is the cartesian product of set A and set B.
Thus given statement is true.

(iii) n (A x B) = n (A) x n (B) = xy
∴ given statement is true.

(iv) False, ∵ A x B = {(x, y); x ∈ A and y ∈ B}

Que-5: Given A = {1, 2}, B = {3}, C = {4, 5}, test whether the following are true :
(i) A x (B ∪ C) = (A ∪ B) x (A ∪ C)
(ii) A x (B ∩ C) = (A x B) ∩ (A x C).

Sol: Given A = {1, 2} ; B = {3} and C = {4, 5}

(i) L.H.S = A x (B ∪ C) = {1, 2} x {3, 4,5}
= {(1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5)}
Now A ∪ B = {1, 2, 3}
and A ∪ C = {1, 2, 4, 5}
∴ R.H.S = (A ∪ B) x (A ∪ C)
= {1, 2, 3} x {1, 2, 4, 5}
= {(1, 1), (1, 2), (1, 4), (1, 5), (2, 1), (2, 2), (2, 4), (2, 5), (3, 1), (3, 2), (3, 4), (3, 5)}
∴ L.H.S ≠ R.H.S
Thus given statement is not true.

(ii) ∴ B ∩ C = Φ
L.H.S = A x (B ∩ C) = {1, 2} x Φ = Φ
∴ A x B = {1, 2} x {3} = {(1, 3), (2, 3)}
A x C = {1, 2} x {4, 5} = {(1, 4), (1, 5), (2, 4), (2, 5)}
R.H.S. = (A x B) ∩ (A x C) = Φ
∴ L.H.S. = R.H.S
Thus given statement is true.

Que-6: If A = {1,2,3}, B = {3,4} and C = {4,5,6}, then find (A×B)∪(A×C)

Sol:  A = {1,2,3}, B = {3,4} and C = {4,5,6}
(A×B) = {(1,3), (1,4), (2,3), (2,4), (3,3), (3,4)}
(A×C) = {(1,4), (1,5), (1,6), (2,4), (2,5), (2,6), (3,4), (3,5), (3,6)}
(A×B)∪(A×C)
= {(1,3), (1,4), (1,5), (1,6), (2,3), (2,4), (2,5), (2,6), (3,3), (3,4), (3,5), (3,6)}

Que-7: If A = {1, 2, 3, 4}, B = {5, 7, 9}, C = {2, 4, 6}, find
(i) A x B
(ii) (B x C)
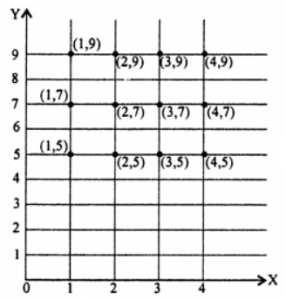
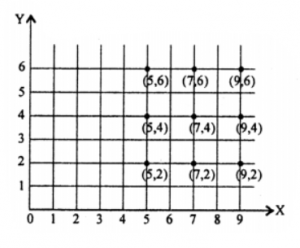
(iii) C X A and draw their graphs.

Sol: Given A = {1, 2, 3, 4} ; B = (5, 7, 9} and C = {2, 4, 6}
(i) A x B = {(1, 5), (1, 7), (1, 9), (2, 5), (2, 7), (2, 9), (3, 5), (3, 7), (3, 9), (4, 5), (4, 7), (4, 9)}

(ii) B x C = {5, 7, 9} x {2, 4, 6}
= {(5, 2), (5, 4), (5, 6), (7, 2), (7, 4), (7, 6), (9, 2), (9, 4), (9, 6)}

(iii) C x A = {2, 4, 6} x {1,2, 3, 4}
= {(2, 1), (2, 2), (2, 3), (2, 4), (4, 1), (4, 2), (4, 3), (4, 4), (6, 1), (6, 2), (6, 3), (6,4)}

Que-8: Some elements of A x B are (a, x), (c, y), (d, z). If A = {a, b, c, d], find the remaining elements of A x B such that n (A x B) is least.

Sol: Given A = {a, b, c, d}
Since some elements of A x B are (a, x), (c, y), (d, z)
Thus B must be taken as {x, y, z} s.t n (A x B) is least.
∴ A x B = {a, b, c, d) x {x, y, z} = {(a, x), (a, y), (a, z), (b, x), (b, y), (b, z), (c, x), (c, y), (c, z), (d, x), (d, y), (d, z)}
Thus remaining elements of A x B are {(a, y), (a, z), (b, x), (b, y), (b, z), (c, x), (c, z), (d, x), (d y)}

Que-9: The ordered pairs (1, 1), (2, 2), (3, 3) are among the elements in the set A x B. If A and B have 3 elements each, how many elements in all does the set A x B have ? Also find the remaining elements.

Sol: Given n (A) = 3 ; n (B) = 3
∴ n (A x B) = n (A) x n (B) = 3 x 3 = 9
Now (1,1), (2, 2), (3, 3) ∈ A x B
∴ first components of A x B i.e. 1, 2, 3 ∈ A
∴ A = {1, 2, 3} since A has exactly 3 elements and B = {1, 2, 3}
∴ A x B = {(x, y) : x ∈ A and y ∈ B}
= {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}
Thus remaining elements of A x B are {(1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2)}

Que-10: If A = {1, 4}, B = {2, 3, 6} and C = {2, 3, 7}, then verify that
(i) A x (B ∪ C) = (A x B) ∪ (A x C)
(ii) A x (B n C) = (A x B) ∩ (A x C)

Sol: Given A= {1, 4} ; B = {2, 3, 6} and C = (2, 3, 7}

(i) B ∪ C = {2, 3, 6} ∪ {2, 3, 7} = {2, 3, 6, 7}
L.H.S = A x (B ∪ C) = {1, 4} x {2, 3, 6, 7}
= {(1, 2), (1, 3), (1, 6), (1, 7), (4, 2), (4, 3), (4, 6), (4, 7)}
A x B = {1, 4} x {2, 3, 6} = {(1, 2), (1, 3), (1, 6), (4, 2), (4, 3), (4, 6)}
A x C = {1, 4} x (2, 3, 7} = {(1, 2), (1, 3), (1, 7), (4, 2), (4, 3), (4, 7)}
∴ R.H.S. = (A x B) ∪ (A x C)
= {(1, 2), (1, 3), (1, 6), (4, 2), (4, 3), (4, 6)} u {(1, 2), (1, 3), (1, 7), (4, 2), (4, 3), (4, 7)}
= {(1, 2), (1, 3), (1, 6), (1, 7), (4, 2), (4, 3), (4, 6), (4, 7)}
Thus L.H.S. = R.H.S.
∴ A x (B ∪ C) = (A x B) ∪ (A x C)

(ii) ∴ B ∩ C = {2, 3, 6} ∩ {2, 3, 7} = {2, 3}
L.H.S = A x (B ∩ C) = {1, 4} x {2, 3} = {(1, 2), (1, 3), (4, 2), (4, 3)}
R.H.S = (A x B) ∩ (A x C) = {(1, 2), (1, 3), (1, 6), (4, 2), (4, 3), (4, 6)} ∩ {(1, 2), (1, 3), (1, 7), (4, 2), (4, 3), (4, 7)}
= {(1, 2), (1, 3), (4, 2), (4, 3)}
∴ L.H.S = R.H.S
Thus A x (B ∩ C) = (A x B) ∩ (A x C)

Que-11: If A = {2, 3}, B = {1, 2, 3}, C = {2, 3, 4} show that A x A = (B x B) ∩ (C x C).

Sol: Given A = {2, 3} ; B = {1, 2, 3} and C = {2, 3, 4}
L.H.S = A x A = {2, 3} x {2, 3} = {(2, 3). (2, 3), (3, 2), (3, 3)}
Now B x B = {1, 2, 3} x {1,2,3}
= {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}
and C x C = {2, 3, 4} x {2, 3, 4}
= {(2, 2), (2, 3), (2, 4), (3, 2), (3, 3), (3, 4), (4, 2), (4, 3), (4, 4)}
∴ R.H.S = (B x B) ∩ (C x C)
= {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)} ∩ {(2, 2), (2, 3), (2, 4), (3, 2), (3, 3), (3, 4), (4, 2), (4, 3), (4, 4)} = {(2, 2), (2, 3), (3, 2), (3, 3)}
∴ L.H.S = R.H.S

Que-12: If A and B be two sets such that n (A) = 3 and n (B) = 2. If (x, 1), (y, 2), (z, 1) are in A x B, find A and B, where x, y, z are distinct elements.

Sol: Given n (A) = 3 and n (B) = 2
since, (x, 1), (y, 2), (z, 1) ∈ A x B
Since first components of A x B are in set A and second components are in set B.
Since x, y, z are given to be distinct elements.
∴ A = {x, y, z} similarly B = {1, 2}
Since A x B = {(x, y) : x ∈ A and y ∈ B}

Que-13: The Cartesian product A x A has 9 elements among which are found (- 1, 0) and (0, 1). Find the set A are the remaining elements of A x A.

Sol: Given n (A x A) = 9 ⇒ n (A) x n (A) = 9
⇒ n (A) = 3
Thus no. of distinct elements in set A be 3.
Now (- 1, 0), (0, 1) ∈ A x A
So first and second components of each ordered pair of A x A are belonging to A
∴ – 1, 0, 1 ∈ A
Thus A ={-1,0,1} and A x A = {- 1, 0, 1} x {- 1, 0, 1}
∴ A x A = {(- 1, – 1), (- 1, 0), (- 1, 1), (0, – 1), (0, 0), (0, 1), (1, – 1), (1, 0), (1, 1)}
Hence remaining elements of A x A are (- 1, – 1), (- 1, 1), (0, – 1), (0,0), (1, – 1), (1,0), (1, 1).

–: End Relation and Functions Class 11 OP Malhotra Exe-2A ISC Math Ch-2 Solutions :–

Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions

Thanks

Please share with your friends