Relations and Functions Class 11 OP Malhotra Exe-2F ISC Maths Solutions Ch-2 Solutions. In this article you would learn about Discussion on Domain and Range of Function. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Relations and Functions Class 11 OP Malhotra Exe-2F ISC Maths Solutions Ch-2

Board	ISC
Publications	S Chand
Subject	Maths
Class	11th
Chapter-2	Relations and Functions
Writer	OP Malhotra
Exe-2(F)	Discussion on Domain and Range of Function

Exercise- 2F

Relations and Functions Class 11 OP Malhotra Exe-2F Solution.

Que-1: The range and domain of function f(x) = (3/x) + 1 are subsets of A and B respectively,
where A = {(−1/2), 0, (2/3), (6/7), 1}
and B = {−5, 0, {4*(1/2)}, 5, {5*(1/2)}}.
List the elements of the function as ordered pairs.

Sol: Given function f(x) = (3/x) + 1
f(-1/2) = {3/(-1/2)} + 1 = -6+1 = -5 ∈ B
∴ {(-1/2), -5} ∈ f
Further f(0) does not exists
f(2/3) = {3/(2/3)} + 1 = 11/2 ∈ B
∴ {(2/3), (11/2)} ∈ f
f(6/7) = {(3×7)/6} + 1 = 9/2 ∈ B
∴ {(6/7), (9/2)} ∈ f
f(1) = 3 + 1 = 4 ∉ B
∴ f = [{(-1/2), -5}, {(2/3), (11/2)}, {(6/7), (9/2)}]

Que-2: A = {- 2, – 1, 1, 2} and f = [{x, (1/x)}, x ∈ A]
(i) List the domain of f
(ii) List the range off
(iii) Is f a function ?

Sol: Given f be a function defined by
f(x) = 1x ∀ x ∈ A
where A = {- 2, – 1, 1, 2}
∴ f(- 2) = – 12 ; f(- 1) = – 1 ∈ A
f(1) = 1 ∈ A; f(2) = 12
Thus f = {(−1,−1), (1,1), (−2, (−1/2)), (2,(1/2))}
Domain (f) = {- 1, 1, – 2, 2}
Range (f) = {- 1, 1, (–1/2), (1/2)}
Since each element in domain of f has unique image, i.e. no two ordered pairs have same first component.
∴ f represents a function.

Que-3: f : A → highest prime factor of x.
(i) Find the range off when the domain is {12, 13, 14, 15, 16, 17}.
(ii) State a domain of five integers for which the range is (3).
(iii) A set of positive integers is called S. What can be said about these integers iff(S) = S?

Sol: Given f : x → highest prime factor of x

(i) Here factors of 12 are 1, 2, 3, 4, 6, 12
∴ 3 be the highest prime factor of 12.
∴ 3 ∈ R_f
Also, factors of 13 are 1 and 13
∴ 13 be the highest prime factor of 13
∴ 13 ∈ R_f
Since 1, 2, 7, 14 are the factors of 14
∴ 7 be the highest prime factor of 14.
∴ 7 ∈ R_f
Since 1, 3, 5, 15 are the factors of 15
Here 5 be the highest prime factor of 15
∴ 5 ∈ R_f
Since 1, 2, 4, 8 and 16 are the factors of 16
Here 2 be the highest prime factors of 16
∴ 2 ∈ R_f
Since 1, 17 are factors of 17. Here 17 be the highest prime factor of 17.
∴ 17 ∈ R_f
∴ range (f) = {2, 3, 5, 7, 13, 17}

(ii) given R_f = 3 i.e. highest prime factor of each element of domain of f be 3.
Since 3 be the highest prime factor of 3, 6, 9, 12, 18 [since highest prime factor of 15 be 5]
∴ Required D_f = {3, 6, 9, 12, 18}

(iii) Given f(S) = S i.e. highest prime factors of S is equal to S which is only possible if S be the set of all prime numbers. Since factors of any prime number p are 1 and p. So p be the highest prime factor of p.

Que-4: A function f is defined on the set of integers as follows :

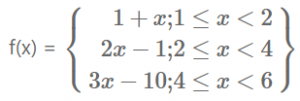
(i) Find the domain of the function
(ii) Find the range of the function
(iii) Find the value of f(4).

Sol: (i) since f is defined on set of integers.
Clearly f(x) has different values for all 1 ≤ x ≤ 6
∴ x = 1, 2, 3, 4, 5
Thus Df = {1, 2, 3, 4, 5}.

(ii) When x = 1, f(1) = 1 + 1 = 2
When x = 2, f(2) = 2 x 2 – 1 = 3
When x = 3, f(x) = 2x – 1 ⇒ f(3) = 6 – 1 = 5
When x = 4, f (x) = 3x – 10 ⇒ f(4) = 3x – 10 = 2
When x = 5,f (x) = 3x – 10 ⇒ f(5) = 15 – 10 = 5
∴ Rf = {2, 3, 5}

(iii) When x = 4, f(x) = 3x – 10
∴ f(4) = 3 x 4 – 10 = 2

Que-5: Let f be a function whose domain is the set of all real number. If f(x) = | x | – x, what is range off?

Sol: Given f(x) = | x | – x since | x | ≥ x ∀ x ∈ D_f
∴ | x | – x ≥ 0 ⇒ f(x) ≥ 0
∴ R_f = [0, ∞)

Que-6: Write the domain of the following real functions
(i) f(x) = {x²+2x+1}/{x²-x-6}
(ii) √(1−2x−3x²)
(iii) f(x) = {x³-x+3}/{x²-1}
(iv) 1/√{x²−7}
(v) log (2 – 3x)
(vi) log(√(x-4) + √(6-x))
(vii) [log10{(5x−x²)/4}]^(1/2)
(viii) sin¯¹[log2(x/2)]

Sol: (i) Given : f(x) = {x²+2x+1}/{x²-x-6}
f(x) is defined if x2 – x – 6 ≠ 0
⇒ x2 – 3x + 2x – 6 ≠ 0
⇒ (x – 3)(x + 2) ≠ 0
⇒ x ≠ – 2, x ≠ 3
So, the domain of f(x) = R – {– 2, 3}

(ii) √(1−2x−3x²)
1−2x−3x² ≥ 0
−3x²-2x+1 ≥ 0
3x²+2x-1 ≤ 0
x = {−b±√(b²−4ac)}/2a
where a=3, b=2, and c=−1.
Calculating the discriminant:
b²−4ac = 2²−4⋅3⋅(−1) = 4+12 = 16
Now substituting into the quadratic formula:
x = {−2±√(16}/{2⋅3} = (−2±4)/6
This gives us two solutions:
1. x = (−2+4)/6 = 2/6 = 1/3
2. x = (−2−4)/6 = −6/6 = −1
Domain = {-1 ≤ x ≤ (1/3)}

(iii) For real value of x2 – 1 ≠ 0
⇒ (x – 1)(x + 1) ≠ 0
⇒ x – 1 ≠ 0 or x + 1 ≠ 0
⇒ x ≠ 1 or x ≠ –1
Therefore, the domain of f = R – {–1, 1}

(iv) Let f(x) = 1/√(x²-7)
For Df : f(x) must be a real number.
⇒ 1/√(x²-7) must be a real number.
⇒ x² – 7 > 0 ⇒ |x| > √7
⇒ x > √7 or x < – √7
⇒ x ∈ (- ∞, – √7) ∪ (√7, ∞)
∴ Df = (- ∞, – √7) ∪ (√7, ∞)

(v) Let f (x) = log (2 – 3x)
For Df : f(x) must be a real number.
⇒ log (2 – 3x) must be a real number.
⇒ 2 – 3x > 0 ⇒ 2 > 3x ⇒ 3x < 2
⇒ x < 2/3
∴ Df = (- ∞, (2/3))

(vi) Let f = f(x) = log (√(x-4) + √(6-x))
For Df : f(x) must be a real number
⇒ log (√(x-4) + √(6-x)) must be a real number.
⇒ √{(x-4) + √(6-x)} > 0
⇒ x – 4 ≥ 0 and 6 – x ≥ 0
⇒ x ≥ 4 and 6 ≥ x
⇒ 4 ≤ x < 6 ⇒ x ∈ [4, 6]
∴ Df = [4, 6]

(vii) [log10{(5x−x²)/4}]^(1/2)
For D_f : f(x) must be a real number.

5x-x² ≥ 4
x²-5x+4 ≤ 0
(x-1)(x-4) ≤ 0
1 ≤ x ≤ 4
x ∈ {1, 4}.

(viii) sin¯¹[log2(x/2)]
We know that sin-1 y is defined for – 1 ≤ y ≤ 1
∴ f(x) is defined only
if – 1 ≤ log2 (x/2) ≤ 1 and (x/2) > 0
⇒ 2¯¹ ≤ x2 ≤ 2¹ and x > 0
⇒ (1/2) x 2 ≤ x ≤ 4 and x > 0
⇒ 1 ≤ x ≤ 4 and x > 0
⇒ 1 ≤ x ≤ 4 ⇒ x ∈[1, 4]
∴ Df = [1, 4]

Que-7: Find the range of each of the following function
(i) |x – 3|
(ii) √x-5
(iii) cos(x/3)
(iv) x+2/|x+2|
(v) sec{(π/4)cos²x},  – ∞ < x ∞
(vi) (x²+x+2)/(x²+x+1); x ∈ R
(vii) x/(1+x²)
(viii) f(x) = 3/(2−x²)
(ix) f(x) = 1/(2-cos3x)

Sol: (i) Let y = f(x) = | x – 3 | if defined for all x ∈ R
∴ Df = R = (- ∞, ∞)
For Rf since | x | ≥ 0 ∀ x ∈ R
⇒ |x – 3| ≥ 0 ∀ x ∈ R
⇒ f(x) ≥ 0 ∀ X ∈ R
∴ Rf = [0, ∞)

(ii) y = f(x) = √(x-5)
For Df : f(x) must be a real number.
⇒ √(x-5) must be a real number.
⇒ x – 5 ≥ 0
⇒ x ≥ 5
∴ Df = [5, ∞)
For Rf : Let y = f(x) = √(x-5) ∀ x ∈ Df
∴ y ≥ 0 [since square root of a real no. is always non-negative]
⇒ y² = x – 5 ⇒ x = y² + 5
since x ≥ 5 ⇒ y² + 5 ≥ 5
⇒ y² ≥ 0 ∀ y ∈ R
∴ Rf = [0, ∞)

(iii) Let y = f(x) = cos(x/3)
Here f(x) is defined for all x ∈ R
∴ Df = R
For Rf : since – 1 ≤ cos z ≤ 1 ∀ z ∈ R
⇒ -1 ≤ cos (x/3) ≤ 1
⇒ – 1 ≤ y ≤ 1
∴ Rf = [- 1, 1]

(iv) Given f(x) = (x+2)/|x+2|
For Df : f(x) must be a real number.
⇒ (x+2)/|x+2| must be a real number
⇒ x + 2 ≠ 0 ⇒ x ≠ – 2
∴ Df = R – {- 2}
For Rf : Let y = (x+2)/|x+2| ∀ x ∈ Df
Case-I : When x < – 2 ⇒ x + 2 < 0 ∴ | x + 2 | = – (x + 2) ∴ y = (x+2)/−(x+2) = 1 [ ∵ x ≠ – 2] Case-II : When x > – 2 ⇒ x + 2 > 0
⇒ | x + 2 | = x + 2
∴ y = (x+2)/(x+2) = 1 [ ∵ x ≠ – 2]
Hence, Rf = {- 1, 1}

(v) Let y = f (x) = sec {(π/4)cos²x}
since 0 ≤ cos²x ≤ 1
0 ≤ (π/4)cos²x ≤ π/4
sec 0 ≤ sec(π/4)cos²x ≤ sec (π/4)
1 ≤ f(x) ≤ √2
Rf = [1, √2].

(vi) Let y = f (x) = {x²+x+2}/{x²+x+1}, x ∈ R
Clearly, f(x) is defined for all x ∈ R
So, domain (f) = R. Let f(x) = y Then,
{x²+x+2}/{x²+x+1} = y
⇒ x²(y−1)+(y−2) ≥ 0
Also, y≠1 for any x ∈ R.
Hence range of f(x) = [1, (7/3)]

(vii) y = f(x):
y = x/(1+x²)
y(1+x²) = x ⟹ y + yx² = x ⟹ yx²−x+y = 0
yx²−x+y = 0
Here, a=y, b=−1, and c=y.
D = b²−4ac = (−1)² − 4(y)(y) = 1 − 4y²
Set the discriminant D≥0:
1 − 4y² ≥ 0
4y² ≤ 1 ⟹ y² ≤ 1/4
(−1/2) ≤ y ≤ (1/2)
Range = {(-1/2), (1/2)}.

(viii) Set f(x) = y:
y = 3/(2−x²)
y(2−x²) = 3
⟹ 2y − yx² = 3
⟹ yx² = 2y−3
⟹ x² = (2y−3)/y
(2y−3)y ≥ 0
– Case 1: y > 0 and 2y−3 ≥ 0:
– This implies 2y ≥ 3 or y ≥ 3/2.
– Case 2: y < 0 and 2y−3 < 0:
– This is always true since 2y < 0 implies y < 0.
– y < 0 (which corresponds to negative values)
– y ≥ 3/2 (which corresponds to values greater than or equal to 3/2)
Therefore, the range of f(x) is:
Range = (−∞, 0) ∪ {(3/2), ∞)}

(ix) −1 ≤ cos(3x) ≤ 1
Next, we will manipulate the inequality to find the range of 2−cos(3x):
2−1 ≤ 2−cos(3x) ≤ 2−(−1)
This simplifies to:
1 ≤ 2−cos(3x) ≤ 3
(1/3) ≤ 1/(2−cos(3x)) ≤ 1
This means:
1/(2−cos(3x)) will range from (1/3) to 1
Since y = 1/(2−cos(3x)), we can conclude that:
1/3 ≤ y ≤ 1
Range = [(1/3), 1]

Que-8: Find the domain and range of the function (x²-4)/(x-2)

Sol: Let y = f(x) = (x²−4)/(x−2)
For Df : f(x) must be a real number.
⇒ (x²−4)/(x−2) must be a real number.
⇒ x – 2 ≠ 0 ⇒ x ≠ 2
∴ Df = R – {2}
For Rf : (x²−4)/(x−2) ∀ x ∈ Df i.e. x ≠ 2
⇒ y = {(x−2)(x+2)}/{x−2) = x + 2 [∵ x – 2 ≠ 0]
⇒ x = y – 2
Since x ∈ Df ⇒ x ≠ 2 ⇒ y – 2 ≠ 2 ⇒ y ≠ 4
∴ Rf = R – {4}

Que-9: If the domain of the function (|x|)/x be [3, 7], then its range is
(a) [- 1, 1]
(b) [- 1, 1]
(c) {1}
(d) {- 1}

Sol: Given domain of function f (x) = |x|/x be [3, 7].
∴ 3 ≤ x ≤ 7 ⇒ | x | = x
Thus, f(x) = |x|/x = x/x = 1 [∵ x ≠ 0 and x > 0]
∴ Rf = {1}

–: End Relation and Functions Class 11 OP Malhotra Exe-2F ISC Math Ch-2 Solutions :–

Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions

Thanks

Please share with your friends