Relations and Functions Class 11 OP Malhotra Exe-2G ISC Maths Solutions Ch-2 Solutions. In this article you would learn about Graph of Real, Absolute and Exponential Functions. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Relations and Functions Class 11 OP Malhotra Exe-2G ISC Maths Solutions Ch-2

Board	ISC
Publications	S Chand
Subject	Maths
Class	11th
Chapter-2	Relations and Functions
Writer	OP Malhotra
Exe-2(G)	Graph of Real, Absolute and Exponential Functions.

Exercise- 2G

Relations and Functions Class 11 OP Malhotra Exe-2G Solution.

Graph Each Function.

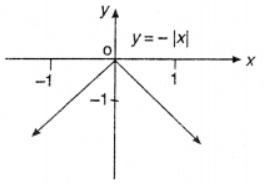
Que-1: y = – | x |

Sol: Given y = – | x |
Its domain is set of all real numbers and range is set all negative numbers including 0.
since | x | > 0 ⇒ – | x | < 0 ⇒j<0 When x > 0 ; y = – x [∵ | x | = x]
which is the eqn. of straight line passing through (0, 0) making a slope of – 1.
When x < 0 ; y = x [∵ | x | = x]
which is the eqn. of straight line having slope = 1.
The graph of y = – | x | is given as under ;

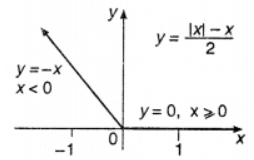
Que-2: y = {|x|-x}/2

Sol: Given : y = {|x|-x}/2
Here domain of function is set of all real numbers.
When x ≥ 0 ∴ |x| = x ⇒ y = (x−x)/2 = 0
which shows the x-axis.
When x < 0 ∴ | x I = – x
⇒ y = (−x−x)/2 = – x
which is the eqn. of straight line having slope – 1.

Que-3: y = 1/|x|

Sol: Given : y = 1/|x|
Here domain of the function is the set of all non-zero real numbers.
Further the graph does not meet coordinate axes.
When x ≥ 0 ∴ |x| = x ⇒ y = 1/x
When x < 0 ⇒ | x | = – x
∴ y = –1/x

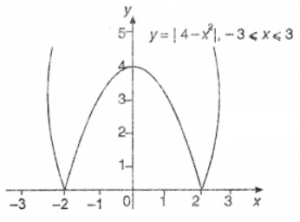
Que-4: y = | 4 – x² |, – 3 ≤ x ≤ 3.

Sol: Given y = | 4 – x² |, – 3 ≤ x ≤ 3
Here D_f = R and range (f) = [0, ∞)
When – 3 < x < – 2
⇒ x + 2 < 0 and 2 – x > 0
∴ y = | 2 – x | | 2 + x | = – (2 – x) (x + 2)
y = – (4 – x²) = x² – 4 ⇒ x² = y + 4
which represents an upward parabola with vertex (0, – 4)
When – 2 ≤ x ≤ 2
⇒ x – 2 ≤ 0 and x + 2 ≥ 0
∴ y = (2 – x) (2 + x) = 4 – x² ⇒ x² = 4 – y
⇒ x² = – (y – 4) which represents a downward parabola with vertex (0, 4) meeting x-axes at (± 2, 0),
When 2 < x ≤ 3 ⇒ 2 – x < 0, 2 + x > 0
∴ y = – (2 – x) (2 + x) = – (4 – x² )
⇒ x² – 4 = v
⇒ x² = 4 + y which is again represents a downward parabola with vertex (0, – 4).
Thus the required graph of given function is given as under :

Que-5: y = | x | + x, – 2 ≤ x ≤ 2

Sol: Given y = | x | + x, – 2 ≤ x ≤ 2
Here domain of function is set of all real numbers.
When – 2 ≤ x < 0 ∴ |x| = – x
⇒ y = – x + x = 0
which is the eqn. of x-axis.
When 0 ≤ x < 2 ∴ | x | = x
⇒ y = x + x = 2x
which is the eqn. of straight line passing through (0, 0) with slope 2.

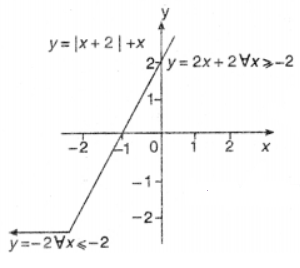
Que-6: y = |x + 2| + x

Sol: Here domain of the function is the set of all real numbers.
Case – I: When x ≤ – 2 ∴ x + 2 ≤ 0
⇒ | x + 2 | = – (x + 2)
∴ y = – (x + 2) + x = – 2
Hence the graph is left side of the line y = – 2 for x ≤ – 2

Que-7: (i) Copy and complete this table of values :
(ii) Draw the graph y = 3^x on squared paper, for – 2 ≤ x ≤ 3.
(iii) What features do the graphs of y = 2^x (drawn on page Ch 2-51) and y = 3^x have in common?

Sol: (i) Giveny = 3^x
When x = 1 ⇒ y = 3
When x = 2 ⇒ y = 3² = 9
When x = 3 ⇒ y = 3³ = 27
The table of values becomes ;

(ii) When x → ∞ ⇒ y → ∞
When x → ∞ ⇒ 3^-∞ → 0 ⇒ y → 0

(iii) Clearly both graphs pass through the point (0, 1) rise steadily from left to right. Also x-axis be the tangent to both graphs at infinity.
Further both graphs as x → ∞ ⇒ x → ∞ as x → – ∞ ⇒ y → 0

Que-8: (i) Copy and complete this table.

(ii) Draw the graphs y = 2^x (See Solved Ex. 68) and y = (1/2)^x , on the same diagram, for – 3 ≤ x ≤ 3.
(iii) Which line is the axis of symmetry in the diagram?

Sol: (i) y = (1/2)^x
When x = – 2 ⇒ y = (1/2)^¯² = 2² = 4
When x = – 1 ⇒ y = (1/2)¯¹ = 2
When x = 1 ⇒ y = 1/2
The table of values is given as under:

(ii) When x → ∞ ⇒ y → 0
When x → ∞ ⇒ y → ∞
For graph of y = 2^x :
The table of values is given as under

as x → ∞ ⇒ y → ∞
and as x → – ∞ ⇒ y → 0

(iii) Clearly both graphs lies in first and second quadrants and intersecting at point (0, 1).
Further y-axis is the required line of symmetry.

Que-9: A sketch of the graph y = a log₄ (x + b) is shown in Fig. 2.78. Find the values of a and b.

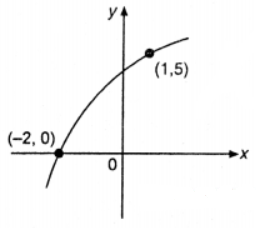
Sol: Given y = alog₄(x + b) …(1)
Clearly the graph of eqn. (1) pass through the points (- 2, 0) and (1, 5).
Thus, 0 = a log₄ (b – 2)
since a ≠ 0 ∴ 0 = log₄ (b – 2)
⇒ 4° = b – 2 ⇒ 1 = b – 2 ⇒ b = 3
Also, 5 = a log₄ (1 + b) ⇒ 5 = a log₄ 4
⇒ 5 = a x {(log4)/(log4)}
a = 5.

Que-10: Diagrams (i) shows the curve y = log_a x. What is the value of a ?

Sol: Given eqn. of curve be
y = log_a x …(1)
Since, eqn. (1) passes through the point (81, 4).
⇒ 4 = log_a 81
⇒ a⁴ = 81 = 3⁴
⇒ a = 3 [if x = log_a y ⇒ a^x = y]

Que-11: Diagram given below (ii) shows the curve y = log₁₀ (x + p). What is the value of p ?

Sol:  Given eqn. of curve be
y = log₁₀ (x + P) … (1)
Clearly graph of eqn. (1) pass through the point (- 1, 0).
∴ 0 = log₁₀ (- 1 + p) ⇒ 10⁰ = – 1 + p
⇒ p = 1 + 1 = 2

Que-12: (i) Sketch the graphs y = 2
and y = log₁₀ 2x on the same diagram.
(ii) Find the point of intersection of the graphs by solving the equation log10 2x = 2.

Sol: (i) Given y = 2 which is the eqn. of straight line passing through (0, 2) and || to x-axis.
Also given y = log10 2x ⇒ 2x = 10y
⇒ x = (1/2).10y
Here domain of the function Df = (0, ∞)
The table of values is given as under:

(ii) Given log₁₀ 2x = 2 … (1)
We know that if log_a x = y ⇒ a^y = x
∴ from (1) ; 2x = 10² ⇒ 2x = 100
⇒ x = 50
Hence both graph intersects at (50, 2).

Que-13: The sketch shows part of the graph
y = a log₂ (x – b).
Find the values of a and b.

Sol: Given equation of curve be
y = a log₂ (x – b) …(1)
Clearly from graph given, it is observed that eqn.(1) passes through the points (5,0) and (6,3).
∴ 0 = a log₂ (5 – b)
since a ≠ 0 ∴ 0 = log₂ (5 – b) ⇒ 5 – b = 2°
⇒ 5 – b = 1 ⇒ b = 4
Also, 3 = a log₂ (6 – b) ⇒ 3 = a log₂ (6 – 4)
⇒ 3 = a log₂ 2 ⇒ a = 3 [∵ log_a a = 1]
Hence, a = 3 and b = 4

Que-14: (i) Sketch the graphs y = 4 – x and y = log₁₀ x on the same diagram.
(ii) Write down an equation to find the x-coordinate of the point of inter-section of the graphs.
(iii) Show that x satisfies 3.4 < x < 3.5.
(iv) From your graph find x, correct to 2 decimal places.

Sol: (i) eqn. of given curve be y = 4 – x
Hence the given curve meets x-axis at (4, 0) and y-axis at (0, 4).
Also eqn. of another curve be
y = log₁₀ x ⇒ x = 10^y
Here domain of the function is the set of all positive real numbers i.e. D_f = (0, ∞).

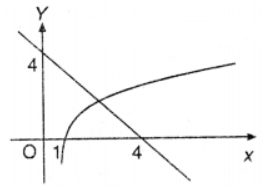
(ii) Both curves intersects when 4 – x = log₁₀x
which is the required equation which gives the x-coordinate of point of intersection given graphs.

(iii) Since 4 – x = log₁₀x …(1)
⇒ f(x) = log₁₀ x + x – 4
Now f(3.4) = log₁₀ (3.4) + 3.4 – 4 = 0.5314 – 0.6 = – 0.0685
f(3.5) = log₁₀ (3.5) + 3.5 – 4 = 0.044068
Thus root of eqn. (1) lies between 3.4 and 3.5
i.e. x satisfies 3.4 < x < 3.5
Also given y = log₁₀ 2x ⇒ 2x = 10^y
⇒ x = (1/2).10^y
Here domain of the function D_fy = (0, ∞)
The table of values is given as under:

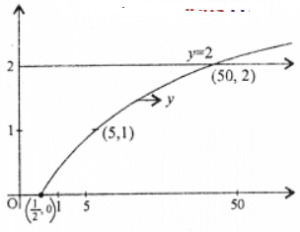
(iv) Given log₁₀2x = 2 …(1)
We know that if log_a x = y ⇒ a^y = x
∴ from (1) ; 2x = 10² ⇒ 2x = 100
⇒ x = 50
Hence both graph intersects at (50, 2).

Que-15: Sketch the graphs.
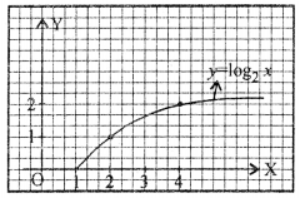
(i) y = log₂ x
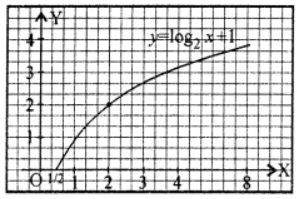
(ii) y = log₂ x + 1
(iii) y = log₂ (x + 1)

Sol: (i) Given eqn, of curve be
y = log₂ x ⇒ x = 2^y
Here domain of given function is the set of all positive real numbers.
as y → ∞ ⇒ x → ∞
as y → ∞ ⇒ x → ∞

(ii) Given eqn. of curve be
y = log₂ x + 1 ⇒ y – 1 = log₂ x
⇒ x = 2^y-1 = (1/2).2^y
Here domain of function is set of all positive real numbers.
as x → ∞ ⇒ y → ∞
as x → 0 ⇒ y → – ∞

(iii) Given eqn. of curve be y = log₂ (x + 1)
⇒ 2^y = x + 1 ⇒ x = 2^y – 1
For D_f : x + 1 > 0 ⇒ x > – 1
∴ domain of function f = (- 1, ∞)
as x → ∞ ⇒ y → ∞

Que-16: Sketch the graphs.
(i) log₄ x
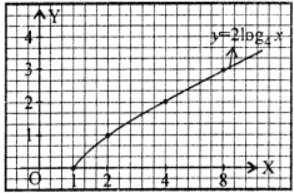
(ii) 2 log₄ x
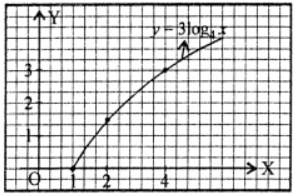
(iii) 3 log₄ x

Sol: (i) Given eqn. of curve be
y = log₄ x ⇒ x = 4^y
Here domain of the function is the set of all positive real numbers.
as x → ∞ ⇒ y → ∞
as x → 0 ⇒ y → – ∞

(ii) Given eqn. of curve be
y = 2 log₄ x ⇒ 4^y/2 = x
Here domain is again set of all positive real numbers
as x → ∞ ⇒ y → ∞
as x → 0 ⇒ y → – ∞

(iii) Given eqn. of curve be
y = 3 log₄ x ⇒ x = 4^y/3
Here domain of given function = (0, ∞).
as x → ∞ ⇒ y → ∞
as x → 0 ⇒ y → – ∞

Que-17: For – 2 < x< 1, draw the graph of y = 2^x.
(use 1 cm = 1 unit on both axes).
Use this graph to solve 2^x = 2x.

Sol: Given eqn. of curve be
y = 2^x, – 2 < x < 1
Here domain is set of all reals.
The given eqn. 2^x = 2x …(1)
be the intersection of lines y = 2^x and y = 2x
From graph it is follows that x = 1, 2 satisfies eqn. (1).

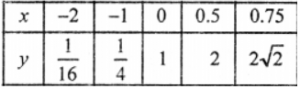
Que-18: (i) Complete the following table for y = 4^x.
Enter the values of x and y correct to 1 decimal place.
Copy the table on your answer book and enter the values there.
(ii) Taking 4 cm = 1 unit on both axes, draw the graph of y = 4^x for 0.75 ≥ x ≥ – 2.
(iii) From your graph estimate log₄ 1.25.

Sol: Given equation of curve be y = 4^x
When x = -2  = y = 4¯² = 1/16
When x = -1  = y = 4¯¹ = 1/4
When x = 0  = y = 4^0 = 1
When x = 1/2  = y = 2
When x = 3/4  = y = 4^(3/4) = 2√2


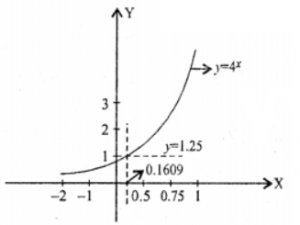
Further x → ∞ ⇒ y → ∞
and x → – ∞ ⇒ y → 0
since y = 4^x ⇒ x = log₄ y
i.e. when y = 1.25 it is observed from graph that x = 0.1609

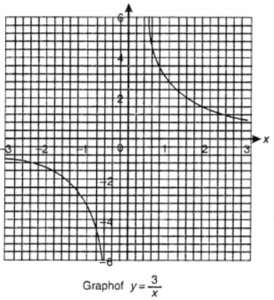
Que-19: Copy and complete the table, for the function y = (3/x), giving your answer correct to 1 d.p. Then draw and graph.

Sol:

Que-20: Sketch the graphs of the following rational functions
(i) y = (x+3)/(x−2)
(ii) y = 6/(x−6)
(iii) y = 5/(2x+1)
(iv) y = (2x+1)/(x−3)
(v) y = (7−2x)/(3x+5)

Sol: (i) Given eqn. of curve be y = (x+3)/(x−2)
∴ the function exists for x ≠ 2.
⇒ (x – 2) y = x + 3 ⇒ x (y – 1) = 3 + 2y ⇒ x = (3+2y)/(y−1)
∴ given function exists for y ≠ 1.
Thus x = 2 be the vertical asymptote and y = 1 be the horizontal asymptote. Also given curve meets x-axis at (-3, 0) and y-axis at (0, – 3/2).

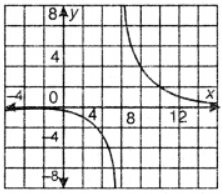
(ii) Given eqn. of curve be y = 6/(x−6). Thus the given function does exists for x + 6 ∴ x = 6 be the vertical asymptote.
Further xy – 6y = 6
⇒ xy = 6y + 6
⇒ x = (6y+6)/y
∴ given function exists for y ≠ 0
∴ y = 0 be the horizontal asymptote.

(iii) Given y = 5/(2x+1) ⇒ (2x + 1)y = 5
⇒ 2xy = 5 – y ⇒ x = (5−y)/xy
Thus given function exists for 2x + 1 ≠ 0 i.e. x ≠ – 1/2
∴ x = – 1/2 be the vertical asymptote to given curve.
Also function exists for y ≠ 0
∴ y = 0 i. e. x-axis be the horizontal asymptote. Clearly the curve meets y-axis at (0, 5) and curve does not meet x-axis.

(iv) Given eqn. of curve be y = (2x+1)/(x−3). Thus function exists for x ≠ 3
Also, xy – 3y = 2x + 1
⇒ x (y – 2) = 1 + 3y
⇒ x = (1+3y)/(y−2)
∴ given function exists for y ≠ 2
∴ x = 3 be the vertical and y = 2 be the horizontal asymptote. Further given curve meets coordinate axis at (-1/2, 0) and (0, –1/3).

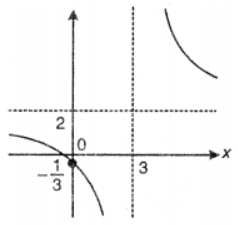
(v) Given eqn. of curve be y = (7−2x)/(3x+5)
Thus, given function exists for x ≠ –5/3
∴ x = – 5/3 be the vertical asymptote.
Also 3xy + 5y = 7 – 2x
⇒ x = (7−5y)/(3y+2)
∴ given function exists for y ≠ – 2/3
∴ y = 2/3 be the horizontal asymptote. Further, given curve
meets coordinate axes at (7/2, 0) and (0, 7/5).

–: End Relation and Functions Class 11 OP Malhotra Exe-2G ISC Math Ch-2 Solutions :–

Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions

Thanks

Please share with your friends