Sets Class 11 OP Malhotra Exe-1C ISC Maths Solutions Ch-1 Latest editions. In this article you would learn about Universal Set and Venn Diagrams. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Sets Class 11 OP Malhotra Exe-1C ISC Maths Solutions Ch-1 Latest editions
| Board | ISC |
| Publications | S Chand |
| Subject | Maths |
| Class | 11th |
| Chapter-1 | Sets |
| Writer | OP Malhotra |
| Exe-1(C) | Universal Set and Venn Diagrams |
Exercise- 1C
Sets Class 11 OP Malhotra Exe-1C ISC Maths Solutions Ch-1 Latest editions.
Que-1: Suggest a universal set for each of the following :
(i) {Jaipur, Chennai, Bangalore, Itanagar}
(ii) {Narmada, Cauvery, Mahanadi, Jhelum}
(iii) {Asia, Europe, Antarctica}
(iv) {Earth, Mars, Venus}
(v) {0, 5, 10, 15, 20, 25}
Sol: (i) Since given set consist of elements which are state capitals of India.
∴ Universal set – {state capitals of India}
(ii) elements of given sets are rivers of India
∴ Universal set = {Rivers of India}
(iii) elements of given sets are continents
∴ Universal set can be taken as {continents}
(iv) each element of given set be a planet of our solar system
∴ Universal set can be taken as :
{planets of our solar system}
(v) given set containing some multiples of 5.
∴ Universal set = {x : x = 5p, p ∈ W, 0 ≤ p ≤ 10}
Que-2: What universal set may be proposed for the following sets?
(i) The set of parallelograms
(ii) The set of irrational numbers
(iii) The set of positive even numbers
Sol: (i) given set be a set of all parallelograms
∴ Universal set can be taken as set of all quadrilaterals.
since every parallelogram is a quadrilateral.
(ii) Since real numbers consists of rational and irrational numbers.
Hence universal set can be taken as set of all real numbers.
(iii) Since set of all natural numbers consist of all positive even numbers.
∴ Universal set can be taken as set of all natural numbers.
Que-3: Solve the following equations :
(i) {x | 2x + 6 = 0, x ∈ Z}
(ii) {x | 5x + 16 = 1, x ∈ N}
(iii) {x | 2x – 3 < 7, x ∈ W}
(iv) {x | 4x – 25 > 13, x ∈ W}
(v) { y|(5y/3) – 7 ≤ 13, y is a prime number}
Sol: (i) Given 2x + 6 = 0 and x ∈ Z
∴ 2x = – 6 ⇒ x = – 3
∴ Soln. of given set = {- 3}
(ii) Given x ∈ N, 5x + 16 = 1 ⇒ 5x = – 15 ⇒ x = – 3 ∉ N
∴ Solution set = Φ
(iii) Given 2x – 3 < 7 ⇒ 2x < 10 ⇒ x < 5, x ∈ W
∴ x = 0, 1, 2, 3, 4 Thus solution set = {0, 1, 2, 3, 4}
(iv) Given 4x – 25 > 13 ⇒ 4x > 38
⇒ x > 38/4 = 19/2 and x ∈ Z
∴ x = 10, 11, 12, ………
Thus solution set = {10, 11, 12, ….}
(v) Given (5y/3) – y ≤ 13
⇒ (5y/3) ≤ 20 ⇒ 5y ≤ 60
⇒ y < 20 and y is a prime number
∴ y = 2, 3, 5, 7, 11, 13, 17, 19
Thus solution set = {2, 3, 5, 7, 11, 13, 17, 19}.
Que-4: ξ = {[−2*(1/2)], −1, √2, 3.5, √30, √36}
X = {integers}, Y = {irrational numbers}
List the members of (i) X (ii) Y
Sol: ξ = {[−2*(1/2)], −1, √2, 3.5, √30, √36}
(i) Given X = {integers} = {-1, √36} = {-1, 6}
(ii) Given Y = {irrational numbers} = {√2, √30}.
Que-5: ξ = {40, 41, 42, 43, 44, 45, 46, 47, 48, 49}
A = {prime numbers}, B = {odd numbers}
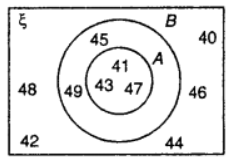
Place the ten numbers in the correct places on the diagram.
Sol: Given ξ = {40, 41, 42, 43, 44, 45, 46, 47, 48, 49}
A = {prime numbers = {41, 43, 47}
and B = {odd numbers} = {41, 43, 45, 47, 49}
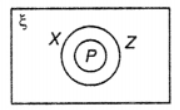
Que-6: X = {all triangles}, P = {isosceles triangles}, Z = {equilateral triangles}, Draw a Venn diagram to illustrate the relationship between these sets.
Sol: Given X = {all triangles}
P = {isosceles triangles}
Z = {equilateral triangles}
Clearly P ⊂ X, Z ⊂ X, Also every equilateral triangle be an isosceles
∴ P ⊂ Z
Que-7: Draw a Venn diagram to show the relationship between the following sets :
ξ = {quadrilaterals}, A = {parallelograms}, B = {rectangles}, C = rhombuses
Show in your diagram the region that represents the set of squares.
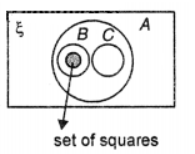
Sol: Given ξ = {quadrilaterals}
A = {parallelograms}
B = {rectangles} set
C = {rhombuses}
Since every rectangle, rhombus, square in a plane is a parallelogram. Further every square is a rectangle.
Que-8: Using ξ = {books}, N = {novels} and D = {detective novels}, represent the following statement as a Venn diagram, ‘Some novels are not detective novels.
Sol: Given ξ = {books}
N = {Novels}
D = {detective novels}
shaded portion represents the non-detective novels.
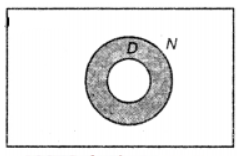
Que-9: Answer true or false. Refer Fig 1.7 .
(i) A ⊂ D
(ii) B ⊂ C
(iii) A ⊄ B
(iv) C ⊂ D
(v) B ⊂ D
Sol: (i) A ∩ D = A
∴ A ⊂ D
∴ given statement is true,
(ii) False, since every element of C is an element of B
∴ C ⊂ B
(iii) True, clearly every member of A is not a member of B,
(iv) True, Clearly from figure, every element of set C is a member of set D.
(v) True, Clearly from figure, every element of set B is a member of set D.
–: End Sets Class 11 OP Malhotra Exe-1C ISC Maths Ch-1 Latest editions :–
Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions
Thanks
Please share with your friends


