Sets Class 11 OP Malhotra Exe-1E ISC Maths Solutions Ch-1 Latest editions. In this article you would learn about Intersection of Sets and its properties. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.
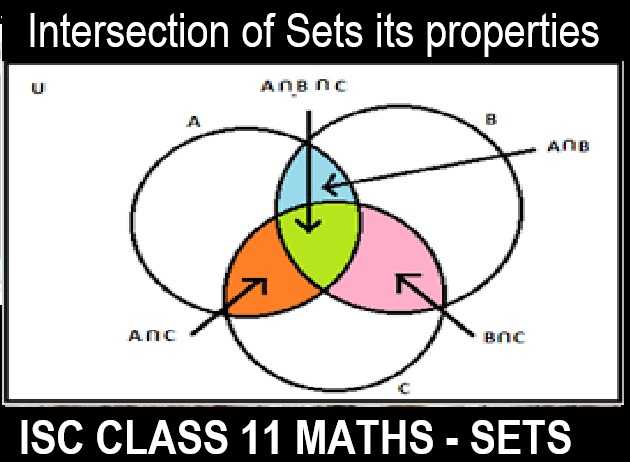
Sets Class 11 OP Malhotra Exe-1E ISC Maths Solutions Ch-1
| Board | ISC |
| Publications | S Chand |
| Subject | Maths |
| Class | 11th |
| Chapter-1 | Sets |
| Writer | OP Malhotra |
| Exe-1(E) | Intersection of Sets and its properties |
Exercise- 1E
Sets Class 11 OP Malhotra Exe-1E ISC Maths Solutions Ch-1 Latest editions.
Que-1: Find A∩B if :
(i) A = {1, 2, 3} and B = {1, 3, 5}
(ii) A = {a, e, i, o, u} and B = {a, r, e}
(iii) A = {letters in the word ‘nation’} and B = {t, r, a, i, n}
Sol: (i) A = {1, 2, 3} and B = {1, 3, 5}
A∩B = {1, 2, 3} ∩ {1, 3, 5}
= {1, 3}
(ii) A = {a, e, i, o, u} and B = {a, r, e}
A∩B = {a, e, i, o, u} ∩ {a, r, e}
= {a, e}
(iii) A = {letters in the word ‘nation’} and B = {t, r, a, i, n}
A∩B = {n, a, t, i, o} ∩ {t, r, a, i, n}
= {n, a, t, i}.
Que-2: (i) A = {x : x ∈ N and x is a multiple of 3}
B = {x : x ∈ N and x < 10}.
(ii) A = {x : x ∈ N and 1< x ≤ 6}
B = {x : x ∈ N and 6 < x < 10}
(iii) A = {1, 2, 3} and B = Φ
Sol: (i) A = {x : x ∈ N and x is a multiple of 3}
B = {x : x ∈ N and x < 10}.
A∩B = {3, 6, 9, 12, 15…} ∩ {1, 2, 3, 4, 5, 6, 7, 8, 9}
= {3, 6, 9}.
(ii) A = {x : x ∈ N and 1< x ≤ 6}
B = {x : x ∈ N and 6 < x < 10}
A∩B = {2, 3, 4, 5, 6} ∩ {7, 8, 9}
= {Φ}.
(iii) A = {1, 2, 3} and B = Φ
A∩B = {1, 2, 3} ∩ {Φ}
= {Φ}.
Que-3: If A = {5, 6, 7, 8, 9}, B = {10, 11, 12}, C = {6, 7, 11, 12, 13}, D = {5, 12, 13, 15}, find :
(i) A∩C (ii) A∩D (iii) B∩C (iv) B∩D (v) A∩B (vi) (A∩B)∩C (vii) (B∩C)∪(A∩B) (viii) (A∩D)∩(B∩C).
Sol: Given that :
A = {5, 6, 7, 8, 9}, B = {10, 11, 12}, C = {6, 7, 11, 12, 13}, D = {5, 12, 13, 15}
(i) A∩C = {5, 6, 7, 8, 9} ∩ {6, 7, 11, 12, 13}
= {6, 7}
(ii) A∩D = {5, 6, 7, 8, 9} ∩ {5, 12, 13, 15}
= {5}
(iii) B∩C = {10, 11, 12} ∩ {6, 7, 11, 12, 13}
= {11, 12}
(iv) B∩D = {10, 11, 12} ∩ {5, 12, 13, 15}
= {12}
(v) A∩B = {5, 6, 7, 8, 9} ∩ {10, 11, 12}
= {Φ}
(vi) (A∩B)∩C
A∩B = {5, 6, 7, 8, 9} ∩ {10, 11, 12}
= {Φ}
(A∩B)∩C = {Φ} ∩ {6, 7, 11, 12, 13}
= {Φ}
(vii) (B∩C)∪(A∩B)
B∩C = {10, 11, 12} ∩ {6, 7, 11, 12, 13}
= {11, 12}
A∩B = {5, 6, 7, 8, 9} ∩ {10, 11, 12}
= {Φ}
(B∩C)∪(A∩B) = {11, 12} ∪ {Φ}
= {11, 12}.
(viii) (A∩D)∩(B∩C)
A∩D = {5, 6, 7, 8, 9} ∩ {5, 12, 13, 15}
= {5}
B∩C = {10, 11, 12} ∩ {6, 7, 11, 12, 13}
= {11, 12}
(A∩D)∩(B∩C) = {5} ∩ {11, 12}
= {Φ}.
Que-4: If A = {2, 4, 6, 8, 10, 12}, B = {1, 6, 7, 10, 11, 12}, C = {2, 5, 8, 12, 15}, prove that
(i) A∩B = B∩A (ii) (A∩B)∩C = A∩(B∩C)
Sol: Given that :
A = {2, 4, 6, 8, 10, 12}
B = {1, 6, 7, 10, 11, 12}
C = {2, 5, 8, 12, 15}
(i) A∩B = {6, 10, 12}
B∩A = {6, 10, 12}
hence A∩B = B∩A
(ii) A∩B = {6, 10, 12}
(A∩B)∩C = {12}
B∩C = {12}
A∩(B∩C) = {12}
hence, (A∩B)∩C = A∩(B∩C).
Que-5: If A = {x : x is a natural number}, B = {x : x is an even natural number}, C = {x : x is an odd natural number} and D = {x : x is a prime number}, find :
(i) A∩B (ii) A∩C (iii) A∩D (iv) B∩C (v) B∩D (vi) C∩D
Sol: According to the question,
A = {1, 2, 3, 4, 5, 6, 7, . . . . . . . .}
B = {2, 4, 6, 8, 10, 12, . . . . . . . .}
C = {1, 3, 5, 7, 9, 11, 13, . . . . . . . }
D = {2, 3, 5, 7, 11, 13, . . . . . . . . .}
Therefore,
(i) A ∩ B = {2, 4, 6, 8, 10, 12, . . . . . . . .} = B
(ii) A ∩ C = {1, 3, 5, 7, 9, 11, 13, . . . . . . . } = C
(iii) A ∩ D = {2, 3, 5, 7, 11, 13, . . . . . . . . .} = D
(iv) B ∩ C = ∅
As there is no natural number which is odd as well as even, therefore,
B ∩ C = ∅
(v) B ∩ D = {2}
As the only prime number which is even is 2, therefore, B ∩ D = {2}
(vi) C ∩ D = {3, 5, 7, 11, 13} = D – {2}
Every odd prime number lies in this set.
As D is the set of prime numbers, therefore, C ∩ D will be the set D excluding the element 2.
=> C ∩ D = D – {2}
Que-6: Which of the following pairs of sets are disjoints ?
(i) {1, 2, 3, 4} and {x : x is a natural number 4 ≤ x ≤ 6}
(ii) {a, e, i, o, u} and {c, d, e, f}
(iii) {x : x is an even number} and {x : x is an odd number}
(iv) {x : x is a prime number} and {x : x is an even natural number}
Sol: (i) The first set is {1, 2, 3, 4}
The second set is {x : x is a natural number and 4 ≤ x ≤ 6}
= {4, 5, 6}
Now,
{1, 2, 3, 4} ∩ {4, 5, 6} = {4} ≠ Φ
Therefore, this pair of sets is NOT disjoint.
(ii) {a, e, i, o, u} ∩ {c, d, e, f} = {e} ≠ Φ
Therefore, this pair of sets are NOT disjoint.
(iii) {x : x is an even integer} ∩ {x : x is an odd integer} = Φ because there is no integer which can be both even and odd.
Therefore, this pair of sets is disjoint
(iv) {x : x is a prime number} ∩ {x : x is an even natural number} = {2} because there is integer which can be both prime and even natural.
Therefore, this pair of sets is not disjoint.
Que-7: Let A = {x : 2x+9=0, x ∈ N}, B = {1, 2, 3, 4}, find out whether A and B are disjoints sets or not.
Sol: Yes this is disjoints sets because
2x+9 = 0
x = 9/2
which is ∉ N
so, A = Φ
∴ A ∩ B = Φ.
Que-8: In the given Venn diagram, shade the region A∪(B∩C).
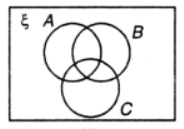
Sol: A∪(B∩C).

Que-9: If A and B are two sets, then A∩(A∪B) is equal to
(a) A (b) B (c) Φ (d) A∩B
Sol: (a) A
Given that: A ∩ (A ∪ B)
Let x ∈ A ∩ (A ∪ B)
⇒ x ∈ A and x ∈ (A ∪ B)
⇒ x ∈ A and (x ∈ A or x ∈ B)
⇒ (x ∈ A and x ∈ A) or (x ∈ A and x ∈ B)
⇒ x ∈ A or x ∈ (A ∩ B)
⇒ x ∈ A.
Que-10: If sets A and B are defined as :
A = {(x,y) | y = 1/x, 0 ≠ x ∈ R}, B = {(x,y) | y = -x, x ∈ R}. Then
(a) A∩B = A (b) A∩B = B (c) A∩B = Φ (d) A∪B = B
Sol: (c) A∩B = Φ
Given that, A = R{(x,y) ∣ y = 1/x, 0 ≠ x ∈ R}
And = {(x, y) | y = – x, x ∈ R}
It is very clear that y = 1/x and y = – x
∵ 1/x ≠ -x
∴ A ∩ B = Φ
–: End Sets Class 11 OP Malhotra Exe-1E ISC Maths Ch-1 Latest editions :–
Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions
Thanks
Please share with your friends


