Sets Class 11 OP Malhotra Exe-1F ISC Maths Solutions Ch-1 Latest editions. In this article you would learn about Difference of Sets. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.
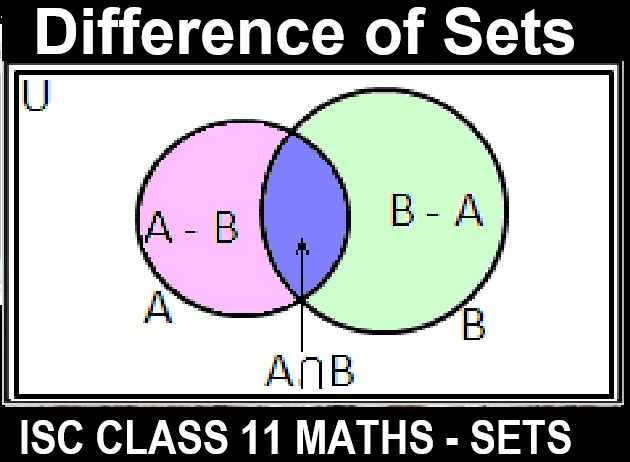
Sets Class 11 OP Malhotra Exe-1F ISC Maths Solutions Ch-1 Latest editions
| Board | ISC |
| Publications | S Chand |
| Subject | Maths |
| Class | 11th |
| Chapter-1 | Sets |
| Writer | OP Malhotra |
| Exe-1(F) | Difference of Sets |
Exercise- 1F
Sets Class 11 OP Malhotra Exe-1F ISC Maths Solutions Ch-1 Latest editions.
Que-1: If X = {a, b, c, d} and Y = {f, b, d, g}, find :
(i) X-Y (ii) Y-X
Sol: The given sets are:
X= { a, b, c, d } and Y = { f, b, d, g}.
The difference between two sets A and B is a set denoted by A-B and is obtained by writing the elements of A that are NOT in B in a set.
(i) X – Y = {a, c}
(ii) Y – X = { f , g}
Que-2: If A = {3, 6}, B = {3, 6, 9, 12}, then find
(i) A-B (ii) B-A
Sol: The given sets are :
A = {3, 6}, B = {3, 6, 9, 12}
The difference between two sets A and B is a set denoted by A-B and is obtained by writing the elements of A that are NOT in B in a set.
(i) A – B = {Φ}
because A⊂B.
(ii) B – A = {9, 12}
Que-3: If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8}, find.
(i) A-B (ii) B-C (iii) A-C (iv) C-A
Sol: Given sets are :
A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8}
The difference between two sets A and B is a set denoted by A-B and is obtained by writing the elements of A that are NOT in B in a set.
(i) A-B = {1, 2}
(ii) B-C = {3, 4}
(iii) A-C = {1, 2, 3, 4}
(iv) C-A = {5, 6, 7, 8}
Que-4: If A = {1, 2, 3, 4, 5, 6} and B = {2, 4, 6, 8}, show that A-B ≠ B-A
Sol: Given sets are :
A = {1, 2, 3, 4, 5, 6} and B = {2, 4, 6, 8}
The difference between two sets A and B is a set denoted by A-B and is obtained by writing the elements of A that are NOT in B in a set.
Taking L.H.S
A-B = {1, 3, 5}
Taking R.H.S
B-A = {8}
L.H.S is not equal to R.H.S
A-B ≠ B-A
Hence proved.
Que-5: If R is the set of real number and Q the set of rational numbers, then what is R – Q?
Sol: It is given that
R: a set of real numbers
Q: a set of rational numbers
The difference between two sets A and B is a set denoted by A-B and is obtained by writing the elements of A that are NOT in B in a set.
Therefore,
R – Q is a set consisting of real numbers that are NOT rational.
i.e., R – Q is a set of irrational numbers.
Que-6: If L = {1, 2, 3, 4}, M = {3, 4, 5, 6} and N = {1, 3, 5}, then verify that L – (M∪N) = (L-M)∩(L-N).
Sol: M = {3, 4, 5, 6}, N = {1, 3, 5}
⇒ M ∪ N = {1, 3, 4, 5, 6}
L = {1, 2, 3, 4} and M ∪ N = {1, 3, 4, 5, 6}
⇒ L – (M ∪ N) = {2} ……(1)
L = {1, 2, 3, 4} and M = {3, 4, 5, 6}
⇒ L – M = {1, 2}
L = {1, 2, 3, 4} and N = {1, 3, 5}
⇒ L – N = {2, 4}
L – M = {1, 2} and L – N = {2, 4}
⇒ (L – M) ∩ (L – N) = {2} …….(2)
Clearly, from (1) and (2)
L – (M ∪ N) = (L – M) ∩ (L – N)
Hence verified
Que-7: With the help of Venn diagram, show that for all sets A, B and C.
(i) (A-B)∪(A∩B) = A (ii) (A∪B)-B = A-B (iii) A-(B-C) ≠ (A-B)-C
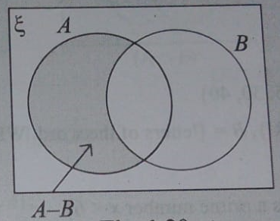
Sol: (i) It is clear from the Venn diagram.
(A-B)∪(A∩B) = A

(ii) It is clear from the Venn diagram that if B is taken out from (A∪B) then, A-B is left.
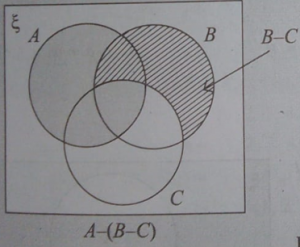
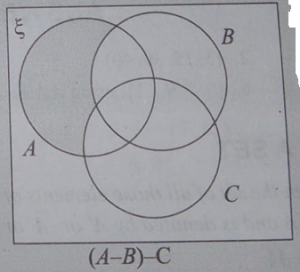
(iii) Clearly, A-(B-C) ≠ (A-B)-C
A-(B-C)
(A-B)-C.
–: End Sets Class 11 OP Malhotra Exe-1D ISC Maths Ch-1 Latest editions :–
Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions
Thanks
Please share with your friends


