Sets Class 11 OP Malhotra Exe-1H ISC Maths Solutions Ch-1 Latest editions. In this article you would learn about Complement of Sets and its Laws. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.
Sets Class 11 OP Malhotra Exe-1H ISC Maths Solutions Ch-1
| Board | ISC |
| Publications | S Chand |
| Subject | Maths |
| Class | 11th |
| Chapter-1 | Sets |
| Writer | OP Malhotra |
| Exe-1(H) | Complement of Sets and its Laws. |
Exercise- 1H
Sets Class 11 OP Malhotra Exe-1H ISC Maths Solutions Ch-1 Latest editions.
Que-1: If ξ = {a, b, c, d, e, f, g, h}, find the complement of the following sets :
(i) A = {a, b, c} (ii) B = {d, e, f, g} (iii) C = {a, c, e, g} (iv) D = {f, g, h, a}
Sol: The universal set is,
U = { a, b, c, d, e, f, g, h}.
The complement of a set A is U-A
where U is Universal set.
Thus,
(i) A’ = U – A = { a, b, c, d, e, f, g, h} – {a, b, c} = {d , e, f , g, h}
(ii) B’ = U – B = { a, b, c, d, e, f, g, h} – {d, e, f, g} = {a, b, c, h}
(iii) C’ = U – C = { a, b, c, d, e, f, g, h} – {a, c, e, g} = {b, d , f, h}
(iv) D = U – D = { a, b, c, d, e, f, g, h} – {f, g, h, a} = {b, c, d, e}
Que-2: If ξ = {1, 2, 3, 4}, A = {1, 4}, B = {1, 3}, then list the elements of
(i) A’ (ii) B’ (iii) (A∩B)’ (iv) (A∪B)’ (v) A’∩B’ (vi) A’∪B’
also show that (A∩B)’ = A’∪B’ and (A∪B)’ = A’∩B’.
Sol: Given sets are :
ξ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 3, 6, 10}
B = {1, 3, 5, 7, 9}
C = {1, 4, 9}
(i) A’ = ξ – A
= {2, 3}
(ii) B’ = ξ – B
= {2, 4}
(iii) {A∩B}’
{A∩B} = {1}
{A∩B}’ = ξ – {1}
= {2, 3, 4}
(iv) {A∪B}’
{A∪B} = {1, 3, 4}
{A∪B}’ = ξ – {1, 3, 4}
= {2}.
(v) A’∩B’
A’ = {2, 3}
B’ = {2, 4}
A’∩B’ = {2}
(vi) A’∪B’
= {2, 3}∪{2, 4}
= {2, 3, 4}.
show that (A∩B)’ = A’∪B’
A’ = {2, 3}
B’ = {2, 4}
Taking LHS
(A∩B) = {1}
(A∩B)’ = ξ – {1}
= {2, 3, 4}
Taking RHS
A’∪B’
{2, 3}∪{2, 4}
= {2, 3, 4}
LHS = RHS
(A∩B)’ = A’∪B’ Hence Proved.
Show that (A∪B)’ = A’∩B’
Taking LHS
(A∪B) = {1, 3, 4}
(A∪B)’ = ξ – {1, 3, 4}
= {2}
Taking RHS
A’∩B’
= {2, 3}∩{2, 4}
= {2}
LHS = RHS
(A∪B)’ = A’∩B’
Hence Proved.
Que-3: ξ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {1, 3, 6, 10}, B = {1, 3, 5, 7, 9}, C = {1, 4, 9}, then lists the elements of the following sets.
(i) (A-B)’ (ii) (C-B)’ (iii) (C-A)’ (iv) (A∪B)’ (v) (A∩B)’ (vi) (A’∩B)∩C’
(vii) (B’∪C)∩A’ (viii) (A∪B∪C)’ (ix) (A∩B∩C)’
Sol: ξ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 3, 6, 10}
B = {1, 3, 5, 7, 9}
C = {1, 4, 9}
(i) (A-B)’
(A-B) = {6, 10}
(A-B)’ = ξ – {6, 10}
= {1, 2, 3, 4, 5, 7, 8, 9}
(ii) (C-B)’
(C-B) = {4}
(C-B)’ = ξ – {4}
= {1, 2, 3, 5, 6, 7, 8, 9, 10}
(iii) (C-A)’
(C-A) = {4, 9}
(C-A)’ = ξ – {4, 9}
= {1, 2, 3, 5, 6, 7, 8, 10}
(iv) (A∪B)’
(A∪B) = {1, 3, 5, 6, 7, 9, 10}
(A∪B)’ = ξ – {1, 3, 5, 6, 7, 9, 10}
= {2, 4, 8}
(v) (A∩B)’
(A∩B) = {1, 3}
(A∩B)’ = ξ – {1, 3}
= {2 4, 5, 6, 7, 8, 9, 10}
(vi) (A’∩B)∩C’
A’ = ξ – A
= {2, 4, 5, 7, 8, 9}
B = {1, 3, 5, 7, 9}
(A’∩B) = {5, 7, 9}
C’ = ξ – C
= {2, 3, 5, 6, 7, 8, 10}
(A’∩B)∩C’ = {5, 7, 9}∩{2, 3, 5, 6, 7, 8, 10}
= {5, 7}
(vii) (B’∪C)∩A’
B’ = ξ – B
= {2, 4, 6, 8, 10}
C = {1, 4, 9}
(B’∪C) = {1, 2, 4, 6, 8, 9, 10}
A’ = {2, 4, 5, 7, 8, 9}
(B’∪C)∩A’ = {1, 2, 4, 6, 8, 9, 10} ∩ {2, 4, 5, 7, 8, 9}
= {2, 4, 8, 9}
(viii) (A∪B∪C)’
(A∪B∪C) = {1, 3, 4, 5, 6, 7, 9, 10}
(A∪B∪C)’ = ξ – {1, 3, 4, 5, 6, 7, 9, 10}
= {2, 8}
(ix) (A∩B∩C)’
(A∩B∩C) = {1}
(A∩B∩C)’ = ξ – {1}
= {2, 3, 4, 5, 6, 7, 8, 9, 10}.
Que-4: Taking the sets of natural numbers as the universal sets, write down the complements of the following sets:
(i) {x : x is an even natural number} (ii) {x : x is a positive multiple of 3}
(iii) {x : x is a prime number} (iv) {x : x is a natural number divisible by 3 and 5}
(v) {x : x + 5 = 8} (vi) {x : 2x + 5 = 9} (vii) {x : x ≥ 7} (viii) {x : x∈N and 2x+1 > 10}
Sol: (i) {x : x is an even natural number}
Even natural number = {2, 4, 6, 8, 10, ……..}
Complements = odd natural number
= {1, 3, 5, 7, 9, ……}
(ii) {x : x is a positive multiple of 3}
Multiple of 3 = {3, 6, 9, 12, …..}
Complement = Natural number not divisible by 3
= {1, 2, 4, 5, 7,……}
(iii) {x : x is a prime number}
Prime number = {2, 3, 5, 7, 11, 13, ….}
Complement = Natural number that are not prime number
= {1, 4, 6, 8, 9, 10, 12, 14, …..}
(iv) {x : x is a natural number divisible by 3 and 5}
Number divisible by both 3 and 5 = Multiple of 15 = {15, 30, 45, 60,….}
Complement = Natural number not divisible by 15
= {1, 2, 3, ……, 14, 16, 17, ….}
(v) {x : x + 5 = 8}
x + 5 = 8
x = 3
Complement = Number without 3
= {1, 2, 4, 5, 6, 7, …..}
(vi) {x : 2x + 5 = 9}
2x + 5 = 9
2x = 4
x = 2
Complement = Number without 2
= {1, 3, 4, 5, 6, 7,……}
(vii) {x : x ≥ 7}
Set = {7, 8, 9, 10, …..}
Complement = Natural number less than 7
= {1, 2, 3, 4, 5, 6}.
(viii) {x : x∈N and 2x+1 > 10}
2x + 1 > 10
2x > 9
x > 4.5
x ≥ 5
Set = {5, 6, 7, 8, …..}
Complement = Number less than 5
= {1, 2, 3, 4}
Que-5: Let U be the set of all triangles in a plane. If A is the set of all triangles with at least one angle different from 60°, what is A’ ?
Sol: It is given that U is the set of all triangles in a plane.
Also, A is the set of all triangles with at least one angle different from 60°.
Then A’, which is the complement of A, is
A’ = U – A
= {All triangles} – {all triangles with at least one angle different from 60°}
= {All triangles in which all angles are equal to 60°}
= All equilateral triangles
Thus, A′ is the set of all equilateral triangles.
Que-6: Shade the region as directed :
(i) Complement of set B

(ii) (A∪B)’

(iii) A’∩C’
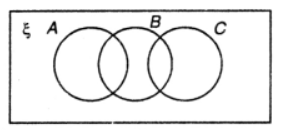
Sol: (i)
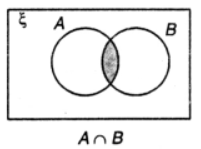
(ii)
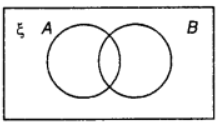
(iii)

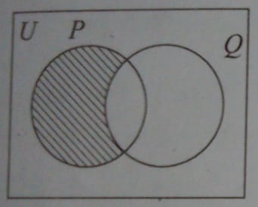
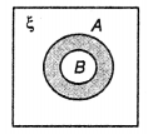
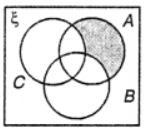
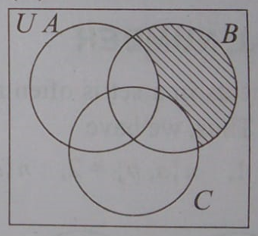
Que-7: Describe the shaded regions in the following diagrams.
(i)
(ii)
(iii)

(iv)
(v)

(vi)
Sol: (i) P∩Q’
(ii) A∩B’
(iii) (A∪B∪C)’
(iv) A∩B’∩C’
(v) B∩C∩A’
(vi) A’∩B∩C’
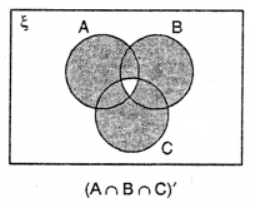
Que-8: Use the given diagram to shade the region (A∩B∩C)’.
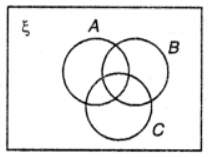
Sol: (A∩B∩C)’
–: End Sets Class 11 OP Malhotra Exe-1H ISC Maths Ch-1 Solutions :–
Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions
Thanks
Please share with your friends


