Sets Class 11 OP Malhotra Exe-1I ISC Maths Solutions Ch-1 Latest editions. In this article you would learn about Cardinal Number. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Sets Class 11 OP Malhotra Exe-1I ISC Maths Solutions Ch-1
| Board | ISC |
| Publications | S Chand |
| Subject | Maths |
| Class | 11th |
| Chapter-1 | Sets |
| Writer | OP Malhotra |
| Exe-1(I) | Cardinal Number. |
Exercise- 1I
Sets Class 11 OP Malhotra Exe-1I ISC Maths Solutions Ch-1 Latest editions.
Que-1: In n(ξ) = 80, n(A) = 48, n(B) = 40 and n(A∩B) = 25, draw a Venn diagram to find :
(i) n(A∪B) (ii) n(A∪B)’ (iii) n(A-B) (iv) n(B-A) (v) (A∩B)’ (vi) n(A’∩B)
Sol: Given :
n(ξ) = 80
n(A) = 48
n(B) = 40
n(A∩B) = 25
(i) n(AUB) = n(A) + n(B) – n(A n B)
= 48 + 40 – 25
= 63
(ii) n(AUB)’ = n(ξ) – n(AUB)
= 80 – 63
= 17
(iii) n(A-B) = n(A) – n(A∩B)
= 48 – 25
= 13
(iv) n(B-A) = n(B) – n(A∩B)
= 40 – 25
= 15.
(v) n(A∩B)’ = n(A) – n(A∩B)
= 48 – 25
= 23.
(vi) n(A’∩B) = n(B) – n(A)
= 40 – 25
= 15.
Que-2: If U = {x | x ∈ N, x < 10}, A = {x | x is a prime number, x < 10}, B = {x | x is an even number, x < 10} draw a Venn diagram to find :
(i) n(A∪B) (ii) n(A∩B) (iii) n(A∪B)’ (iv) n(A∩B’) (v) n(A’∩B)
Sol: Given :
U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {2, 3, 5, 7}
B = {2, 4, 6, 8}
(i) n(A∪B)
= {2, 3, 4, 5, 6, 7, 8}
= 7.
(ii) n(A∩B)
= {2}
= 1.
(iii) n(A∪B)’
= U – (A∪B)
= {1, 9}
= 2.
(iv) n(A∩B’)
= {3, 5, 7}
= 3.
(v) n(A’∩B)
= {4, 6, 8}
= 3.
Que-3: Given n(U) = 40, n(A’) = 12, n(B) = 15 and B⊂A. Draw a Venn diagram to illustrate this information. Hence find n(A-B).
Sol: Given n (ξ) = 40 ; n (A’) = 12 ; n (B) = 15 Also B ⊂ A
∴ (A – B) = 13
since n (A’) =12 ⇒ n (ξ) – n (A) = 12
n (A) = 40 – 12 = 28
∴ (A – B) = n (A) – n(A∩B)
= n (A) – n (B)
= 28 – 15 = 13
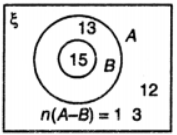
Que-4: The Venn diagram shows :
ξ = {pupils in class 8}, A = {pupils who play cricket}, B = {pupils who play basketball} How many pupils :

(i) are in class 8? (ii) play cricket? (iii) play basketball? (iv) play both cricket and basketball (v) play neither cricket nor basketball?
Sol: ξ = {pupils in class 8}
(i) number of pupils who are in class 8 = n(ξ) = 15 + 8 + 9 + 13 = 45
(ii) No. of pupils who play cricket = n(A) = 15 + 8 = 23
(iii) No. of pupils who play basketball = n (B) = 8 + 9 = 17
(iv) No. of pupils who play both cricket and basketball = n(A∩B) = 8
(v) No. of pupils who play neither cricket nor basketball = n (A’ ∩ B’) = n(A ∪ B)’
= n(ξ) – n(A∪B)
= 45 – (15 + 8 + 9) = 13
Que-5: In the Venn diagram:
ξ = {people at function}, A = {those who asked for tea}, B = {those who watched the ballet} :
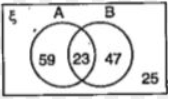
Write down the number who :
(i) asked for tea (ii) ask for tea and watched the ballet (iii) neither asked for tea nor watched the ballet (iv) attended the function.
Sol: (i) Required no. of peoples who asked for tea = n( A) = 59 + 23 = 82
(ii) Required no. of peoples who asked for tea and watched the ballet = n (A ∩ B) = 23
(iii) Required no. of peoples who neither asked for tea nor watched the ballet
= n( A’ ∩ B’) = n(A∪ B)’
= n(ξ) – n (A ∪ B) = 25
(iv) Required no. of peoples who attended the function = 59 + 23 + 47 + 25 = 154
Que-6: If X and Y are two sets such that X∪Y has 18 elements, X has 8 elements and Y has 15 elements, how many elements does X∩Y have ?
Sol: It is given that X and Y are two sets such that
n (X) = 8, n (Y) = 15 and n (X υ Y) = 18
We know that n(X ∪ Y) is,
n (X ∪ Y) = n (X) + n (Y) – n (X ∩ Y)
n (X ∩ Y) = n (X) + n (Y) – n (X ∪ Y)
= 8 + 15 – 18
= 23 – 18
= 5
Therefore, n ( X ∩ Y ) = 5.
Que-7: If S and T are two sets such that S has 21 elements, T has 32 elements and S∩T has 11 elements, how many elements does S∪T have ?
Sol: It is given that S and T are two sets such that:
n (S) = 21, n (T) = 32 and n (S ∩ T) = 11
We know that n(S ∪ T) is,
n (S ∪ T) = n (S) + n (T) – n (S ∩ T)
= 21 + 32 – 11
= 53 – 11
= 42
Therefore, S ∪ T has 42 elements.
Que-8: If X and Y are two sets such that X has 40 elements, X∪Y has 60 elements and X∩Y has 10 elements, how many elements does Y have ?
Sol: It is given that X and Y are two sets such that:
n (X) = 40, n (X ∪ Y) = 60 and n (X ∩ Y) = 10
We know that n(X υ Y) is,
n (X ∪ Y) = n (X) + n (Y) – n (X ∩ Y)
From this,
n (Y) = n (X ∩ Y) + n (X ∪ Y) – n (X)
= 10 + 60 – 40
= 70 – 40
= 30
Therefore, n (Y) = 30
Thus, the set Y has 30 elements
–: End Sets Class 11 OP Malhotra Exe-1I ISC Maths Ch-1 Solutions :–
Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions
Thanks
Please share with your friends


