Sets Class 11 OP Malhotra Exe-1J ISC Maths Solutions Ch-1 Solutions. In this article you would learn about Practical Problems. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Sets Class 11 OP Malhotra Exe-1J ISC Maths Solutions Ch-1
| Board | ISC |
| Publications | S Chand |
| Subject | Maths |
| Class | 11th |
| Chapter-1 | Sets |
| Writer | OP Malhotra |
| Exe-1(J) | Practical Problems. |
Exercise- 1J
Sets Class 11 OP Malhotra Exe-1J ISC Maths Solutions Ch-1 Solutions
Que-1: In a class of 35 students, 24 like to play cricket and 16 like to play football. Also each student likes to play at least one of two games. How many students like to play both cricket and football ?
Sol: Total number of students = 35
Students who like cricket (C) = 24
Students who like football (F) = 16
Every student likes at least one of the two games.
Total = C∪F = C + F − C∩F
35 = 24 + 16 − C∩F
35 = 40 − C∩F
C∩F = 40−35 = 5
Que-2: In a group of 70 people, 37 like coffee, 52 like tea and each person like at least one of two drinks. How many people like both coffee and tea ?
Sol: Let C denote the set of people who like coffee, and T denote the set of people who like tea.
It is given that in a group of 70 people, 37 like coffee, 52 like tea and each person likes at least one of the two drinks.
Therefore,
n (C) = 37, n (T) = 52 and n (C υ T) = 70.
We know that n(C υ T) is given by,
n (C υ T) = n (C) + n (T) – n (C ∩ T)
From this,
n (C ∩ T) = n (C) + n (T ) – n (C υ T)
= 37 + 52 – 70
= 89 – 70
= 19
Therefore, 19 people like both coffee and tea.
Que-3: In a group of students, 100 students know Hindi; 50 know English and 25 know both. Each of the students know either Hindi or English. How many students are there in a group ?
Sol: Let U be the set of all students in the group.
E be the set of all students who know English.
H be the set of all students who know Hindi.
It is given that
n (H) = 100, n (E) = 50, n (H ∩ E) = 25
We know that
n (H υ E) = n (H) + n (E) – n (H ∩ E)
= 100 + 50 – 25
= 150 – 25
= 125
Hence, there are 125 students in the group.
Que-4: In a survey of 400 students in a school, 100 were listed as taking apple juice, 150 as taking orange juice and 75 were listed as taking both apple as well as orange juice. Find how many students were taking neither apple juice nor orange juice.
Sol: Let X = Total number of students in class, A = Number of students who liked apple juice and O = Number of students who liked orange juice.
Given: n (X) = 400, n (A) = 100, n (O) = 150 and n (A ∩ O) = 75.
We have to find the number of students who study neither liked apple nor orange juice.
i.e n (A ∪ O)’.
⇒ n (A ∪ O) = n (A) + n (O) – n (A ∩ O)
⇒ n (A ∪ O) = 100 + 150 – 75 = 175
We know that, n (A ∪ O)’
= n (X) – n (A ∪ O)
⇒ n (A ∪ O)’
= 400 – 175
= 225.
Que-5: In a college 500 students study Mathematics and 400 study Economics. If 200 students study both the subjects, find the total number of students enrolled in these two subjects.
Sol: Given : 500 student study maths,
400 study economy
200 student study both these subjects.
As we know, n( A ∪ B ) = n( A ) + n( B ) – n( A ∩ B )
Let’s consider X as total number of students in college.
Consider M and E as sets of maths and economy students.
∴ n( M ) = 500 and n( E ) = 400
Acc. to the question, 200 students study both maths and economy.
∴ n( M ∩ E ) = 200
The above mentioned 200 students have been counted twice in the enrolled list.
Now, the total students who enrolled will be
n( M ∪ E ) = n( M ) + n( E ) – n( M ∩ E )
= 500 + 400 – 200
= 900 – 200
= 700
Que-6: In a group of 70 people, 48 speak Tamil, 36 speak English and all the people speak at least one language find :
(i) How many speak both the languages? (ii) How many speak only Tamil?
(iii) How many speak only English?
Sol: Given :
Total number of people = 70
People who speak Tamil = 48
People who speak English = 36
Everyone speaks at least one language.
Let :
T = set of people who speak Tamil
E = set of people who speak English
T∪E = 70 (since everyone speaks at least one language)
∣T∣ = 48, |E| = 36
Let x be the number of people who speak both languages
∣T∪E∣ = ∣T∣ + ∣E∣ − ∣T∩E∣
70 = 48 + 36 − x
70 = 84−x
⇒ x = 14.
(i) How many speak both the languages?
= 14 people
(ii) How many speak only Tamil?
= 48−14 = 34 people
(iii) How many speak only English?
= 36−14 = 22 people
Que-7: Out of 100 candidates who appeared in an entrance test in English and Mathematics, 80 passed in at least one subject. If 60 passed in English and 65 in Mathematics, find :
(i) How many passed is both the subjects? (ii) How many passed in English only? (iii) How many failed in Mathematics?
Sol: Given :
Total candidates = 100
Candidates who passed at least one subject = 80
Passed in English = 60
Passed in Mathematics = 65
Let :
E = set of students who passed in English = 60
MMM = set of students who passed in Mathematics = 65
E∪M = 80 (since 80 passed in at least one subject)
Let x be the number of students who passed both subjects
∣E∪M∣ = ∣E∣ + ∣M∣ − ∣E∩M∣
80 = 60 + 65 − x
⇒ 80 = 125−x
⇒ x = 45
(i) How many passed in both subjects?
→ 45
(ii) How many passed in English only?
→ 60−45 =15
(iii) How many failed in Mathematics?
→ Total students = 100, passed in Math = 65
→ Failed in Math = 100−65 = 35
Que-8: In a group of 30 people, 18 play squash and 19 play tennis. How many play both games, provides everyone plays at least one game?
Sol: Let S = set of all peoples who play squash
T = set of all peoples who play Tennis
∴ n(S) = 18 ; n(T) = 19
Also given n (S ∪ T) = 30
∴ No. of peoples who play both games
= n(S∩T) = n(S) + n(T) – n(S∪T)
= 18 + 19 – 30 = 7
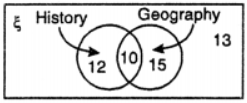
Que-9: In a class of 50 students, 22 like History, 25 like Geography and 10 like both subjects. Draw a Venn diagram and find the number of students who
(i) do not like History (ii) do not like Geography (iii) like neither History nor Geography
Sol: Let H = set of all students who like History
G = set of all students who like geography
and ξ = set of all students
Thus, n (ξ) = 50 ; n (H) = 22 ; n (G) = 25 and n (G ∩ H) = 10
(i) ∴ Required no. of students who do not like History
= n (H’) = n (ξ) – n (H)
= 50 – 22 = 28
(ii) Required no. of students who do not like Geography = 25
(iii) Required no. of students who like neither History nor Geography = n (H’ ∩ G’)
= n(H∪G)’ = n(ξ) – n(H∪G)
= 50 – 37 = 13
Que-10: 2000 candidates appear in a written test in Mathematics and General Awareness for a Government job. 1800 passed in at least one subject. If 1200 passed in Mathematics and 1500 in General Awareness find : (i) How many passed in both the subjects (ii) How many passed in Mathematics only (iii) How many failed in General Awareness?
Sol: Let M = set of all candidates who passed in Mathematics
G = set of all candidates who passed G.A test
Then n (M) = 1200 ; n (G) = 1500 and n(G∪M) = 1800
(i) Required no. of candidates who passed in both the subjects = n(M∩G)
= n (M) + n (G) – n (M ∪ G)
= 1200 + 1500 – 1800 = 900
(ii) ∴ Required no. of candidates who passed in Maths only = n (M ∩ G’)
= n (M) – n (M ∩ G)
= 1200 – 900 = 300
(iii) Required no. of candidates who failed in G.A = n (G’) = n(ξ) – n (G)
= 2000 – 1500 = 500
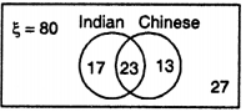
Que-11: In a group of 80 people, 40 like Indian food, 36 like Chinese food and 27 do not like any kind of these foods. Draw Venn diagram to find :
(i) How many like both kind of food? (ii) How many like only the Indian food? (iii) How many like only the Chinese food?
Sol: Let A = set of peoples who like Indian food
B = set of peoples who like Chinese food
Then n (A) = 40 ; n (B) = 36 and n (ξ) = 80
(i) Also, no. of peoples who donot like any kind of peoples
= n (A’ ∩ B’) = n(A ∪ B)’
27 = n(ξ) – n(A∪B)
⇒ n (A ∪ B) = 80 – 27 = 53
∴ n (A ∩ B) = n (A) + n(B) – n(A∪B)
= 40 + 36 – 53 = 23
(ii) No. of peoples who like only indian food
= n(A ∩ B’) = 17
(iii) No. of peoples who like only Chinese food
= n(A’ ∩ B) = 13
Que-12: In a group of people, two-seventh speak Bengali only and three-seventh speak Hindi only. If 20 people speak none of these languages and 80 speak both, find using Venn diagram the total number of people in the group.
Sol: Let the total number of peoples in the group be x.
∴ n(ξ) = x
Let B = set of all peoples who speak Bengali
and H = set of all peoples who speak Hindi
Then n (B ∩ H’) = 2/7; n (H ∩ B’) = 3/7x
given no. of peoples who speak none of these languages = 20
and Number of peoples who speak both these languages = 80

From Venn diagram, we have
(2x/7) + 80 + (3x/7) + 20 = x
⇒ (5x/7) + 100 = x
⇒ 100 = x – (5x/7) = (2x/7)
⇒ 2x = 700
⇒ x = 350
Hence, the required no. of peoples in the group be 350.
Que-13: A firm has 40 workers working in the factory premises, 30 working in its office and 20 working in both the places. How many workers are there in the firm? How many are working in the (i) factory (ii) office alone ?
Sol: Let F be the set of all workers working in factory premises and O be the set of all workers working in office
Then n (F) = 40 and n (O) = 30
and n (F ∩ O) = 20
Total no. of workers working in the firm = 20 + 20+ 10 = 50
(i) Total no. of workers working in factory alone = n(F ∩ O’) = 20
(ii) Total no. of workers working in office alone = n (O ∩ F’) = 10
Que-14: There are 200 individuals with a skin disorder; 120 had been exposed to the chemical C1, 50 to chemical C2, and 30 to both the chemicals C1 and C2. Find the number of individuals exposed to
(i) Chemical C1 but not chemical C2 (ii) Chemical C2 but not chemical C1 (iii) Chemical C1 or chemical C2
Sol: Given :
Total individuals = 200
Exposed to chemical C1 = 120
Exposed to chemical C2 = 50
Exposed to both C1 and C2 = 30
(i) Only C1 = ∣C1∣ − ∣C1∩C2∣
= 120−30 = 90
(ii) Only C2 = ∣C2∣ − ∣C1∩C2∣
= 50−30 = 20
(iii) ∣C1∪C2∣ = ∣C1∣ + ∣C2∣ − ∣C1∩C2∣
= 120 + 50 − 30
= 140
Que-15: Out of 500 cars owner investigated, 400 owned car A and 200 owned car B, 50 owned both A and B cars. Is this data correct ?
Sol: Let A be the set of people owned car A
Let B be the set of people owned car B
n(A) = 400, n(B) = 200, n(A ∩ B) = 50
n(A ∪ B) = 500 …(1)
n(A) + n(B) – n(A ∩ B)
= 400 + 200 – 50
= 600 – 50
= 550 …(2)
From (1) and (2) we get
n(A ∪ B) ≠ n(A) + n(B) – n(A ∩ B)
∴ The given data is not correct.
Que-16: A survey shows that 63% of the people watch a news channel where as 76% watch another channel. If x% of the people watch both channels, then (a) x = 35, (b) x = 63, (c) 39≤x≤63 (d) x = 39
Sol: (c) 39≤x≤63
Reason:
Given :
% of people who watch the first news channel = 63%
% who watch the second channel = 76%
Let x% be the people who watch both channels
Since we are dealing with percentages, total = 100%
People who watch at least one channel = 63+76−x
= 139−x
This value must be ≤ 100% because that’s the total population.
So,
139−x ≤ 100 ⇒ x ≥ 39
Also, x can’t be more than 63% because only 63% watch the first channel, and both-watchers are a subset of that.
So,
x ≤ 63
Hence,
39 ≤ x ≤ 63.
–: End Sets Class 11 OP Malhotra Exe-1J ISC Maths Ch-1 Solutions :–
Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions
Thanks
Please share with your friends


