Sets Class 11 OP Malhotra Exe-1L ISC Maths Solutions Ch-1 Solutions. In this article you would learn about Algebra of Sets and Problem Based on laws. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Sets Class 11 OP Malhotra Exe-1L ISC Maths Solutions Ch-1
| Board | ISC |
| Publications | S Chand |
| Subject | Maths |
| Class | 11th |
| Chapter-1 | Sets |
| Writer | OP Malhotra |
| Exe-1(L) | Algebra of Sets and Problem Based on laws. |
Exercise- 1L
Sets Class 11 OP Malhotra Exe-1L ISC Maths Solutions Ch-1 Solutions
Very Short Answer Type Questions :
Que-1: Tell whether the collection of ten most talented writers of India is a set or not.
Sol: The collection of ten most talented writers of India is not a well-defined collection because the criteria for determining a writer’s talent may vary from person to person.
Hence, this collection is not a set.
Que-2: Write the set A = {1, 4, 9, 16, 25,….} in set builder form.
Sol: {x : x = n², n ∈ N}
Que-3: Write the set {3, 9, 27, 81} in set builder form.
Sol: {x : x = 3^n, n ∈ N and 1 ≤ n ≤ 4}
Que-4: Write the set {x ∈ R : 1 ≤ x ≤ 2} in Roaster form.
Sol: {1, 2}
Que-5: Write the solution set of the equation x² + x – 2 = 0 in Roaster form.
Sol: We will solve this quadratic equation.
We have the equation, x2 + x – 2 = 0.
We have to factorise it to get the solution in roster form.
x2 + 2x – x – 2 = 0
x (x + 2) -1 (x + 2) = 0
(x + 2) (x – 1) = 0
So, x = -2 or x = 1
Thus, the solution set of the equation x2 + x – 2 = 0 in roster form is {1, -2}.
Que-6: Write all subsets of set A = {a, b, c}
Sol: A = {a, b, c}
Subset of A are Ø, {a}, {b}, {c}, {a, b}, {b, c}, {a, c}, {a, b, c}.
Que-7: Write all subsets of set A = {Φ, 1}
Sol: Set A = {Ø, 1}
Subsets = Ø, {Ø}, {1}, {Ø, 1}
Que-8: Write the number of subsets of a set having ‘n’ elements.
Sol: For each of the n elements, there are possibilities: either it is in the subset or it is not.
Therefore, the total number of subsets is 2×2×…×2(n times).
2^n.
Que-9: Write the power set of {1, 2}
Sol: A = {1, 2}
Subset = Ø, {1}, {2}, {1, 2}
P(A) = {Ø, {1}, {2}, {1, 2}}
Que-10: The number of elements in the power set of A = {a, b, c} is …..
Sol: A = {a, b, c}
The number of elements in the power set of a set with n elements is 2^n
Set A has 3 elements
n = 3
2³ = 8.
Que-11: When A = Φ. Then the number of elements in P(A) is …..
Sol: A = ϕ
⇒ n(A) = 0
P(A) is a power set and number of elements in power set is 2x where x is number of elements in set A
Therefore,
n[P(A)] = 20 = 1
Que-12: If A = the set of letters in the word ‘PEAR’ and B = the set of letters in the word ‘REAP’, is A = B ?
Sol: A = ‘PEAR’
B = ‘REAP’
Two sets are equal if and only if they have the same elements, regardless of order.
A = {P, E, A, R}
B = {R, E, A, P}
Both sets contain the same elements : P, E, A, R
Since both sets contain the same elements,
A = B.
Que-13: Are the two sets A and B equal, if A = {a, b, c, d} and B = {a, b, c, p}?
Sol: Two sets are equal if and only if they have the same elements, regardless of order.
A = {a, b, c, d}
B = {a, b, c, p}
Both sets contain the different elements.
Since both sets contain the different elements,
A ≠ B.
Que-14: A = {1, 2, 3, 4, 5}, B = {2, 4, 6, 8}, then find
(i) A-B (ii) A∪B (iii) n(A∩B)
Sol: A = {1, 2, 3, 4, 5}
B = {2, 4, 6, 8}
(i) A-B
= {1, 3, 5}
(ii) A∪B
= {1, 2, 3, 4, 5, 6, 8}
(iii) n(A∩B)
(A∩B) = {2, 4}
n(A∩B) = {2}
Que-15: If U = {x : x ∈ N and x ≤ 10} and A = {x : x is a composite number}; then find A’.
Sol: U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {4, 6, 8, 9, 10}
A’ = U – A
= {1, 2, 3, 5, 7}.
Que-16: Let A = {All prime number less than 10} and B = {All odd number less than 10}, find {A – (A∩B)}.
Sol: Here, A = {2, 3, 5, 7,} and B = {1, 3, 5, 7, 9}.
A ∩ B = {2, 3, 5, 7} ∩ {1, 3, 5, 7, 9} = {3, 5, 7}
A – (A ∩ B) = {2, 3, 5, 7} – { 3, 5, 7} = {2}
Que-17: If U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {1, 2, 3, 4}, B = {2, 4, 6, 8}, find (A-B)’.
Sol: U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {1, 2, 3, 4}
B = {2, 4, 6, 8}
A-B = {1, 3}
(A-B)’ = U – {A-B}
= U – {1, 3}
= {2, 4, 5, 6, 7, 8, 9}.
Que-18: From the adjoining diagram, determine the following sets :
(i) (A∪B)’ (ii) (A∩B)’
Sol: (i) (A∪B)’ = {1, 3, 9, 10}
(ii) (A∩B)’ = {1, 2, 3, 4, 6, 7, 8, 9, 10}
Que-19: In the adjoining Venn diagram, shade the following sets.
(i) A’∩(B∪C) (ii) A’∩(C-B)
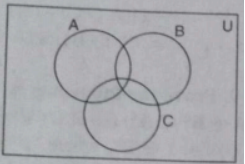
Sol:
–: End Sets Class 11 OP Malhotra Exe-1L ISC Maths Solutions Ch-1 Solutions. :–
Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions
Thanks
Please share with your friends


