Similarity Exercise Exe-15A Class-10 Concise ICSE Maths Solution Ch-15. In this article you would learn Criteria for Similarity of Two Triangle. We Provide Step by Step Solutions / Answer of questions for Selina Concise Maths. Visit official Website CISCE for detail information about ICSE Board Class-10 Mathematics.
If you have doubt such questions that What are the criteria for similarity of two triangles? What are three rules that prove two triangles are similar? What are the 5 ways to prove triangles similar? What are the four rules for similar triangles? Then this article is for you.

Similarity Exercise Exe-15A Class-10 Concise ICSE Maths Solution Ch-15
| Board | ICSE |
| Publications | Selina |
| Subject | Maths |
| Class | 10th |
| Chapter-15 | Similarity |
| Writer | R.K. Bansal |
| Exe-15A | Criteria for Similarity of Two Triangle |
| Edition | 2025-2026 |
Criteria for Similarity of Two Triangle
Similarity Exercise Exe-15A Class-10 Concise ICSE Maths Solution Ch-15
Que-1: In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that:
(i) ΔAPC and ΔBPD are similar.
(ii) If BD = 2.4 cm AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm; find the lengths of PA and PC.
Ans: (i) In ΔAPC and ΔBPD,
∠APC = ∠BPD …(Vertically opposite angles)
∠ACP = ∠BDP …(Alternate angles since AC || BD)
ΔAPC ∼ ΔBPD …(AA criterion for similarity)
(ii) In ΔAPC and ΔBPD,
∠APC = ∠BPD …(Vertically opposite angles)
∠ACP = ∠BDP …(Alternate angles since AC || BD)
∴ ΔAPC ∼ ΔBPD …(AA criterion for similarity)
So, PA/PB=PC/PD=AC/BD
=> PA/3.2=PC/4=3.6/2.4
So, PA/3.2=3.6/2.4 and PC/4=3.6/2.4
=> PA=3.6×3.2/2.4=4.8 cm
And PC = 3.6×4/2.4 = 6 cm
Hence, PA = 4.8 cm and PC = 6 cm
Que-2:In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that: (i) ΔAPB is similar to ΔCPD. (ii) PA x PD = PB x PC.
Ans: In trapezium ABCD AB || DC
Diagonals AC and BD intersect each other at P.
To prove:
(i) ΔAPB ~ ΔCPD.
(ii) PA x PD= PB x PC.
Proof: In ΔAPB and ΔCPD
∠APB = ∠CPD (Vertically opposite angles)
∠PAB = ∠PCD (Alternate angles)
ΔAPB ~ ΔCPD (AA axiom)
PA/PC = PB/PD
=> PA x PD = PB x PC
Hence proved.
Que-3: P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that: (i) DP : PL = DC : BL. (ii) DL : DP = AL : DC.
Ans: P is a point on side BC of a parallelogram ABCD.
DP is produced to meet AB produced at L.
To prove:
(i) DP : PL = DC : BL
(ii) DL : DP = AL : DC.
Proof:
(i) In ΔBPL and ΔCPD
∠BPL = ∠CPD (Vertically opposite angles)
∠PBL = ∠PCD (Alternate angles)
ΔBPL ~ ΔCPD (AA axiom)

Que-4: In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that: (i) ΔAOB is similar to ΔCOD. (ii) OA x OD = OB x OC.
Ans: Given : In quadrilateral ABCD, diagonals AC and BD intersect each other at O.
AO = 2CO, BO = 2DO.
To prove:
(i) ΔAOB is similar to ΔCOD.
(ii) OA x OD = OB x OC.

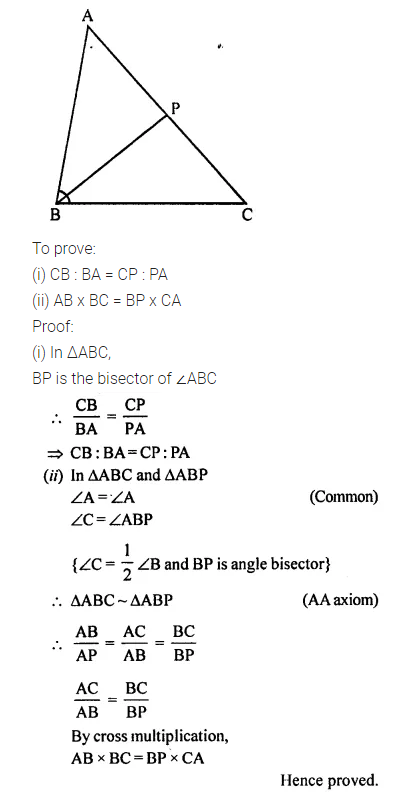
Que-5: In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that: (i) CB : BA = CP : PA (ii) AB x BC = BP x CA
Ans: In ΔABC,
∠ABC = 2∠ACB
Bisector of ∠ABC meets AC in P.
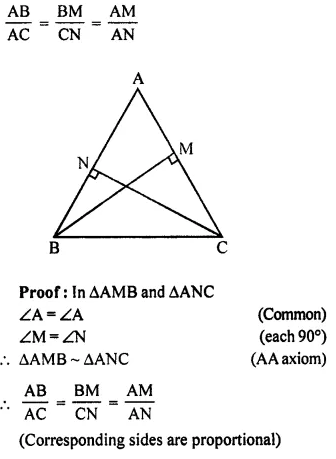
Que-6: In ΔABC; BM ⊥ AC and CN ⊥ AB; show that:
……………………
Ans: In ΔABC, BM ⊥ AC and CN ⊥ AB
To prove:
Que-7: In the given figure, DE // BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm. (i) Write all possible pairs of similar triangles. (ii) Find lengths of ME and DM.
Ans: In the given figure,
DE || BC
AE = 15 cm, EC = 9 cm NC = 6 cm and BN = 24 cm
(i) Write all the possible pairs of similar triangles.
(ii) Find lengths of ME and DM
Proof:
(i) In ΔABC
DE || BC
Pairs of similar triangles are
(a) ΔADE ~ ΔABC
(b) ΔADM ~ ΔABN
(c) ΔAME ~ ΔANC
(ii) ΔAME ~ ΔANC
and ΔADM ~ ΔABN

Que-8: In the given figure, AD = AE and AD² = BD x EC Prove that: triangles ABD and CAE are similar.
Ans: In the given figure,
AD = AE
AD² = BD x EC
To prove: ΔABD ~ ΔCAE
Proof: In ΔADC, AD = AE
∠ADE = ∠AED (Angles opposite to equal sides)
But ∠ADE + ∠ADB = ∠AED + ∠AEC = 180°
∠ADB = ∠AEC
AD² = BD x EC

Que-9: In the given figure, AB // DC, BO = 6 cm and DQ = 8 cm; find: BP x DO.
Ans: In the given figure, AB || DC,
BO = 6 cm, DQ = 8 cm
Find BP x DO
In ΔODQ and ΔOPB
∠DOQ = ∠POB (Vertically opposite angles)
∠DQO = ∠OPB (Alternate angles)

Que-10: Angle BAC of triangle ABC is obtuse and AB = AC. P is a point in BC such that PC = 12 cm. PQ and PR are perpendiculars to sides AB and AC respectively. If PQ = 15 cm and PR = 9 cm; find the length of PB.
Ans: In ΔABC, ∠ABC is an obtused angle,
AB =AC
P is a point on BC such that PC = 12 cm
PQ and PR are perpendiculars to the sides AB and AC respectively.
PQ = 15 cm and PR = 9 cm

Que-11: State, true or false :
(i) Two similar polygons are necessarily congruent
(ii) Two congruent polygons are necessarily similar.
(iii) All equiangular triangles are similar.
(iv) All isosceles triangles are similar.
(v) Two isosceles-right triangles are similar.
(vi) Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
(vii) The diagonals of a trapezium, divide each other into proportional segments.
Ans: (i) False,
(ii) True,
(iii) True,
(iv) False,
(v) True,
(vi) True,
(vii) True.
Que-12: Given………………..4x+2 find……………………..DE
Ans:

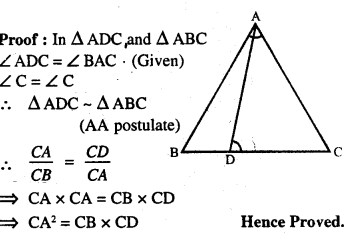
Que-13: D is a point on the side BC of triangle ABC such that angle ADC is equal to angle BAC. Prove that CA² = CB x CD.
Ans:
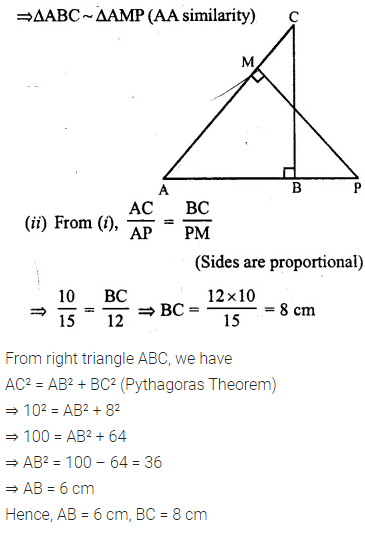
Que-14:In the given figure, ΔABC and ΔAMP are right angled at B and M respectively. Given AC = 10 cm, AP = 15 cm and PM = 12 cm. (i) Prove ΔABC ~ ΔAMP (ii) Find AB and BC.
Ans: (i) In ΔABC and ΔAMP,
∠A = ∠A (Common)
∠ABC = ∠AMP (Each = 90°)
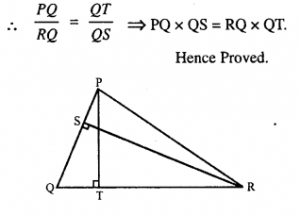
Que-15: Given : RS and PT are altitudes of ΔPQR prove that: (i) ΔPQT ~ ΔQRS, (ii) PQ x QS = RQ x QT.
Ans: Proof: In ΔPQT and ΔQRS,
∠PTQ = ∠RSQ (Each = 90°)
∠Q = ∠Q (Common)
ΔPQT ~ ΔQRS (AA postulate)
Que-16: Given : ABCD is a rhombus, DPR and CBR are straight lines.
Ans: Proof: In ΔAPD and ΔPRC
∠DPA = ∠CPR (Vertically opposite angles)
∠PAD = ∠PCR (Alternate angles)
ΔAPD ~ ΔPRC (AA Postulate)

Que-17: Given: FB = FD, AE ⊥ FD and FC ⊥ AD. Prove : FB/AD = BC/ED
Ans:
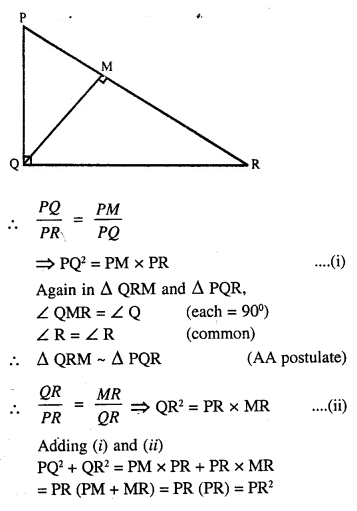
Que-18: In ΔPQR, ∠Q = 90° and QM is perpendicular to PR, Prove that:
(i) PQ² = PM x PR
(ii) QR² = PR x MR
(iii) PQ² + QR² = PR²
Ans: Given: In ΔPQR, ∠Q =90°
QM ⊥ PR.
To Prove:
(i) PQ2 = PM x PR
(ii) QR2 = PR x MR
(iii) PQ2 + QR2 = PR2
Proof: In ΔPQM and ΔPQR,
∠QMP = ∠PQR (each = 90°)
∠P = ∠P (Common)
ΔPQM ~ ΔPQR (AA postulate
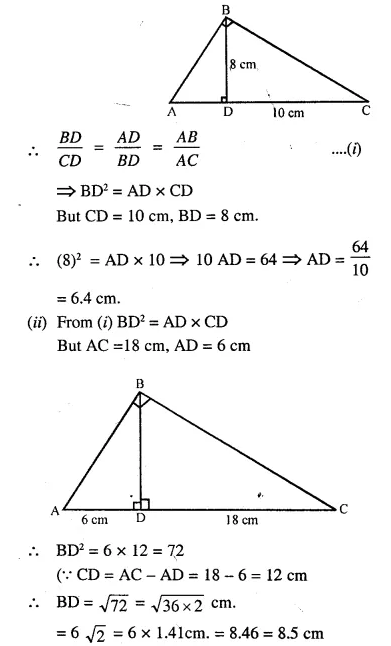
Que-19: In ΔABC, ∠B = 90° and BD x AC.
(i) If CD = 10 cm and BD = 8 cm; find AD.
(ii) If AC = 18 cm and AD = 6 cm; find BD.
(iii) If AC = 9 cm, AB = 7 cm; find AD.
Ans: In ΔABC, ∠B = 90°
∠A + ∠C = 90° …….(i)
and in ΔBDC, ∠D = 90°
∠CBD + ∠C = 90° ….(ii)
From (i) and (ii)
∠A + ∠C = ∠CBD + ∠C
∠A = ∠CBD
Similarly ∠C = ∠ABD
Now in ΔABD and ΔCBD,
∠A = ∠CBD and ∠ABD = ∠C
ΔABD ~ ΔCBD (AA Postulate)

Que-20: In the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm. L is a point on PR such that RL : LP = 2 : 3. QL produced meets RS at M and PS produced at N. find……………RM
Ans: In ΔLNP and ΔRLQ
∠LNP = ∠LQR (Alternate angles)
∠NLP = ∠QLR (Vertically opposite angles)
ΔLNP ~ ΔRLQ (AA Postulate)

Que-21: In quadrilateral ABCD, diagonals AC and BD intersect at point E. Such that AE : EC = BE : ED. Show that ABCD is a parallelogram.
Ans: Given : In quadrilateral ABCD, diagonals AC and BD intersect each other at E and

Que-22: In ΔABC, AD is perpendicular to side BC and AD² = BD x DC. Show that angle BAC = 90°
Ans: Given: In ΔABC, AD x BC and AD² = BD x DC
To Prove: ∠BAC = 90°

Que-23: In the given figure AB || EF || DC; AB = 67.5 cm. DC = 40.5 cm and AE = 52.5 cm. (i) Name the three pairs of similar triangles. (ii) Find the lengths of EC and EF.
Ans: (i) In the figure AB || EF || DC
There are three pairs of similar triangles.
(i) ΔAEB ~ ΔDEC
(ii) ΔABC ~ ΔEEC
(iii) ΔBCD ~ ΔEBF
(ii) ΔAEB ~ ΔDEC

Que-24: In the given figure, QR is parallel to AB and DR is parallel to QB. Prove that PQ² = PD x PA.
Ans: Given: In the figure QR || AB mid DR || QB.
To Prove: PQ² = PD x PA
Proof— In ΔPQB,
DR || QB (given)

Que-25: Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that : EL = 2 BL.
Ans:

Que-26: In the figure given below P is a point on AB such that AP : PB = 4 : 3. PQ is parallel to AC. (i) Calculate the ratio PQ : AC, giving reason for your answer. (ii) In triangle ARC, ∠ARC = 90° and in triangle PQS, ∠PSQ = 90°. Given QS = 6 cm, calculate the length of AR. [1999]
Ans: Given: In ΔABC, P is a point on AB such that AP : PB = 4 : 3
and PQ || AC is drawn meeting BC in Q.
CP is joined and QS ⊥ CP and AR ⊥ CP
To Find:
(i) Calculate the ratio between PQ : AC giving reason.
(ii) In ΔARC ∠ARC= 90°
and In ΔPQS, ∠PSQ = 90°, if QS = 6 cm, calculate AR.
proof:
(i) In ΔABC, PQ || AC.
Que-27: In the right angled triangle QPR, PM is an altitude Given that QR = 8 cm and MQ = 3.5 cm. Calculate, the value of PR. Given: In right angled ΔQPR, ∠P = 90° PM ⊥ QR, QR = 8 cm, MQ = 3.5 cm. Calculate PR [2000]
Ans: In ΔPQM and ΔQPR,
∠PMQ = ∠QPR (each = 90°)
∠Q = ∠Q (common)
ΔPQM ~ ΔQPR (AA postulate)

Que-28: In the figure given below, the medians BD and CE of a triangle ABC meet at G. Prove that (i) ΔEGD ~ ΔCGB (ii) BG = 2 GD from (i) above.
Ans: Given: In ΔABC, BD and CE are the medians of sides AC and AB respectively which intersect each at G.
To Prove:
(i) ΔEGD ~ ΔCGB
(ii) BG = 2 GD.
Proof: D and E are the mid points of AC and AB respectively.

–: Similarity Exercise Exe-15A Class-10 Concise ICSE Maths Solution Ch-15. :–
Return to :- Selina Concise Solutions for ICSE Class-10 Maths
Thanks
Please Share with Your Friends