Simple Harmonic Motion Numerical on Springs Class-11 Nootan ISC Physics Ch-23 Simple Harmonic Motion. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-11 Physics.
Simple Harmonic Motion Numerical on Springs Class-11 Nootan ISC Physics Ch-23 Simple Harmonic Motion
| Board | ISC |
| Class | 11 |
| Subject | Physics |
| Book | Nootan |
| Chapter-23 | Simple Harmonic Motion. |
| Topics | Numericals on Springs of SHM |
| Academic Session | 2025-2026 |
Numericals on Springs of SHM
Class-11 Nootan ISC Physics Ch-23 Simple Harmonic Motion. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan
Q-21: When a 2.0 kg body is suspended by a spring, the spring is stretched. If the body is pulled down slightly and released, it oscillates up and down. What force is applied on the body by the spring when it passes through the mean position?
Ans: When the spring is at its mean position, force applied by the spring will be equal to weight suspended
=> mg = 2 x 9.8 = 19.6 N
Q-22: A weight of 1 kg suspended by a light spring performs 4 oscillations in 1 second. How many oscillations per second will be performed by a weight of 4 kg suspended by the same spring?
Ans: n1 / n2 = √m2 / m1
=> 4 / n2 = √4 / 1
=> n2 = 2
Q-23: The force-constant of an ideal spring is 200 N m^-1. A body of mass (200/π²) kg is suspended from it and is made to oscillate. Find the time-period of the oscillation.
Ans: T = 2 π √m/k
=> 2π √200/π² x 200 = 2 s
Q-24: The length of a spring increases by 20 cm when a 1 kg body is suspended from it. Determine the force constant of the spring. If the body is pulled down slightly and then released, what will be the period of oscillations? If this body along with the spring executes SHM on a frictionless horizontal surface, then what will be the time-period?
Ans: F = k x
=> 9.8 = k x . 2
=> k = 49 N m^-1
T = 2 π √m / k
=> 2 π √1 / 49
=> 2 π / 7 = 0.9 s
T = 0.9 s (oscillations of spring is independent of gravity)
Q-25: On suspending a 0.5 kg body by a spring of negligible mass, the spring stretches by 7 cm. Now, the body is given a velocity of 40 cm^-1 s downwards from its mean position. Calculate the angular velocity and the amplitude of the resulting oscillatory motion.
Ans: F = k x
=> 0.5 x 9.8 = k x 7 x 10^-2
=> k = 0.5 x 9.8 / 7 x 10^-2 = 70 N m^-1
again energy = 1/2 m v² = 1/2 m ω² a²
=> v = ω a
=> v = √k/m . a
=> 0.4 = √70/0.5 x a
=> a = 3.4 cm
and ω = √k/m = √70/0.5 = √140 = 11.8 rad/s
Q-26: The force-constant of a weightless spring is 16 N m^-1. A body of mass 1.0 kg is suspended by it. The body is pulled down through 5 cm and then left free. Determine: (i) period of oscillation of the body, (ii) maximum potential energy of the spring.
Ans: T = 2 π √m / k = 2 π√1 / 16 = 1.57 s
max P.E. = 1/2 m ω² a²
=> 1/2 m x k/m a²
=> 1/2 k a²
=> 1/2 x 16 x (5 x 10^-2)² = 2 x 10^-2 J
Q-27: When the length of a spring is altered by 0.1 m, the potential energy of the spring changes the force-constant of the spring.
Ans: ΔU = 1/2 k (Δx)²
=> k = ΔU x 2 / (Δx)²
=> k = 0.5 x 2 / (0.1)² = 100 N m^-1
Q-28: Two bodies P (mass 2 kg) and Q P (mass 1 kg) are rigidly connected by a spring of force-constant 200 Nm^-1. From the rest position, the body P is compressed downwards by a distance of 2 cm. Calculate the frequency of oscillation of P and also the oscillation energy.
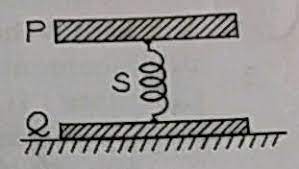
Ans: f = (1 / 2π) √k/m
=> (1 / 2π) √200 / 2
=> 5 / π Hz
energy = 1/2 k x²
=> 1/2 x 200 x (0.2)² = 0.04 J
Q-29: The period of oscillation of a mass m suspended by an ideal spring is 2 s. If an additional mass of 21 suspended, the time-period is increased by 1 s. Find the value of m.
Ans: T1 / T2 = √m1 / m2
=> (2 / 3) = √ m / (m + 2)
=> (4 / 9) = m / (m + 2)
=> m = 1.6 kg
Q-30: A 2.0 kg body is suspended by a spring. When in addition to it, another body of 300 g is suspended, the spring further stretches by 2.0 cm.If the second body is removed and the first body is made to oscillate, then what will be the time-period?
Ans: ΔF = k Δx
=> 0.3 x 9.8 = k x .02
=> k = 147 N m
∴T = 2 π √m/k
=> 2 π √2 / 147 = 0.73 s
Q-31: A 10 kg body is suspended by an ideal spring (force- constant 250 N m^-1). (i) Calculate the time-period of the body. (ii) If the body is displaced downwards by 30 cm and released, with what speed will it pass through its mean position? (iii) What is the total energy in the body? (iv) How much time it takes in reaching its mean position from its position of maximum displacement?
Ans: T = 2 π √m/k
=> 2 π √10 / 250 = 1.256 s
(v)max = a ω
=> a x 2 π / T
=> 0.3 x 2 x 3.14 / 1.256 = 1.50 m s^-1
Total Energy = 1/2 m (v)²max
=> 1/2 x 10 x (1.5)² = 11.25 J
t = T / 4
=> 1.256 / 4 = 0.314 s
Q-32: A 10 kg body is suspended by a weightless spring (force-constant 250 N m^-1). If the body is displaced downwards by 40 cm and released, then determine: (i) time-period of the body, (ii) maximum speed of the body and (iii) total energy of the spring- body system.
Ans: T = 2 π √m/k
=> 2 π √10 / 250 = 1.256 s
v = a ω
=> 0.4 x 2 π / 1.256 = 2.0 m s^-1
E = 1/2 m v²
=> 1/2 x 10 x (2)² = 20 J
Q-33: A body of mass 0.2 kg, when suspended by a spring, increases the length of the spring by 4.9 cm. If the poi spring obeys Hooke’s law, then determine: (i) the period of oscillation of the spring when a body of 0.4 kg is suspended by it and (ii) the change in accumulated energy of the spring when its extension changes from 4.9 cm to 9.8 cm.
Ans: F = k x
=> m g = k x
=> k = m g / k x = 0.2 x 9.8 / 4.9 x 10^-2 = 40 N m^-1
T = 2 π √m/k
=> 2 π √0.4 / 40 = 2 π / 10 = 0.628 s
ΔU = 1/2 k (x2² – x1²)
=> 1/2 x 40 ((9.8 x 10^-2)² – (4.9 x 10^-2)²) = 0.144 J
Q-34: A particle which is attached to a spring oscillates horizontally with simple harmonic motion with a frequency of 1/π Hz and total energy of 10 J. If the maximum speed of the particle is 0.4 m s^-1, what is the force-constant of the spring? What will be the maximum potential energy of the spring during the motion.
Ans: ω . a = 0.4
1/2 m ω² a² = 10
=> m x (0.4)² = 20
=> m = 20 / (0.4)² = 125 kg
ω = √k/m
k = ω² – m
=> 125 x (2 π x 1 / π)² = 500 N m^-1
(U)max = Total Energy = 10 J
Q-35: A small body of mass 0.10 kg is executing simple harmonic motion whose amplitude is 1.0 m and the period is 0.20 s. What is the maximum value of the force acting on it? If oscillations are performed by means of a spring then what will be the force-constant of the spring?
Ans: m = 0.1 kg a = 1 m T = 0.2 s
ω = 2 π / T
=> 2 π / 0.2 = 10 π
(f)max = m ω² a
=> 0.1 x 1 π² ω x 1 = 98.6 N
k = f / a
=> 98.6 / 1.0 = 98.6 N
— : End of Simple Harmonic Motion Numerical on Springs Class-11 Nootan ISC Physics Ch-23 .. :–
Return to : – – Nootan Solutions for ISC Physics Class-11
Thanks
Please share with your friends


