ML Aggarwal Simultaneous Linear Equations Exe-5.1 Class 9 ICSE Maths Solutions. Step by step solutions  of  Simultaneous Linear Equations problems as council prescribe guideline. Visit official website CISCE for detail information about ICSE Board Class-9.

ML Aggarwal Simultaneous Linear Equations Exe-5.1 Class 9 ICSE Maths Solutions

Board	ICSE
Subject	Maths
Class	9th
Chapter-5	Simultaneous Linear Equations
Topics	Solution of Exe-5.1 Questions
Academic Session	2024-2025

Solution of Exe-5.1 Questions

ML Aggarwal Simultaneous Linear Equations Exe-5.1 Class 9 ICSE Maths Solutions

Solve the following system of simultaneous linear equations by the substitution method:

Question 1.

(i) x + y = 14

x – y = 4

(ii) s – t = 3

s/3 + t/2 = 6

(iii) 2x + 3y = 9

3x + 4y = 5

(iv) 3x – 5y = 4

9x – 2y = 7

Answer :

(i) x + y = 14

x – y = 4

It can be written as

x = 4 + y

By substituting the value in the above equation

4 + y + y = 14

By further calculation

2y = 14 – 4 = 10

Dividing by 2

y = 10/2 = 5

So we get

x = 4 + 5 = 9

Hence, x = 9 and y = 5.

(ii) s – t = 3

s/3 + t/2 = 6

By taking LCM

2s + 3t = 6 × 6 = 36

We know that

s – t = 3 …. (1)

2s + 3t = 36 ….. (2)

So we get

s = 3 + t …. (3)

By substituting the value of s in equation (2)

2 (3 + t) + 3t = 36

By further calculation

6 + 2t + 3t = 36

So we get

5t = 36 – 6 = 30

By division

t = 30/5 = 6

Substituting t in equation (3)

s = 3 + 6 = 9

Hence, s = 9 and t = 6.

(iii) 2x + 3y = 9 …. (1)

3x + 4y = 5 ….. (2)

Equation (1) can be written as

2x = 9 – 3y

x = (9 – 3y)/ 2 …. (3)

By substituting the value of x in equation (2)

3 × (9 – 3y)/ 2 + 4y = 5

By further calculation

(27 – 9y)/ 2 + 4y = 5

By taking LCM

27 – 9y + 8y = 10

So we get

-y = – 17

y = 17

Substituting y in equation (3)

x = [9 – (3 × 17)]/ 2

By further calculation

x = (9 – 51)/ 2

x = – 21

Hence, x = – 21 and y = 17.

(iv) 3x – 5y = 4 ….. (1)

9x – 2y = 7 …. (2)

Multiply equation (1) by 3

9x – 15y = 12

9x – 2y = 7

By subtracting both the equations

– 13y = 5

y = -5/13

Equation (1) can be written as

3x – 5y = 4

x = (4 + 5y)/ 3 ….. (3)

By substituting the value of x in equation (2)

9 [(4 + 5y)/ 3] – 2y = 7

By further calculation

12 + 15y – 2y = 7

13y = – 5

So we get

y = -5/13

Substituting y in equation (3)

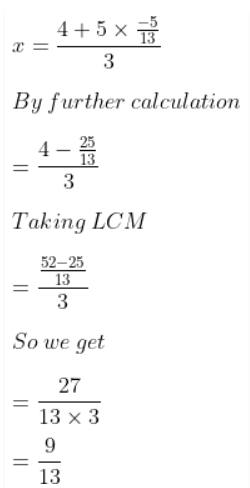
Hence, x = 9/13 and y = – 5/13.

Question 2.

(i) a + 3b = 5

7a – 8b = 6

(ii) 5x + 4y – 4 = 0

x – 20 = 12y

Answer :

(i) a + 3b = 5 …. (1)

7a – 8b = 6 ….. (2)

Now multiply equation (1) by 7

7a + 21b = 35 …. (3)

7a – 8b = 6 ….. (4)

By subtracting both the equations

29b = 29

So we get

b = 29/29 = 1

Now substituting b = 1 in equation (1)

a + 3 (1) = 5

By further calculation

a + 3 = 5

So we get

a = 5 – 3 = 2

Therefore, a = 2 and b = 1.

(ii) 5x + 4y – 4 = 0

x – 20 = 12y

We can write it as

5x + 4y = 4 …. (1)

x – 12y = 20 ….. (2)

Now multiply equation (2) by 5

5x + 4y = 4 …. (3)

5x – 60y = 100

By subtracting both the equations

64y = – 96

So we get

y = -96/64 = – 3/2

Now substitute the value of y in equation (1)

5x + 4 (-3/2) = 4

By further calculation

5x + 2 (-3) = 4

So we get

5x – 6 = 4

5x = 4 + 6 = 10

By division

x = 10/5 = 2

Therefore, x = 2 and y = – 3/2.

Question 3.

(i) 2x – 3y/4 = 3

5x – 2y – 7 = 0

(ii) 2x + 3y = 23

5x – 20 = 8y

Answer :

(i) 2x – 3y/4 = 3

5x – 2y – 7 = 0

We can write it as

2x/1 – 3y/4 = 3

By taking LCM

(8x – 3y)/ 4 = 3

By cross multiplication

8x – 3y = 12 ….. (1)

5x – 2y = 7 …. (2)

Now multiply equation (1) by 2 and (2) by 3

16x – 6y = 24

15x – 6y = 21

By subtracting both the equations

x = 3

Now substituting the value of x in equation (1)

8 × 3 – 3y = 12

By further calculation

24 – 3y = 12

– 3y = 12 – 24

So we get

– 3y = – 12

y = – 12/-3 = 4

Therefore, x = 3 and y = 4.

(ii) 2x + 3y = 23

5x – 20 = 8y

We can write it as

2x + 3y = 23 …. (1)

5x – 8y = 20 …. (2)

By multiplying equation (1) by 5 and equation (2) by 2

10x + 15y = 115

10x – 16y = 40

By subtracting both the equations

31y = 75

So we get

y = 75/31 = 2 13/31

By substituting the value of y in equation (1)

2x + 3 (75/31) = 23

By further calculation

2x + 225/31 = 23

We can write it as

2x = 23/1 – 225/31

Taking LCM

2x = (713 – 225)/ 31 = 488/31

So we get

x = 488/ (31 × 2) = 244/ 31 = 7 27/31

Therefore, x = 7 27/31 and y = 2 13/31.

Question 4.

(i) mx – ny = m² + n²

x + y = 2m

(ii) 2x/a + y/b = 2

x/a – y/b = 4

Answer :

(i) mx – ny = m² + n² …. (1)

x + y = 2m …. (2)

We can write it as

x = 2m – y ….. (3)

Now substitute the value of x in (1)

m (2m – y) – ny = m² + n²

By further calculation

2m² – my – ny = = m² + n²

Taking out y as common

m² – y (m + n) = n²

It can be written as

m² – n² – y (m + n) = 0

Expanding using formula

(m – n) (m + n) – y (m + n) = 0

Taking (m + n) as common

(m + n) [(m – n) – y] = 0

So we get

m – n – y = 0

y = m – n

From equation (3)

x = 2m – (m – n)

By further calculation

x = 2m – m + n = m + n

Hence, x = m + n and y = m – n.

(ii) 2x/a + y/b = 2 …. (1)

x/a – y/b = 4 …. (2)

Adding both the equations

3x/a = 6

So we get

x = 6a/3 = 2a

Substituting x in equation (1)

2 (2a)/ a + y/b = 2

By further calculation

4a/a + y/b = 2

So we get

4 + y/b = 2

y/b = 2 – 4 = – 2

Here

y = – 2b

Therefore, x = 2a and y = – 2b.

Question 5. Solve 2x + y = 35, 3x + 4y = 65. Hence, find the value of x/y.

Answer :

It is given that

2x + y = 35 …. (1)

3x + 4y = 65 ….. (2)

Now multiply equation (1) by 4

8x + 4y = 140 …. (3)

3x + 4y = 65 …. (4)

By subtracting both the equations

5x = 75

x = 75/5 = 15

Now substituting the value of x in equation (1)

8 × 15 + 4y = 140

By further calculation

120 + 4y = 140

4y = 140 – 120

So we get

4y = 20

y = 20/4 = 5

Here

x/y = 15/5 = 3

Therefore, x/y = 3.

Question 6. Solve the simultaneous equations 3x – y = 5, 4x – 3y = – 1. Hence, find p, if y = px – 3.

Answer :

It is given that

3x – y = 5 ….. (1)

4x – 3y = – 1 ….. (2)

Now multiply equation (1) by 3

9x – 3y = 15 ….. (3)

4x – 3y = – 1 ….. (4)

Subtracting equation (3) and (4)

5x = 16

x = 16/5

Substitute the value of x in equation (3)

3 × 16/5 – y = 5

By further calculation

48/5 – y = 5

48/5 – 5 = y

Taking LCM

(48 – 25)/ 5 = y

So we get

y = 23/5

We know that

y = px – 3

23/5 = p × 16/5 – 3

Substitute the value of x and y

23/5 + 3 = 16p/5

Taking LCM

(23 + 15)/ 5 = 16p/5

By further calculation

38/5 = 16p/5

So we get

16p = 38

p = 19/8

Therefore, x = 16/5, y = 23/5 and p = 19/8.

—  : End of ML Aggarwal Simultaneous Linear Equations Exe-5.1 Class 9 ICSE Maths Solutions :–

Return to :- ML Aggarawal Maths Solutions for ICSE  Class-9

Thanks

Please Share with Your Friends