Superposition of Stationary Waves Numerical Class-11 Nootan ISC Physics Ch-28 Superposition of Waves-2 : Stationary (Standing) Waves : Vibration of Air Columns. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-11 Physics.
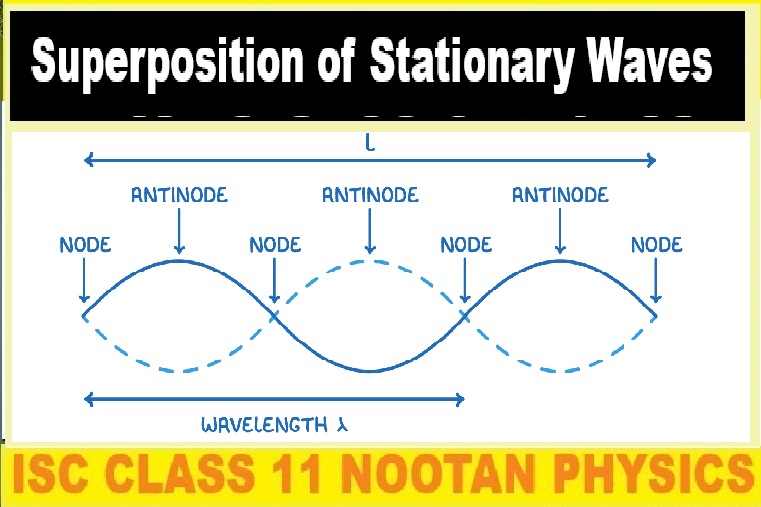
Superposition of Stationary Waves Numerical Class-11 Nootan ISC Physics Ch-28 Superposition of Waves-2: Stationary (Standing) Waves: Vibration of Air Columns
| Board | ISC |
| Class | 11 |
| Subject | Physics |
| Book | Nootan |
| Chapter-28 | Superposition of Waves-2 : Stationary (Standing) Waves : Vibration of Air Columns |
| Topics | Numericals on Superposition of Stationary Waves |
| Academic Session | 2025-2026 |
Numericals on Superposition of Stationary Waves
Numerical Class-11 Nootan ISC Physics Ch-28 Superposition of Waves-2 : Stationary (Standing) Waves : Vibration of Air Columns
Q-1: The equation of a progressive wave is y = 0.09 sin 8 π [t- (x/20)]. On striking a rigid wall the amplitude of the reflected wave becomes 2/3rd of its initial value. Determine: (i) the equation of the reflected wave, (ii) the displacement equation of the particle at x = 0 in the reflected wave.
Ans-1 Equation of wave y = 0.09 sin 8 π [t- (x/20)]
when striking a rigid wall the amplitude is a’ = (2/3)a
=> 2/3 x 0.09 = 0.06
(i) The equation of reflected wave
y = – a’ sin 8 π [t- (x/20)]
=> – 0.06 sin 8 π [t- (x/20)]
(ii) The displacement equation of the particle at x = 0
y = – 0.06 sin 8 π (t- 0)
=> – 0.06 sin 8 π t
Q-2: The equation of a plane progressive wave is y = 0.02 sin 2 π (330 t-x). (i) If this wave is reflected from a rigid end, then what will be the equation of the reflected wave? The amplitude remains 60% after the reflection. (ii) If the wave is reflected from a free end and the amplitude remains 75%, then what will be the equation of the reflected wave?
Ans-2 y = 0.02 sin 2 π (330 t-x)
(i) when the wave reflected rigid end then a’ = 60% of a
=> 60 / 100 x 0.02 = 0.012
then equation y = – a’ sin 2 π (330 t + x)
=> y = – 0.012 sin 2 π (330 t + x)
(ii) when the reflected wave from a free end then
y = a’ sin 2 π (330 t + x)
a’ = 75 % of a = 75 / 100 x 0.02 = 0.015
y = 0.015 sin 2 π (330 t + x)
Q-3: The equation of a stationary wave is y = 4 cos (π x/3) sin 40 πt, where x and y are in cm and t in second. Determine the amplitude, frequency and speed of the progressive waves producing it. What is the distance between two consecutive nodes?
Ans-3 Equation y = 4 cos (π x/3) sin 40 πt ——-(i)
Comparing eq.1 by y = 2 a cos (2 π x / λ) sin 2 π t / T we have
2 a = 4
=> a = 2 cm
2 π x / λ = π x / 3
=> λ = 2 x 3 = 6 cm
and 2 π t / T = 40 π t
=> T = 1 / 20
amplitude a = 2 cm
frequency n = 20 s^-1
Speed v = n x λ = 20 x 6 = 120 cm / s
Distance between two consecutive nodes = λ / 2 = 6 / 2 = 3 cm
Q-4: The equation of wave a longitudinal stationary produced in a closed organ pipe is y = 6 sin (2 π x/6) cos(160 πt), where x, y expressed in cm and t in second. Find: (i) the frequency, amplitude and wavelength of the original progressive wave, (ii) separation between two consecutive antinodes, (iii) equation of the original progressive wave. are
Ans-4 Equation y = 6 sin (2 π x/6) cos(160 πt) ——-(i)
Comparing eq.1 by y = 2 a sin (2 π x / λ) cos(2 π t / T) we have
2 a = 6
=> a = 3
2 π x / λ = 2 π x/6
=> λ = 6 cm
2 π t / T = 160 πt
=> n = 80 Hz
(i) frequency n = 80 Hz
amplitude a = 3 cm
wavelength λ = 6 cm
(ii) Separation between two consecutive antinodes = λ / 2 = 6 / 2 = 3 cm
(iii) Equation of original progressive wave
y = a sin (2 π x / λ – 2 π t / T)
=> 3 sin (2 π x / 6 – 2 π t / (1 / 80))
=> 3 sin ( π x / 3 – 160π t)
Q-5: The distance between two consecutive nodes in a stationary wave is 25 cm. If the speed of the wave be 300 m s^-1, calculate the frequency.
Ans-5 Given λ / 2 = 25 cm
=> λ = 50 cm = 0.5 m
v = 300 m / s
frequency n = v / λ = 300 / 0.5 = 600 Hz
— : End of Superposition of Stationary Waves Numerical Class-11 Nootan ISC Physics Ch-28 Superposition of Waves-2 : Stationary (Standing) Waves : Vibration of Air Columns :–
Return to : – – Nootan Solutions for ISC Physics Class-11
Thanks
Please share with your friends


