Total Internal Reflection Numerical Class-12 Nootan ISC Physics Solution Ch-15 Refraction of Light at a Plane Interface : Total Internal Reflection : Optical Fiber. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-12 Physics.
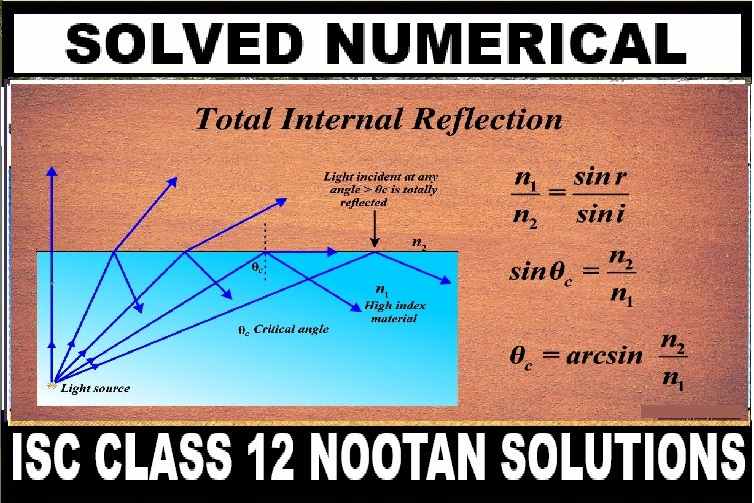
Total Internal Reflection Numerical Class-12 Nootan ISC Physics Solution Ch-15 Refraction of Light at a Plane Interface : Total Internal Reflection : Optical Fiber
| Board | ISC |
| Class | 12 |
| Subject | Physics |
| Book | Nootan |
| Chapter-15 | Refraction of Light at a Plane Interface |
| Topics | Numericals on Total Internal Reflection |
| Academic Session | 2025-2026 |
Numericals on Total Internal Reflection
Class-12 Nootan ISC Physics Solution Ch-15 Refraction of Light at a Plane Interface : Total Internal Reflection : Optical Fiber.
Que-13: In total internal reflection when the angle of incidence is equal to the critical angle for the pair of media in contact, what will be angle of refraction?
Ans- When the angle of incidence is equal to the critical angle for a given pair of media, the angle of refraction becomes 90°. This
means that the refracted ray does not enter the second medium but instead travels along the boundary between the two media.
Que-14: Critical angle for total internal reflection from a medium to vacuum is 60°. Find the velocity of light in the given medium.
Ans- critical angle
sin θc = n2/n1
=>sin 60 = 1/n1
=> n1 = 2√3/3
we know that, v = c/n
=> v = 3 x 10^8 / (2√3/3)
=> v = 2.6 x 10^8 m/s
Que-15: A ray of light falls normally on the face of a glass prism (n = 1.5). Find the angle of the prism, if the ray just fails to emerge from the second face.
Ans- Applying Snell’s law
n sin i = 1 x sin 90°
=> 1.5 sin i = 1
sin i = 1/1.5 = 41.8°
Que-16: A substance has a critical angle of 45° for yellow light. What is the refractive index of the substance?
Ans- n = 1/sin ic = 1/sin 45° = √2
=> n = 1.414
Que-17: The refractive index of glass relative to air is 1.5. What is critical angle for glass-air interface?
Ans- ic = sin^-1 1/μ = sin^-1 1/1.5
=> sin^-1 0.6 = 41.8°
Que-18: What is the critical angle for a light ray going from dense glass into water? The refractive indices of dense glass and water relative to air are 1.62 and 1.33 respectively.
Ans- ic = sin^-1(μ1/μ2) μ1<μ2
=> ic = sin^-1 (1.33/1.62) = 55°
Que-19: The absolute refractive indices of water and glycerine are 1.33 and 1.46 respectively. Find the critical angle for a ray travelling from glycerine into water.
Ans- ic = sin^-1(μ1/μ2) μ1<μ2
=> ic = sin^-1 (1.33/1.46) = 65.5°
Que-20: An equilateral prism of glass of refractive index 1.45 is immersed in water of refractive index 1.33. A narrow beam of light falls normally on one face of the prism. Find the angle of emergence of the beam.
Ans- i = 90° – 30° = 60° , n = 1.33
Applying Snell’s law
1.45 x sin 60° = 1.33 sin e
=> 1.45 x √3 / 2 x 1.33 = sin e
sin e = 0.944
e = sin^-1 0.944 = 70.8°
Que-21: A small bulb is placed at the bottom of a tank containing water to a depth of 80 cm. What is the area of the surface of water through which light of the bulb can emerge out? Refractive index of water is 1.33. Consider the bulb to be a point-source.
Ans- n = 1/ sin ic
=> 1.33 = √(h²+r²)/r
=> 4/3 = √(h²+r²)/r
=> 16/9 = (h²+r²)/r² = h²/r² -1
=> r² = 9 x 0.8 x 0.8 / 7
=> ∴area = πr² = 3.14 x 7 x 0.8 x 0.8 / 7 = 2.6 m²
Que-22: A point-source of light is placed at the centre of the bottom of a jar having a liquid of refractive index 5/3. An opaque disc of radius 1.0 cm is placed on the liquid surface with its centre vertically above the source. What is the maximum height of the liquid for which the source is not visible from above?
Ans- from previous question
=> 5/3 = √(h²+r²)/r
=> 25/9 = h²/r² +1
=> h² = 16/9
=> h = 4/3 cm
— : End of Total Internal Reflection Numerical Class-12 Nootan ISC Physics Solution Ch-15 .–
Return to : – Nootan Solutions for ISC Class-12 Physics
Thanks
Please share with your friend


