Vibration of Stretched Springs Numerical Class-11 Nootan ISC Physics Solutions Ch-29 Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-11 Physics.

Vibration of Stretched Springs Numerical Class-11 Nootan ISC Physics Solutions Ch-29
| Board | ISC |
| Class | 11 |
| Subject | Physics |
| Book | Nootan |
| Chapter-29 | Vibration of Stretched Springs |
| Topics | Numericals on Standing Waves in Strings and Laws of Vibrations of Stretched Strings |
| Academic Session | 2025-2026 |
Numericals on Standing Waves in Strings and Laws of Vibrations of Stretched Strings
Class-11 Nootan ISC Physics Solutions Ch-29
Q-1: The fundamental frequency of the transverse vibrations of a stretched string is 500 Hz. If the tension of the string is made four times, then calculate its fundamental frequency.
Ans-

Q-2: The frequency of a steel wire of a fixed length and diameter at a tension of 576 N is 480 Hz. Calculate the frequency of the wire at a tension of 144 N.
Ans-
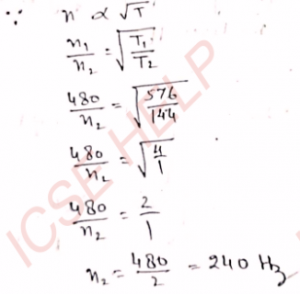
Q-3: The mass of a 1 metre wire of steel is 20 g. The wire is stretched under a tension of 800 N. What are the frequencies of its fundamental mode of vibration and the next three higher modes?
Ans-

Q-4: Two stretched strings give 3 beats per second. The frequency of one of them is 440 Hz. (a) What are possible frequencies of the other string? (b) What is the possible frequency of the other string, if on increasing the tension of this string the frequency of beats decreases?
Ans-
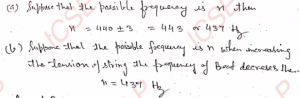
Q-5: A and B are two wires whose fundamental frequencies are 256 and 382 Hz respectively. How many beats in two seconds will be heard by the third harmonic of A and the second harmonic of B?
Ans-
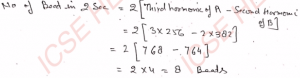
Q-6: The frequency of the fundamental tone of 1 metre long wire of a sitar is 256 Hz. At how much distance from the upper end should the wire be pressed to produce a note of frequency 384 Hz?
Ans-

Q-7: When a wire has a tension of 10 kg-wt, then its fundamental frequency is 256 Hz. (a) At what tension will its frequency become 512 Hz? (b) If the tension be kept 10 kg wt then how can the frequency of the wire be changed to 768 Hz?
Ans-

Q-8: A uniform wire is stretched between two bridges situated at a distance of 1.0 m. The wire is fixed at one end and its other end passes over a pulley and carries a weight of 9 kg. The fundamental frequency of the wire is 750 Hz. (a) Find the speed of sound in the wire. (b) If the weight is reduced to 4 kg, then what will be the speed, wavelength and frequency?
Ans-

Q-9: If the tension in a stretched string is increased by 5 kg-wt, the frequency of its fundamental tone increases in the ratio 2: 3. What was the initial tension in the string?
Ans-

Q-10: The length of a wire between two ends of a sonometer is 105 cm. Where should the two bridges be placed so that the fundamental frequencies of the three segments are in the ratio of 1 : 3 : 15.
Ans-

Q-11: Two wires whose lengths are in the ratio 3: 2, when stretched by equal weights, produce the same note. If the wires are made of different metals and their radii are in the ratio 1: 2, then determine the ratio of the densities of the two metals.
Ans-
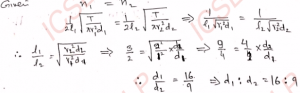
Q-12: A wire of density 9 x 10^3 kg m^-3 is stretched between two clamps 1 m apart and is subjected to an extension of 4.9 x 10^-4 m. What will be the lowest frequency of the transverse vibrations in the wire? (γ = 9 × 10^10 N m^-2)
Ans-

Q-13: Two wires A and B are stretched between two points. The diameter, tension and density of B are twice the diameter, tension and density of A. What will be the ratio of frequencies of A and B?
Ans-

Q-14: A and B are two wires stretched under the same tension. The length of A is twice the length of B, and the diameter of A is half the diameter of B. If the density of A is 0.09 times the density of B, then compare the frequencies of A and B.
Ans-

Q-15: A wire has a length of 100 cm and a mass of 0.4 g. If a 5 kg weight has been suspended from the wire and the wire is vibrating in two segments, then determine the frequency of the note emitted by the wire.
Ans-

Q-16: The frequency of the fundamental note of a 66 cm long open tube is the same as that of a 20 cm long stretched wire whose mass is 0.1 g cm¹. If the speed of sound in air is 330 m s^-1, then determine the tension in the wire.
Ans-

Q-17: A tuning fork of frequency 256 Hz is in unison with a certain length of a sonometer wire. On increasing the length of the wire, 10 beats/s are produced. Calculate the frequency of the wire of increased length.
Ans-
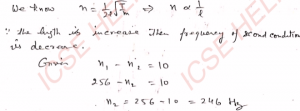
Q-18: A tuning fork produces 5 beats/second with a sonometer wire of length 40 cm. When the length of the wire is decreased by 1 cm, again the same number of beats per second are heard. Calculate the frequency of the fork.
Ans-

Q-19: The frequency of a brass wire is 240 Hz when its tension is 625 N. If its tension is decreased to 100 N and length halved, what will be its frequency?
Ans-

Q-20: The frequency of a sonometer wire is 100 Hz. On doubling the length of the wire and changing the tension, the frequency becomes 75 Hz. Determine the ratio of the initial and final tensions.
Ans-

Q-21: The ratio of frequencies of two wires having same length and same tension and made of the same material is 2 : 3. If the diameter of one wire be 0.09 cm, then determine the diameter of the other.
Ans-

Q-22: Two forks A and B when sounded together produce 4 beats/second. The fork A is in unison with 30 cm length of a sonometer wire and B is in unison with 25 cm length of the same wire at the same tension. Calculate the frequencies of the forks.
Ans-

Q-23: A weight is suspended from a sonometer wire. When the length of the wire between the bridges is 80 cm, the wire is found in unison with a tuning fork. But when an additional 0.1 kg weight is suspended from it then, to keep it in unison with the same fork, its length between the bridges is to be increased by 1 cm. What weight was suspended from the wire in the beginning?
Ans-

Q-24: A tuning fork is marked 256 number. What does it indicate? It is in unison with the wire of a sonometer whose length is 81 cm and which is under a tension of 4 kg. How can this wire be brought in unison with a fork marked 384 by (i) changing the tension only, (ii) changing the length only?
Ans-

— : End of Vibration of Stretched Springs Numerical Class-11 Nootan ISC Physics Solutions Ch-29:–
Return to : – – Nootan Solutions for ISC Physics Class-11
Thanks
Please share with your friends


