ML Aggarwal Algebra Exe-9.1 Class 6 ICSE Maths Solutions

ML Aggarwal Algebra Exe-9.1 Class 6 ICSE Maths Solutions. We Provide Step by Step Answer of  Exe-9.1 Questions for Algebra as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-6.

ML Aggarwal Algebra Exe-9.1 Class 6 ICSE Maths Solutions

Board	ICSE
Publications	Avichal Publishig Company (APC)
Subject	Maths
Class	6th
Chapter-9	Algebra
Writer	ML Aggarwal
Book Name	Understanding
Topics	Solution of Exe-9.1 Questions
Edition	2023-2024

Algebra Exe-9.1

ML Aggarwal Class 6 ICSE Maths Solutions

Page-181

Question 1. Find the rule which gives the number of matchsticks required to make the following matchsticks patterns. Use a variable to write the rule.

(i) A pattern of letter T as T

(ii) A pattern of letter V as V

(iii) A pattern of letter Z as Z

(iv) A pattern of letter U as U

(v) A pattern of letter F as F

(vi) A pattern of letter S as S

Answer:

(i) Number of matchsticks required = 2n
(ii) Number of matchsticks required = 2n
(iii) Number of matchsticks required = 3n
(iv) Number of matchsticks required = 3n
(v) Number of matchsticks required = An
(vi) Number of matchsticks required = 5n

Question 2.  If there are 24 mangoes in a box, how will you write the number of mangoes in terms of the number of boxes? (use b for the number of boxes.)

Answer:

Total number of mangoes = 24b

Question 3. Anuradha is drawing a dot Rangoli (a beautiful pattern of lines joining dots). She has 8 dots in a row. How many dots will her Rangoli have for r rows? How many dots are there if there are 12 rows?

Answer:

∵ Numbers of dots in 1 row = 8
∴ Number of dots in r rows = 8 × r = 8
Number of dots in 12 rows = 12 × 8 = 96

Question 4. Anu and Meenu are sisters. Anu is 5 years younger than Meenu. Can you write Anu’s age in terms of Meenu’s age? Take Meenu’s age as x years.

Answer:

Yes! we can write Anu’s age in terms of Meenu’s age.
Age of Meenu = x
∵ Anu is 5 years younger than Meenu
∴ Age of Anu = (x – 5) years

Question 5. Oranges are to be transferred from larger boxes to smaller boxes. When a larger box is emptied, the oranges from it fill 3 smaller boxes, and still, 7 oranges are left. If the number of oranges in a small box is taken to be x, then what is the number of oranges in the larger box?

Answer:

Let the number of oranges in a smaller box be x.
∴ Number of oranges in three smaller boxes = 3x
Number of oranges remained outside = 7
∴ Number of oranges in the larger box = 3x + 7

Question 6. Harsha’s score in Mathematics is 15 more than three-fourth of her score in Science. If she scores x marks in Science, find her score in Mathemstics?

Answer:

Let the score of science be x
Harsha score’s in Mathematics = 3/4 th of x + 15
∴ Score of Harsha’s in Mathematics = 3/4x + 15

Question 7. Look at the following matchstick pattern of equilateral triangles. The triangles are not separate. Two neighbouring triangles have a common matchstick. Observe the pattern and find the rule that gives the number of matchsticks.

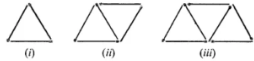
Answer:

Number of matchsticks required = 2x + 1, where x is the number of triangles.

Question 8.  Look at the following matchstick pattern of letter A. The A’s are not separate. Two neighbouring A’s have two common matchsticks. Observe the pattern and find the rule that gives the number of matchsticks.

Answer:

Number of matchsticks required = 4x + 2, where x is the number of letter ‘A’ formed.

—  : End of ML Aggarwal Algebra Exe-9.1 Class 6 ICSE Maths Solutions :–

Return to –  ML Aggarwal Maths Solutions for ICSE Class -6

Thanks