Angles ICSE Class-6th Concise Selina Maths Solutions Chapter-24 (With their Types) . We provide step by step Solutions of Exercise / lesson-24 Angles (With their Types) for ICSE Class-6 Concise Selina Mathematics.
Our Solutions contain all type Questions of Exe-24 A, Exe-24 B and Revision Exercise to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-6
Angles ICSE Class-6th Concise Selina Maths Solutions Chapter-24 (With their Types)
–: Select Topics :–
Exercise – 24 A Angles (With their Types) for ICSE Class-6th Concise Selina Maths Solutions
Question -1.
For each angle given below, write the name of the vertex, the names of the arms and the name of the angle.

Answer-1
(i) In figure (i) O is the vertex, OA, OB are its arms and name of the angle is ∠AOB or∠BOA or simply ∠O.
(ii) In figure (ii) Q is the vertex, QP and QR its arms and the name of the angle is ∠PQR or ∠RQP or simply ∠Q.
(iii) In figure (iii), M is the vertex, MN and ML and its anus, and name of the angle is ∠LMN or ∠NML or simply ∠M.
Question -2.
Name the points :
(i) in the interior of the angle PQR,
(ii) in the exterior of the angle PQR.

Answer-2
(i) a, b and x
(ii) d, m, n, s, and t.
Question- 3.
In the given figure, figure out the number of angles formed within the arms OA and OE.

Answer-3
∠AOE, ∠AOD, ∠AOC, ∠AOB, ∠BOC ∠BOD, ∠BOE, ∠COD, ∠COE and ∠DOE
Question- 4.
Add :
(i) 29° 16′ 23″ and 8° 27′ 12″
(ii) 9° 45’56” and 73° 8′ 15″
(m) 56° 38′ and 27° 42’30”
(iv) 47° and 61° 17’4″
Answer-4
(i) 29° 16′ 23″ and 8° 27′ 12″
29° 16′ 23″
+ 8° 27′ 12″
37° 43′ 35”
(ii) 9° 45’56” and 73° 8′ 15″
9° 45’56”
+ 73° 8′ 15″
82° 53′ 71″
Since, 60” = 1′ ∴ 71” = 1′ 11”
and ∴ 82° 53′ 71″ = 82° 54′ 11″
(iii) 56° 38′ and 27° 42’30”
56° 38′ + 27° 42’30”
= 84° 20’ 30” ….(1° = 60′)
56° 38′ 0”
+ 27° 42’30”
84° 80’ 30”
20′
(iv) 47° and 61° 17’4″
47° 0′ 0”
+ 61° 17’ 4”
108° 17′ 4”
Question -5.
In the figure, given below name :
(i) three pairs of adjacent angles.
(ii) two acute angles,
(iii) two obtuse angles
(iv) two reflex angles.

Answer-5
(i) Three pairs of adjacent angles are
∠AOB and ∠BOC;
∠BOC and ∠COD;
∠COD and ∠DOA.
(ii) Two acute angles are
∠AOB and ∠AOD.
(iii) Two obtuse angles are
∠BOC and ∠COD.
(iv) Two reflex angles are
∠AOB and ∠COD.
Question- 6.
In the given figure ; PQR is a straight line. If :
(i) ∠SQR = 75° ; find ∠PQS.
(ii) ∠PQS = 110°; find ∠RQS

Answer-6
(i) From figure,
∠PQS + ∠SQR = 180° [Linear pair of angles]
⇒∠PQS + 75° = 180°
⇒ ∠PQS = 180°-75°
⇒ ∠PQS = 105°
(ii) From figure again,
∠PQS + ∠RQS = 180°
⇒ 110° + ∠RQS = 180°
∠RQS = 180°- 110°
∠RQS = 70°
Question -7.
In the given figure ; AOC-is a straight line. If angle AOB = 50°, angle AOE = 90° and angle COD = 25° ; find the measure of :
(i) angle BOC
(ii) angle EOD
(iii) obtuse angle BOD
(iv) reflex angle BOD
(v) reflex angle COE.

Answer-7
(i) ∠AOB + ∠BOC = 180° (Linear pairs of angle)
⇒ 50° +∠BOC = 180°
⇒ ∠BOC = 180° – 50° = 130°
⇒ ∠BOC = 130°
(ii) ∠EOD + ∠COD = 90° (∵AOE = 90°)
⇒ ∠EOD + 25° = 90°
⇒ ∠EOD + 25° = 90°
⇒ ∠EOD = 90° – 25°
⇒ ∠EOD = 65°
(iii) ∠BOD = ∠BOC + COD
= 130° + 25° = 155°
(iv) Reflex ∠BOD = 360° – ∠BOD
= 360°- 155° = 205°
(v) Reflex ∠COE = 360° – ∠COE
= 360° (∠COD + ∠EOD)
= 360° – (25° + 65°)
= 360° – 90° = 270°
Question- 8.
In the given figure if :
(i) a = 130° ; find b.
(ii) b = 200 ; find a.
(iii) a = 5/3 right angle, find b

Answer-8
(i) From figure, a + b = 360°
⇒ 130° + 6 = 360
⇒ 6 = 360°-130°
⇒ b = 230°
(ii) From figure,
a + b = 360°
⇒ a + 200° = 360°
⇒ a = 360° – 200°
⇒ a = 160°
(iii) Here, a= 5⁄3 right angle
= 5⁄3 x90° = 150°
a = 150°
Here, a + b = 360°
⇒ 150° + b = 360° (∵a = 150°)
⇒ b = 360° -150°
b = 210°
Question -9.
In the given diagram, ABC is a straight line.
(i) If x = 53°, find y.
(ii) If y =11⁄2 right angles ; find x.

Answer-9
(i) From the figure,
∠ABD + ∠DBC = 180° (Linear pair of angles)
⇒ x+y=180°
⇒ 53°+y = 180° (∵ x = 53”)
⇒ y = 180° – 53°
⇒ y = 127°
(ii) From figure again,
x+y= 180°
1 + 3⁄2 x 90 = 180°
⇒ x+11⁄2 right angles = 180°
⇒ x+3⁄2 x90=180°
⇒ x + 135°= 180°
⇒ x= 180° – 135°
⇒ x = 45°
Question -10.
In the given figure, AOB is a straight line. Find the value ofx and also answer each of the following :
(i) ∠AOP = ……..
(ii) ∠BOP = ……..
(iii) which angle is obtuse ?
(iv) which angle is acute ?

Answer-10
∠AOP = x + 30°
∠BOP = x – 30°
But ∠AOP + ∠BOP = 180° (∵ ∠AOB is a straight angle)
⇒ x + 30°+x-30° = 180°
⇒ 2x = 180°
⇒ x = 90°
(i) ∠AOP = x + 30° = 90° + 30° = 120°
(ii) ∠BOP = x- 30° = 90° – 30° = 60°
(iii) ∠AOP is an obtuse angle
(iv) ∠BOP is an acute angle
Question- 11.
In the given figure, PQR is a straight line. Find x. Then complete the following:
(i) ∠AQB = ……..
(ii) ∠BQP = ……..
(iii) ∠AQR = …….

Answer-11
PQR is a straight line
∠AQP=x + 20°
∠AQB = 2x + 10°
∠BQR = x – 10°
But ∠AQP + ∠AQB + ∠BQR = 180°
⇒ x + 20° + 2x + 10° + x-10°= 180°
⇒ 4x + 20°= 180°
⇒4x= 180°-20°= 160°
⇒ x = 160⁄4 = 40°
(i) ∠AQB = 2x + 10° = 2 x 40° + 10° = 80° + 10° = 90°
∠AQP = x + 2(T = 40° + 20° = 60°
∠BQR = x – 10° = 40° – 10° = 30°
(ii) ∠BQP = ∠AQP + ∠AQB = 60° + 90° = 150°
(iii) ∠AQR = ∠AQB + ∠BQR = 90° + 30° = 120°
Question- 12.
In the given figure, lines AB and CD intersect at point O.
(i) Find the value of ∠a.
(ii) Name all the pairs of vertically opposite angles.
(iii) Name all the pairs of adjacent angles.
(iv) Name all the reflex angles formed and write the measure of each.

Answer-12
Two lines AB and CD intersect each other at O
∠AOC = 68°
(i) ∵ AOB is a line
∠AOC + ∠BOC = 180°
⇒ 68° + a = 180°
⇒ a= 180°-68° = 112°
(ii) ∠AOC and ∠BOD and ∠BOC and ∠AOD are the two pairs of vertically opposite angles .
(iii) ∠AOC and ∠BOC; ∠BOC and ∠BOD; ∠BOD and ∠DOA;
∠DOA and AOC are the pairs of adjacent angles
(iv) ∠BOC and ∠DOA are reflex angles and also ∠AOC and ∠BOD are also reflex angles
Ref. ∠BOC = 180° + 68° = 248°
Ref. ∠DOA = 180° + 68° = 248°
Ref. ∠AOC = 180° + 112° = 292°
and ref. ∠BOD =180° + 112° = 292°
Question- 13.
In the given figure :
(i) If ∠AOB = 45°, ∠BOC = 30° and ∠AOD= 110°;
find : angles COD and BOD.
(ii) If ∠BOC = ∠DOC = 34° and ∠AOD = 120° ;
find : angle AOB and angle AOC.
(iii) If ∠AOB = ∠BOC = ∠COD = 38°
find : reflex angle AOC and reflex angle AOD.

Answer-13
(i) ∠COD = ∠AOD – ∠AOC
= ∠AOD – (∠AOB + ∠BOC)
= 110°-(45°+ 30°)
= 110°-75° = 35°
∠BOD = ∠AOD -∠AOB
= 110° -45°
= 65°
(ii) ∠AOB = ∠AOD-∠BOD
= ∠AOD – (∠BOC + ∠COD)
= 120° – (34° + 34°)
= 120°-68°
= 52°
∠AOC = ∠AOB + ∠BOC
= 52° + 34°
= 86°
(iii) Reflex ∠AOC = 360°-∠AOC
= 360° – (∠AOB + ∠BOC)
= 360° – (38° + 38°)
= 360° – 76° = 284°
Reflex ∠AOD = 360° – ∠AOD
= 360° (∠AOB + ∠BOC + ∠COD)
= 360° – (38° + 38° + 38°)
= 360°- 114°
= 246°
ICSE Class-6th Concise Mathematics Selina Solutions Exercise – 24 B Angles (With their Types)
Question- 1.
Write the complement angle of :
(i) 45°
(ii) x°
(iii) (x – 10)°
(iv) 20° + y°
Answer-1
(i) Complement angle of 45°
= 90° – 45° = 45°
(ii) Complement angle of x°
= 90° – x° = (90 – x)°
(iii) Complement angle of (x – 10)° = 90° (x – 10°)
= 90°-x + 10° = 100°-x
(iv) Complement angle of 20° + y°
= 90°-(20°+y°)
= 90° – 20° -y° = 70° -y°
Question -2.
Write the supplement angle of :
(i) 49°
(ii) 111°
(iii) (x – 30)°
(iv) 20° + y°
Answer-2
(i) Supplement angle of 49°
= 180°-49° = 131°
(ii) Supplement angle of 111°
= 180°- 1110 = 69°
(iii) Supplement of (x – 30)° = 180° – ( x° – 30°)
= 180o – x° + 30° – 210° – x°
(iv) Supplement of ∠20° + y° = 180° – (20° +y°)
= 180° -20°-y°
= 160° -y°
Question- 3.
Write the complement angle of :

![]()
Answer-3
(i) Complement angle of 1⁄2 of 60°
= 90° – (1⁄2 of 60∘)
= 90° – 30°
= 60°
(ii) Complement angle of 1⁄5 of 160°
= 90° – (1⁄5 × 160∘)
= 90° – 32°
= 58°
(iii) Complement angle of 2⁄5 of 70°
= 90° – (2⁄5 × 70∘)
= 90° – 28°
= 62°
(iv) Complement angle of 1⁄6 of 90°
= 90° – (1⁄6 × 90∘)
= 90° – 15°
= 75°
Question- 4.
Write the Supplement angle of :

Answer-4
(i) Supplement angle of 50% of 120°
= 180° – (50% of 120°)
= 180° – (120°×50⁄100)
= 180° – 60°
= 120°
(ii) Supplement angle of (1⁄3 of 150∘)
= 180° – (1⁄3 of 150°)
= 180° – 50°
= 130°
(iii) Supplement angle of 60% of 100°
= 180° – (60% of 100°)
= 180° – (60⁄100 ×100)
= 180° – 60°
= 120°
(iv) Supplement angle of 3⁄4 of 160°
= 180° – (3⁄4 of 160°)
= 180° – 120°
= 60°
Question -5.
Find the angle :
(i) that is equal to its complement ?
(ii) that is equal to its supplement ?
Answer-5
(i) that is equal to its complement
Let angle be x
and complements is also x
angle + its complement = 90
x + x =90
2x = 90
x = 90⁄2
x = 45
Hence 45° is equal to its complement.
(ii) that is equal to its supplement
Let angle be x
and supplement is also x
angle + its supplement = 180
x + x =180
2x = 180
x = 180⁄2
x = 90
Hence 90° is equal to its supplement.
Question -6.
Two complementary angles are in the ratio 7 : 8. Find the angles.
Answer-6
Let two complementary angles are 7x and 8x
∴ 7x + 8x = 90°
⇒ 15x = 90°
⇒ x = 90⁄15
⇒ x = 6°
∴ Two complementary angles are
7x = 7 x 6° = 42°
8x = 8 x 6° = 48°
Question -7.
Two supplementary angles are in the ratio 7 : 11. Find the angles.
Answer-7
Let two supplementary angles are 7x and 11x
∴ 7x+ 11x= 180°
⇒ 18x = 180°
⇒ x =180⁄18
⇒ x = 10°
Two supplementary angles are
7x = 7 x 10° = 70°
11x= 11 x 10°= 110°
Question- 8.
The measures of two complementary angles are (2x – 7)° and (x + 4)°. Find x.
Answer-8
We know that, sum of two complementary angles = 90°
∴(2x – 7) + (x + 4) = 90°
2x – 7 + x + 4 = 90°
⇒ 2x + x – 7 + 4 = 90°
⇒ 3x – 3 = 90°
⇒ 3x = 90 + 3
⇒ 3x = 93
⇒ x = 93⁄3
x = 31
Question- 9.
The measures of two supplementary angles are (3x + 15)° and (2x + 5)°. Find x.
Answer-9
We know that, sum of two supplementary angles = 180°
∴ (3x + 15)° + (2x + 5)° = 180° ‘
3x + 15 + 2x + 5 = 180°
⇒ 3x + 2x+15 + 5 = 180°
⇒ 5x°+ 20° = 180°
⇒ 5x = 180° – 20°
⇒ 5x= 160°
⇒ x = 160⁄5
⇒ x = 32°
Question- 10.
For an angle x°, find :
(i) the complementary angle
(ii) the supplementary angle
(iii) the value of x° if its supplementary angle is three times its complementary angle.
Answer-10
For an angle x,
(i) Complementary angle of x° = (90° – x)
(ii) Supplementary angle of x° = (180° – x)
(iii) ∵‘Supplementary angle = 3 (complementary anlge)
180° – x = 3 (90°- x)
⇒ 180°- x = 270°- 3x
⇒-x + 3x = 270°- 180°
⇒ 2x = 90°
⇒ x = 90⁄2 = 45°
∴ x = 45°
Revision Exercise Chapter-24 Angles (With their Types) for ICSE Class-6th Concise Selina Mathematics Solutions
Question -1.
Explain what do you understand by :
(i) Adjacent angles ?
(ii) Complementary angles ?
(iii) Supplementary angles ?
Answer-1
(i) Adjacent Angles: Two angles are called adjacent angles if (a) they have a common vertex (b) they have one common arm and (iii) the other two arms of the angles are on the opposite sides of the common arm.
(ii) Complementary Angles : Two angles whose sum is 90° are called complementary angles to each other.
(iii) Supplementary Angles : Two angles whose sum.is 180° are called supplementary angles to each other.
Question- 2.
Find the value of ‘x’ for each of the following figures :


Answer-2:
(i) In given figure, BOC is a straight line
∴ ∠AOC + ∠AOB = 180°
⇒ 75° + 5x + 20° = 180°
⇒ 5x + 95° = 180°
⇒ 5x = 180° – 95° = 85°
⇒ x = 85⁄5 =17∘
∴ x = 17°
(ii)
In given figure, angles are on a point
∴ The sum = 360°
⇒ 75° + 2x + 65° + 3x + x = 360°
⇒ 6x + 140° = 360°
⇒ 6x = 360° – 140° = 220°
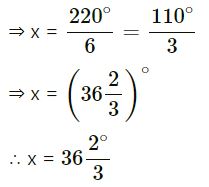
(iii) In given figure, angles are on a point
∴ Their sum = 360°
⇒ 5x + 3x + 40°+ 120° = 360°
⇒ 8x + 160° = 360°
⇒ 8x = 360° – 160° = 200°
⇒ x = 200⁄8=25∘
⇒ x = 25°
Question -3.
Find the number of degrees in an angle that is (i) of a right angle (ii) 0.2 times of a straight line angle.
Answer-3
(i) 3⁄5 of a right angle
=3⁄5×90∘ (∵ 1 right angle = 90°)
= 3 × 18° = 54°
(ii) 0.2 times of a straight line angle
= 0.2 of 180° (Straight line angle = 180°)
=2⁄10×280∘=36∘
Question- 4.
In the given figure; AB, CD and EF are straight lines. Name the pair of angles forming :
(i) straight line angles.
(ii) vertically opposite angles.

Answer-4
(i)In the given figure, AB, CD and EF are straight lines on intersecting, angles are formed a, b, c, d, l, m, n and p.
In the figure pairs of straight-line angles are ∠a, ∠b; ∠b, ∠c; ∠c, ∠d; ∠d, ∠a ∠l, ∠m; ∠m, ∠n;∠n, ∠p and ∠p, ∠l.
(ii) In the given figure, AB, CD and EF are straight lines on intersecting, angles are formed a, b, c, d, l, m, n and p.
Pairs of vertically angles are ∠a, ∠c; ∠b, ∠d; ∠l, ∠n; ∠m, ∠p.
Question- 5.
Find the complement of :

Answer- 5
(i) We know that two angles are called complementary when their sum is 90°. Now
2⁄5 of 210∘
=2⁄5×210∘=2×42∘=84∘
∴ Its complement will be = 90° – 84° = 6°
(ii) We know that two angles are called complementary when their sum is 90°. Now
0.4 times of 130° = 4⁄10×130∘
= 4 × 13° = 52°
∴ Its complement will be = 90° – 52° = 38°
Question- 6.
Find the supplement of :

Answer-6
(i) We know that two supplementary angles are those whose sum is 180°. Now
5⁄7 of 154°
=5⁄7×154°=5×22°=110°
∴ Its supplement = 180° – 110° = 70°
(ii) We know that two supplementary angles are those whose sum is 180°. Now
0.7 times of 150°
=7⁄10×150°=7×15°=105°
∴ Its supplement = 180° – 105° = 75°
Question -7.
Two complementary angles are in the ratio 8 : 7. Find the angles.
Answer-7
Let two complementary angles are 7x and 8x
∴ 7x + 8x = 90°
⇒ 15x = 90°
⇒ x = 90⁄15
⇒ x = 6°
∴ Two complementary angles are
7x = 7 x 6° = 42°
8x = 8 x 6° = 48°
Question- 8.
Two supplementary angles are in the ratio 7 : 5. Find the angles.
Answer-8
Ratio between two supplementary angles are 7 : 5
∴ Sum of ratios = 7 + 5 = 12
But sum of two supplementary angles = 180°
∴ First angle = 180∘×7⁄12=15∘×7=105∘
and second angle = 180∘×5⁄12=15∘×5=75∘
∴ Two supplementary angles are 105° and 75°
Question- 9.
Two supplementary angles are (5x – 82°) and (4x + 73°). Find the value of x.
Answer-9
∵ Sum of two supplementary angles = 180°
∴ (5x – 82°) + (4x + 73°) = 180°
5x – 82° + 4x + 73° = 180°
9x – 9° = 180°
9x = 180° + 9° = 189°
x = 189⁄9=21°
∴ x = 21°
Question -10.
Find the angle formed by the arms of a clock at:
(i) 3 O’clock
(ii) 6 O’clock
(iii) 9 O’clock
(iv) 12 O’clock
Answer-10
(i) 3 O’clock
We know that sum of angles at a point = 360
and on the face of a clock there are 12 marks on it.
Now at 3 O’clock, the hour hand is on 3 while minute hand is at 12
∴ Angle between them =3⁄12×360∘
= 3 × 30° = 90°
(ii) 6 O’clock
We know that sum of angles at a point = 360° and on the face of a clock there are 12 marks on it.
Now at 6 O’clock, the hour hand is on 6 while minute hand is at 12
∴ Angle between them = 6⁄12×360∘
= 6 × 30° = 90°
(iii) 9 O’clock
We know that sum of angles at a point = 360° and on the face of a clock there are 12 marks on it.
Now at 9 O’clock, the hour hand is on 9 while minute hand is at 12
∴ Angle between them 9⁄12×360∘
= 9 × 30° = 270°
(iv) 12 O’clock
We know that sum of angles at a point = 360° and on the face of a clock there are 12 marks on it.
Now at 12 O’clock, the hour hand and minute hand are both 12°
∴ Angle between them =12⁄12×360∘=360° or 0° as both hands coincide each other.
Question – 11.
For an angle y°, find :
(i) its supplementary angle.
(ii) its complementary angle.
(iii) the value of y° if its supplement is four times its complement.
Answer-11
(i) Its supplementary angle = 180° – y
(ii) Its complementary angle = 90° – y
(iii) ∴ supplementary angle of y = 4 …(complementary angle of y)
∴ 180° – y = 4 (90° – y)
⇒ 180° – y = 360° – 4y
⇒ 4y – y = 360° – 180°
⇒ 3y = 180°
⇒ y = 180⁄3=60∘
∴ y = 60°
Question- 12.
Use the adjoining figure to find :
(i) ∠BOD
(ii) ∠AOC
Answer-12
(i) ∠BOD
But sum of angles on the same side of a line = 180°
∴ ∠AOD + ∠COD + ∠BOC = 180°
72° + ∠COD + 64° = 180°
∠COD = 180° – (72° + 64°)
= 180° – 136° = 44°
(i) Now ∠BOD = ∠BOC + ∠COD
= 64° + 44° = 108°
(ii) ∠AOC = ∠AOD + ∠COD
= 72° + 44° = 116°
Question- 13.
Two adjacent angles forming a linear pair are in the ratio 7:5, find the angles.
Answer-13
In the given figure, ∠AOC and ∠BOC are adjacent angles which form a linear pair
∴ ∠AOC ∠BOC = 180°
But ∠AOC : ∠BOC = 7 : 5
Let ∠AOC = 7x and ∠BOC = 5x
∴ 7x + 5x = 180°
⇒ 12x = 180°
⇒ x = 180⁄12 =15∘
∴ ∠AOC = 7x = 7 × 15 = 105°
and ∠BOC = 5x = 5 × 15 = 75°
Question- 14.
Find the angle that is three times its complementary angle.
Answer-14
Let given angle = x
Let complementary angle of a given angle is y
∴ then x + y = 90
But x = 3y
∴ 3y + y = 90°
⇒ 4y = 90°
⇒ y = 90⁄4 = 22.5°
∴ complementary = x = 90° – 22 – 5° = 67.5°
Question- 15.
An angle is one-thirds of a straight line angle ; find :
(i) the angle
(ii) the complement and the supplement of the angle obtained above.
Answer-15
straight angle = 180°
∴ given angle = 1⁄3×180∘ = 60°
(i) complement of the given angle
= 90° – 60° = 30°
(ii) Supplement of the given angle
= 180° – 60° = 120°
End of Angles ICSE Class-6th Concise Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -6
Thanks


