Area of Plane Figures Class 9 OP Malhotra Exe-16A ICSE Maths Solutions Ch-16. We Provide Step by Step Solutions / Answer of Questions of OP Malhotra Maths. Visit official Website CISCE for detail information about ICSE Board Class-9 Mathematics.

Area of Plane Figures Class 9 OP Malhotra Exe-16A ICSE Maths Solutions Ch-16
| Board | ICSE |
| Publications | S Chand |
| Subject | Maths |
| Class | 9th |
| Chapter-16 | Area of Plane Figures |
| Writer | OP Malhotra |
| Exe-16A | Solved Problems on Rectangle / Squire |
| Edition | 2025-2026 |
Solved Problems on Rectangle / Squire
Area of Plane Figures Class 9 OP Malhotra Exe-16A ICSE Maths Solutions Ch-16
Que-1: Find the perimeter and area of the rectangle whose dimensions are
(i) 8 cm by 5 cm
(ii) 12 m by 9 m
(iii) 3.5 cm by 2 m
Sol: (i) Length of rectangle (l) = 8 cm
Breadth (b) = 5 cm
∴ Perimeter = 2 (l + b) = 2 (8 + 5) cm
= 2 × 13 = 26 cm
and area = l × b = 8 × 5 = 40 cm2
(ii) Length of rectangle (l) = 12 m
and breadth (b) = 9 m
∴ Perimeter = 2 (l + b) = 2 (12 + 9) m
= 2 × 21 = 42 m
and area = l × b = 12 × 9 = 108 m2
(iii) Length of the rectangle (l) = 3.5 m
and breadth (b) = 2 m
∴ Perimeter = 2 (l + b) = 2(3.5 + 2) m
= 2 × 5.5 = 11 m
and area = l × b = 3.5 × 2 m2
= 7 m2
Que-2: Find the perimeter and area of the square whose each side is
(i) 3 cm
(ii) 5 m
(iii) 1.3 m
(iv) 2.4 m
Sol: (i) Side of the square (a) = 3 cm
∴ Perimeter = 4a = 4 × 3 = 12 cm
and area = a2 = (3)2 = 9 cm2
(ii) Side of the square (a) = 5 m
∴ Perimeter = 4a = 4 × 5 = 20 m
and area = a2 = (5)2
= 25 m2
(iii) Side of square (a) = 1.3 m
∴ Perimeter = 4a = 4 × 1.3 m
= 5.2 m
and area = a2 = (1.3)2 m2
= 1.69 m2
(iv) Side of the square (a) = 2.4 m
∴ Perimeter = 4a = 4 × 2.4 = 9.6 m
and area = a2 = (2.4)2 m2
= 5.76 m²
Que-3: Find the length of one side and perimeter of a square whose area is :
(a) 25 m2
(b) 144 m2
(c) 256 cm2
(d) 961 dm²
Sol: (i) Area of the square = 25 m²
∴ Side of square (d) = √Area = √25 = 5 m
∴ Perimeter = 4a = 4 × 5 m = 20 m
(ii) Area of the square = 144 m²
∴ Side (a) = √Area = √144 m = 12 m
and perimeter = 4a = 4 × 12 = 48 m
(iii) Area of the square = 256 cm²
∴ Side (a) = √Area = √256 = 16 cm
and perimeter = 4 a = 4 × 16 = 64 cm
(iv) Area of the square = 961 dm²
∴ Side (a) = Area√ = √961 = 31 cm
and perimeter = 4a = 4 × 31 = 124 cm
Que-4: The perimeter of a rectangle is 30 cm, and its breadth is 6 cm, find its length and its area.
Sol: Perimeter of a rectangle = 30 cm
and breadth (b) = 6 cm
∴ l + b = Perimeter / 2 = 30/5 = 15 cm
∴ Length = 15 – 6 = 9 cm
and area = l × b = 9 × 6 = 54 cm²
Que-5: The area of a rectangular courtyard, 30 m long, is 450 m2. Find its breadth and perimeter.
Sol: Area of rectangular compound = 450 m2 Length (l) = 30 m
∴Breadth = Area / Length = 450/30 = 15 cm
and perimeter = 2 (l + b)
= 2 (30 + 15) m
= 2 × 45 = 90 m
Que-6: The perimeter of a rectangular field is 3/5 km. If the length of the field is twice its width, find its area in sq. metres.
Sol: Perimeter of a rectangular field = 35 km
= (3/5) × 1000 = 600 m
Let width of the field = x m
Then length = 2 x m
Now l + b = Perimeter / 2 = 600/2 = 300 m
∴ 2x + x = 300 ⇒ 3x = 300
⇒ x = 300/3 = 100
∴ Length (l) = 2x = 2 × 100 = 200 m
and breadth (b) x = 100 m
and area = l × b = 200 × 100 = 20000 m²
Que-7: If the side of a square is doubled, find the ratio of the area of the resulting square to that of the given square.
Sol: Let side of square = a m
Then area = (side)2 = a2 m2
If the side is doubled, then
Side = 2a
and area = (side)2
= (2a)2 = 4a2
∴ Ratio in the two area = 4 a2 : a2 = 4 : 1
Que-8: The side of a square field is 89 m. By how many square metres does its area fall short of a hectare ?
Sol: Side of a square field (a) = 89 m
Area = a2 = (89)2 m2 = 7921 m2
∴ Difference between 1 hectare and 7921 m2
= 10000 – 7921 (1 hectare = 10000 m2)
= 2079 m²
Que-9: The side of a square is 25 cm. Find the length of its diagonal correct to 2 decimal places.
Sol: Side of a square (a) = 25 cm
∴ Length of its diagonal = √2 a
= 1.414 × 25 cm
= 35.350 = 3535 cm
Que-10: If the diagonal of a rectangle is 10 cm and its width is 6 cm, find its area.
Sol: Diagonal of rectangle = 10 cm
and breadth (b) = 6 cm
∴ (Diagonal)2 = l2+ b2
⇒ (10)2 = (6)2 + l2
⇒ 100 = 36 + l2 ⇒ l2 = 100 – 36 = 64
⇒ l2 = 64 = (8)2
∴ l = 8
∴ Length = 8 cm
Now area = l × b = 8 × 6 = 48 cm²
Que-11: The length of a rectangle is twice its width. If the length of its diagonal is 16√5 cm, find its area.
Sol: Length of a diagonal of a rectangle = 16√5 cm
Let breadth (b) = x cm
Then length (l) = 2x cm
∴ (Diagonal)² = l² + b²
(16√5)² = (2x)² + x²
256 × 5 = 4x² + x² ⇒ 5x² = 256 × 5
⇒ x² = (256×5)/5 = 256 = (16)²
∴ x = 16
∴ Length (l) = 2x = 2 × 16 = 32 cm
and breadth = x = 16 cm
and area = l × b
= 32 × 16 cm² = 512 cm²
Que-12: The sides of two squares are in the ratio 2 : 3 . Find the ratio of their perimeters and areas.
Sol: Ratio in the sides of two squares = 2 : 3
Let side of the first square (a) = 2x
and of second (A) = 3x
Now perimeter of the first square = 4a
= 4 × 2x = 8x
and that of the second square = 4 × 3x = 12x
∴ Ratio in their perimeter = 8x : 12x
=2 : 3
(ii) Area of the first square (a)2 = (2x)2 = 4x2
and area of the second square (A)2 = (3x)2 = 9x2
and ratio between their areas = 4x2 : 9x2 = 4 : 9
Que-13: How many carpets, 3 m by 2 m, are required to cover the floor of a hall 30 m by 12 m ?
Sol: Length of the floor (L) = 30 m and breadth (B) = 12 m
∴ Area of floor = L × B = 30 × 12 = 360 m2
Now length of carpet (l) = 3 m
and breadth (b) = 2m
∴ Area of one carpet = l × b = 3 × 2 = 6 m²
∴ No. of carpets = Area of floor / Area of one carpet
= 360/6 = 60 carpets
Que-14: A room is 5 m by 4 m. Find the cost of cementing its floor at Rs. 7.50 per m2.
Sol: Length of a room (l) = 5 m and breadth (b) = 4 m
∴ Area = l × b = 5 × 4 = 20 m2
Cost of cementing per m2 = Rs. 7.50
Total cost = Rs.7.50 × 20 = Rs.150.00
= Rs. 150
Que-15: A room is 12 m by 10 m by 10 m. Find the cost of covering its floor with bricks 20 cm by 6 cm, if the cost of one thousand bricks is Rs. 300.
Sol: Length of a room (l) = 12 m
Breadth (b) = 10 m
and height (h) = 10 m
∴ Area of floor = l × b = 12 × 10 = 120 m²
Length of one brick = 20 cm
and breadth = 6 cm
∴ Area of one brick = 20 × 6 = 120 cm²
= 120/(100 × 100) = 12/1000 cm²
No. of bricks required = Area of floor / Area of one brick
= (120/12) × 1000 = 10000 bricks
Que-16: In exchange for a square plot of land, one of whose sides is 84 m, a man wants to buy a rectangular plot 144 m long and of the same area as the square plot. Determine the width of the rectangular plot.
Sol: Side of the square field (a) = 84 m
∴ Area = a² = (84)² m²
= 84 × 84 = 7056 m²
∴ Area of rectangular field = 7056 m²
Length of the field (l) = 144 m
∴ Breadth = Area / Length = 7056/144 m = 49 m
Que-17: A plot 110 metres long and 80 metres broad is to be covered with grass leaving 5 metres all around. Find the area to be laid with grass.
Sol: Length of plot (l) = 110 m and breadth (b) = 80 m

Area of the plot = l × b
= 110 × 80 = 8800 m2
Leaving 5 m all around, then
Length of inner part = 110 – 2 × 5
= 110 – 10 = 100 m
and inner breadth = 80 – 2 × 5 = 80 – 10 = 70 m
∴ Inner area where grass is laid
=100 × 70 = 7000 m²
Que-18: The dimensions of a rectangular field are in the ratio 6 : 5. Find the cost of constructing a fence around the field at the rate of Rs. 1.25 per metre, given that the area of the field is 27000 m2.
Sol: Ratio in the dimensions of the field = 6 : 5
Let length (l) = 6x m
and breadth (b) = 5x m
∴ Area = l × b = 6x × 5x = 30 x² m²
Now area of the field = 27000 m²
∴ 30×2 = 27000
⇒ x2 = 27000/30 = 900 = (30)²
∴ x = 30
∴Length = 6x = 6 × 30 = 180 m
and breadth = 5x = 5 × 30 = 150 cm
and perimeter = 2(l + b) = 2(180 + 150) m
=2 × 330 = 660 m
Cost of fence = Rs. 1.25 per m
∴ Total cost = Rs. 1.25 × 660 = Rs. 825
Que-19: The cost of enclosing a rectangular garden with a fence all round at the rate of 75 paise per metre is Rs. 300. If the length of the garden is 120 metres, find the area of the garden in square metres.
Sol: Total cost of fencing = Rs. 300
Perimeter of the garden = Rs.30034 m
= (300×4)/3 = 400 m
∴ l + b = Perimeter / 2
= 400/2 = 200 m
Length (l) = 120 m
∴ Breadth (b) = 200 – 120 = 80 m
Now area of the garden = l × b
= 120 × 80 m² = 9600
Que-20: Find the area and perimeter of a square plot of land, the length of whose diagonal is 14 metres. Give your answer correct to 2 places of decimals.
Sol: Diagonal of a square plot = 14 m

Side (a) = Diagonal / √2 = 14 / √2
∴ Area = ( Diagonal )²/2 = (14)²/2 m²
= 196/2 = 98 m²
and perimeter = 4a = (4×14)/√2 m
= (4×14×√2)/(√2×√2) = (4×14×√2)/2 m
= 28√2 = 28(1.4142) m
= 39.5976 = 39.60 m
Que-21: A lawn 10 m by 8 m is surrounded by a path 1 m wide. Find the area of the path.
Sol: Length of lawn (l) = 10 m
and breadth (b) = 8 cm
Width of path = 1 m
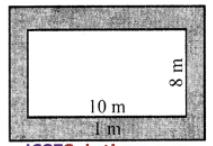
Outer length (L) = 10 + 1 × 2 = 10 + 2 = 12 m
and outer width (B) = 8 + 1 × 2
= 8 + 2 = 10 m
Now area of path = Outer area – Inner area
= L × B – l × b
= 12 × 10 -10 × 8
= 120 – 80 = 40 m²
Que-22: The diagram given below shows two paths drawn inside a rectangular field 50 m long and 35 m wide. Find the area of the shaded portion.

Sol: Length of the rectangular field (l) = 50 m and breadth (b) = 35 m
Width of each path = 5 m
∴ Area of two paths = 50 × 5 + 35 × 5 – (5)2
= 250 + 175 – 25
= 425 – 25 = 400 m2
∴ Area of shaded portion = 400 m²
Que-23: Find the area of the four walls of a room, 7 m long, 5 m broad, and 3 m high. Find the cost of distempering the walls at the rate of Rs. 3.15 per m2.
Sol: Length of room (l) = 7 m
Breadth (b) = 5 m
and height (h) = 3 m
∴ Area of four walls = 2 (l + b) h
= 2 (7 + 5) × 3 = 2 × 12 × 3 m2
= 72 m2
Rate of distempering = Rs. 3.15 per m2
∴ Total cost = Rs. 3.15 × 72 = Rs. 226.80
Que-24: Find the cost of the paper for the walls of the room if each piece of paper is 40 cm wide and 60 cm long : the room is 6 m long, 4 m wide, 3 m high and the cost of paper is Rs. 1.40 per piece; allow 11 m2 for doors, etc., and assume that a whole number of pieces has to be bought.
Sol: Length of room (l) = 6 m = 600 cm
Breadth (b) = 4 m = 400 cm
and height (h) = 3 m = 300 cm
∴ Area of 4-walls = 2 (l + b) × h = 2 (600 + 400) × 300 cm²
= 2 × 1000 × 300 = 600000 cm²
Length of paper = 60 cm
and breadth = 40 cm
∴ Area of 1 paper = 40 × 60 = 2400 cm²
Area of doors etc. = 11 m²
= 11 × 100 × 100 cm² = 110000 cm²
∴ Remaining area = 600000 – 110000 = 490000 cm²
∴ No. of papers required = 490000/2400
= 4900/24 = 204.166 = 205 sheets
Cost of one sheet = Rs. 1.40
∴ Total cost = 205 × Rs.1.40 = Rs. 287
Que-25: A cistern 6 m long, 4 m wide, contains water to a depth of 1 m 25 cm : find the area of the wet surface.
Sol: Length of cistern (l) = 6 m
Breadth (b) = 4 m
Level of water (h) = 1.25 m
Area of wet surface = area of 4 – walls + area of base
=2(6 + 4) × 1.25 + 6 × 4 m2
= 2 × 10 × 1.25 + 24 = 25 + 24 m2 = 49 m²
Que-26: Find the area and perimeter of the shape illustrated in figure given below. The corners are all right angles.

Sol: In the figure by joining the upper portion, we get the rectangles
Length of outer rectangle (l) = 6 + 2 + 2 = 10 cm
and breadth (B) = 5 cm
Length of inner rectangle (l) = 6 cm
and breadth (b) = 3 cm
(i) Area of the given figure = L × B – l × h
= 10 × 5 – 6 × 3
= 50 – 18 = 32 cm2
(ii) Perimeter = (5 + 10 + 5 + 2 + 3 + 6 + 3 + 2) cm = 36 cm
Que-27: Find the area of the figure, in which all corners are right-angles and the dimensions are shown in centimetres.

Sol: In the figure all the dimensions are in cm By joining as shown in the figure we have 3 rectangles
Area of rectangle I = 4*(1/4) × 4 = 17 cm²
Area of rectangle II = 7 × {3*(1/2)} = 7×(7/2)
= 49/2 = 24.5 cm²
Area of rectangle III = 3 × {4*(1/2)} = 3 × (9/2)
= 27/2 = 13.5 cm²
Total area of the figure = 17 + 24.5 + 13.5 cm² = 55 cm²
Que-28: How many tiles, each 12 cm by 6 cm are needed for a floor of a room 162 cm long, 144 cm wide
Sol: Length of the floor of a room = 162 cm
and breadth = 144 cm
∴ Area of floor = length × breadth = 162 × 144 cm²
Now length of one tile =12 cm
Breadth = 6 cm
∴ Area of one tile = 12 × 6 = 72 cm²
∴ No. of tiles required = Area of floor / Area of one tile
= (162×144)/72 = 324 tiles
Que-29: How many dusters, each 16 cm square can be cut from material 84 cm long, 36 cm wide? What areas remains over?
Sol: Length (l) = 84 cm
Breadth (b) = 36 cm
Area = l × b = 84 × 36 cm²
Side of square duster = 16 cm
∴ Area of one duster = 16 × 16 cm²
∴ No. of total duster = Area of total / cloth Area of one duster
= (84×36)/(16×16) = 11.8125
∴ Complete duster to be cut = 11 and remaining cloth
= 84 × 36 = 11 × 256
= (3024 – 2816) cm²
= 208 cm
Que-30: A floor which measure 15 m × 8 m is to be laid with tiles measuring 50 cm × 25 cm. Find the number of tiles required. Further, if a carpet is laid on the floor so that a space of 1 m eixst between its edges and the edges of the floor, what fraction of the floor is uncovered?
Sol: Length of floor (l) = 15 = 1500 cm
Breadth (b) = 8 m = 800 cm
∴ Area of floor = l × b
=1500 × 800 cm² = 1200000 cm²
Area of one tile = 50 cm × 25 cm = 1250 cm²
∴ No. of tiles = Area of floor / Area of one tile
= 1200000/1250 = 960
Space left for carpeting = 1 m
∴ Inner length = 15 – 1 × 2 = 15 – 2 = 13 m
and inner breadth = 8 – 1 × 2 = 8 – 2 = 6 m
Area of the space left uncovered
= outer area – inner area
= 15 × 8 – 13 × 6 = 120 – 78 m2 = 42 m2
∴ Fraction of the floor which is uncovered = 42/120 = 7/20 part
— : End of Area of Plane Figures Class 9 OP Malhotra Exe-16A ICSE Maths Solutions Ch-16. :–
Return to :– OP Malhotra S Chand Solutions for ICSE Class-9 Maths
Thanks
Please Share with Your Friends