Area of Plane Figures Class 9 OP Malhotra Exe-16B ICSE Maths Solutions

Area of Plane Figures Class 9 OP Malhotra Exe-16B ICSE Maths Solutions Ch-16.  We Provide Step by Step Solutions / Answer of Area of Triangle for OP Malhotra Maths. Visit official Website CISCE  for detail information about ICSE Board Class-9 Mathematics.

Area of Plane Figures Class 9 OP Malhotra Exe-16B ICSE Maths Solutions Ch-16

Board	ICSE
Publications	S Chand
Subject	Maths
Class	9th
Chapter-16	Area of Plane Figures
Writer	OP Malhotra
Exe-16B	Solved Questions on Area of Triangle
Edition	2025-2026

Solved Questions on Area of Triangle

Area of Plane Figures Class 9 OP Malhotra Exe-16B ICSE Maths Solutions Ch-16

Que-1: For any triangle, complete the following table.

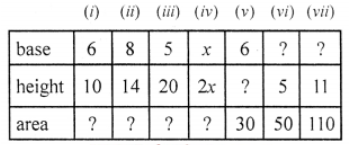
Sol: Area = (1/2) base × height,
base = (Area × 2) / height

Que-2: The area of a triangle is 6 cm² and its base is 4 cm. Find its height.

Sol: Area = 6 cm²
Base = 4 cm
∴ Height = (Area × 2) / base
= (6×2)/4 = 3 cm

Que-3: Find the base of a triangle if its
(i) area is 25 ares and height 20 m.
(ii) area is 16 hectares and height 40 decametres.
1 are = 100 m²
1 hectare = 10000 m²
1 decametre = 10 m

Sol: (i) Area of a triangle = 25 ares
= 25 × 100 = 2500 m²
Height (h) = 20 m
∴ Base = (Area × 2) / height
= (2500×2)/20 = 250 m

(ii) Area of a triangle = 16 hectares
=16 × 10000 m² = 160000 m²
Height = 40 decameter
= 40 × 10 = 400 m
∴ Base = (Area × 2) / height
= (160000×2)/400 = 800 m

Que-4: Find the area of the triangle whose sides are
(i) 26 cm, 28 cm, 30 cm
(ii) 48 cm, 73 cm, 55 cm
(iii) 21 cm, 20 cm, 13 cm
(iv) 7.5 cm, 18 cm, 19.5 cm

Sol: (i) Sides of a triangle
= 26 cm, 28 cm, 30 cm

(ii) 48 cm, 73 cm, 55 cm

(iii) 21 cm, 20 cm, 13 cm

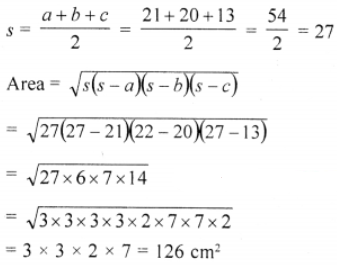
(iv) 7.5 cm, 18 cm, 19.5 cm

Que-5: The perimeter of a triangle is 540 m and its sides are in the ratio 25 : 17 : 12. Find the area of the triangle.

 Sol: Perimeter of a triangle = 540 m
Sides are in the ratio = 25 : 17 : 12
Sum of ratios = 25 + 17 + 12 = 54
∴ First side (a) = (540×25)/54 = 250 m
Second side (b) = (540×17)/54 = 170 m
Third side (c) = (540×12)/54 = 120 m

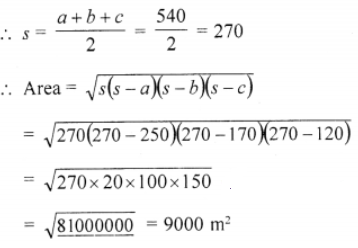
Que-6: The given figure, ABCD represents a square of side 6 cm. F is a point on DC such that the area of the triangle ADF is one-third of the area of the square. Find the length of FD.

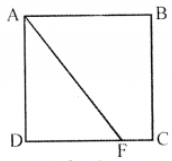
Sol: In square ABCD,
F is a point on DC. AF is joined
Side of square = 6 cm
∴ Area of square ABCD = (side)²
= (6)² = 36 cm²
Then area of right △ADF
= 13 × 36 = 12 cm²
Height AD = 6 cm
Base DF = (Area × 2) / Height
= (12×2)/6 = 4 cm
Hence FD = 4 cm.

Que-7: Find the area of a triangle with base 5 cm and whose height is equal to that of a rectangle with base 5 cm and area 20 cm².

Sol: Area of a rectangle = 20 cm² Base (l) = 5 cm
∴ Height (b) = Area Base = 205 = 4 cm
∴ Height of the triangle = 4 cm
and base = 5 cm
∴ Area = 12 Base × Height
= 12 × 5 × 4 = cm²

Que-8: Answer true or false :
(i) The area of a triangle with base 4 cm and perp. height 6 cm is 24 cm2.
(ii) The area of a triangle with sides measuring a, b, c, is given by √{s(s−a)(s−b)(s−c)} where s is the perimeter of the triangle.
(iii) The area of a rectangle and a triangle are equal if they stand on the same base and are between the same parallels.

Sol: (i) Area of triangle = (1/2) base × height
= (1/2) × 4 × 6 = 12 cm²
∴ Area = 24 cm² is false.

(ii) By Hero’s formula
Area = √{s(s−a)(s−b)(s−c)}
When s = (a+b+c)/2 i.e. half perimeter
But s is the perimeter as given
∴ It is false.

(iii) It is also false.
∵ If a rectangle and a triangle are on the same base and between the same parallels, then area of triangle = (1/2) the area of rectangle.

Que-9: ABC is a triangle in which AB = AC = 4 cm and ∠A = 90°. Calculate the area of △ABC.

Sol: In △ABC, ∠A = 90°
AB = AC = 4 cm

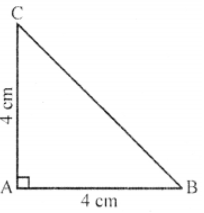
Area = (1/2) base × height
= (1/2) × AB × AC
= (1/2) × 4 × 4 = 8 cm²

Que-10: The sides of a triangular field are 320 m, 200 m and 180 m long. Using ruler and compasses only, draw the plan of the field using the scale 50 m = 1 cm. Construct the altitude of the triangle on the side representing 320 m. Measure the altitude and use your result to calculate the area of the actual field in m².

Sol: The sides of a triangle are 320 m, 200 m, 180 m
Taking 50 m = 1 cm
Then the sides will be
BC = 320/50 = 6.4 cm, AB = 200/50 = 4 cm
and AC = 180050 = 3.6 cm

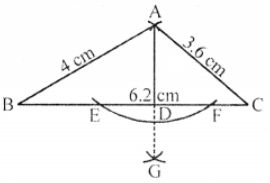
Steps of construction :
(i) Draw a line segment BC = 6.4 cm.
(ii) With centre B and radius 4 cm, draw an arc.
(iii) With centre C and radius 3.6 cm draw another arc which intersects the first arc at A.
(iv) Join AB and AC.
△ABC is the required triangle
(v) With centre A and a suitable radius, draw an arc which intersects BC at E and F.
(vi) With centers E and F and radius more than half of EF, draw two arcs below BC, intersecting each other at G.
(vii) Join AG which intersect BC at D. Then AD is the altitude on BC.
On measuring its length it is 2.05 cm (approx) or 102.5 m
Area of △ABC = (1/2) BC × AD
= (1/2) × 320 × 102.5 m2
= 16400.0 m²
= 16400 m² (approx)

Que-11: The sides of a triangular field are 975 m, 1050 m and 1125 m. If this field is sold at the rate of Rs. 1000 per hectare, find its selling price.

Sol: Let the sides of a Δ are
α = 915 m, b = 1050 m, c = 1125 m
∴ s = (a+b+c)/2 = (975+1050+1125)/2 = 3150/2 = 1575

Que-12: Find the area of the equilateral triangle whose each side is (a) 12 cm (b) 5 cm.

Sol: (a) Side of equilateral Δ (a) = 12 cm
∴ Area of equilateral Δ = (√3/4) a²
= (√3/4) (12)² cm²
= (√3/4) × 144 cm²
= 36 × 1.732 cm³ = 62.352 cm²

(b) Side of the equilateral Δ (a) = 5 cm
∴ Area of the triangle = (√3/4) a²
= (1.732/4) × 5 × 5 cm
= 0.433 × 25 cm³ = 10.825 cm³

Que-13: The perimeter of an equilateral triangle is 24 cm. Find its area.

Sol: Perimeter of an equilateral triangle = 24 cm
∴ Side (a) = Perimeter 3 = 24/3 = 8 cm
and area = (√3/4) a² = (√3/4) × (8)² cm³
= √3 × 16 = 16(1.732) cm³
= 27.712 cm²

Que-14: The perimeter of an equilateral triangle is √3 times its area. Find the length of each side.

Sol: Let length of each side of an equilateral triangle = a
∴ Perimeter = 3a
and area = (√3/4) a²
Now according to the condition,
Perimeter = √3 × area
3a = (√3×√3)/4 a² = 12a = 3a²
⇒ a = 4
∴ Side = 4 units

Que-15: The area of an equilateral triangle is 173.2 m². Find its perimeter.

Sol: Area of equilateral triangle = 173.2 m²

∴ Perimeter = 3a = 3 × 20 m = 60 m

Que-16: Find the area of the isosceles triangle whose
(i) each of the equal sides is 8 cm and the base is 9 cm;
(ii) each of the equal sides is 10 cm and the base is 12 cm;
(iii) each of the equal sides is 7.4 cm and the base is 6.2 cm;
(iv) perimeter is 11 cm and base is 4 cm.

Sol: (i) Each of equal side AB = AC = 8 cm and base BC = 9 cm
Draw AD ⊥ BC which bisects BC at D
∴ BD = DC = 9/2 = 4.5 cm
Now in right △ABD
∴ AB² = AD² + BD² (Pythagoras Theorem)
⇒ AD² = AB² + BD²
= 8² – 4.5² = 64 – 20.25 = 43.75
∴ AD = √43.75 = 6.61 cm
∴ Area = (1/2) base × height
= (1/2) × 9 × 6.614 cm²
= 29.763 = 29.76 cm²

(ii) In △ABC,
AB = AC = 10 cm
BC = 12 cm
AD ⊥ BC is drawn which bisects BC at D
∴BD = DC = 12/2 = 6 cm
Now in right △ABD
AB² = A² + B² (Pythagoras Theorem)
AD² = A² – B²
= (10)² – (6)² =100 – 36 = 64
=(8)²
∴ AD = 8 cm
Now area of △ABC = (1/2) × BC × AD
= (1/2) × 12 × 8 = 48 cm²

(iii) Each equal side AB = AC = 7.4 cm
and base BC = 6.2 cm
AD ⊥ BC is drawn which bisects BC and D
∴ BD = DC = 6.2/2 = 3.1 cm
Now in right △ABD
AB² = AD² + BD² (Pythagoras Theorem)
AD² = AB² – BD²
= (7.4)² -(3.1)² = 54.76 – 9.61 = 45.15
∴ AD = √45.15 = 6.719
∴ Area of △ABC = (1/2) × BC × AD
= (1/2) × 6.2 × 6.719 cm²
= 20.8289 cm² = 20.8 cm²

(iv) Perimeter of an isosceles triangle ABC = 11 cm
and base = 4 cm
∴ AB + AC = 11 – 4 = 7 cm
and AB = AC = 7/2 = 3.5 cm
Draw AD ⊥ BC which bisects BC at D
∴ BD = DC = 4/2 = 2 cm
Now in right △ABD
AB² = AD² + BD² (Pythagoras Theorem)
∴ AD² = AB² – BD² = (3.5)² – (2)²
= 12.25 – 4 = 8.25
∴ AD = √8.25 = 2.872
Now area of △ABC = (1/2) BC × AD
= (1/2) × 4 × 2.872
= 5.744 = 5.74 cm²

Que-17: (i) The base of an isosceles triangle is 24 cm and its area is 192 sq. cm. Find its perimeter.
(ii) Find the base of an isosceles triangle whose area is 12 cm² and one of the equal sides is 5 cm.

Sol: Solution:
(i) Base of an isosceles triangle ABC = 24 cm
and area = 192 cm²

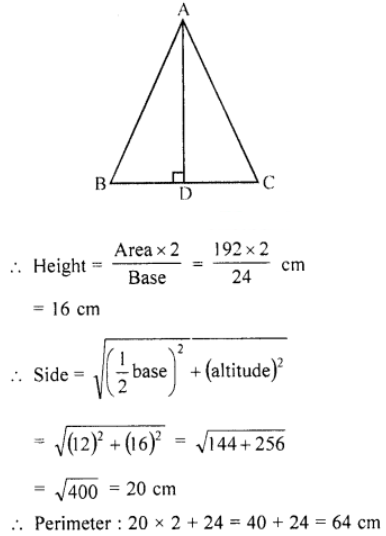
(ii) Area of an isosceles △ABC = 12 cm²
Length of each equal sides
AB = 5 cm
Let AD be perpendicular on base BC and BC = b
∴ BD = DC = b/2

Squaring both side,
b² (100 – b²) = (48)² ⇒ 100 b² – b⁴ = 2304
⇒ b⁴ – 100 b² + 2304 = 0
⇒ b⁴ – 36 b² – 64 b² + 2304 = 0
⇒ b²(b² – 36) – 64(b² – 36) = 0
⇒ (b² – 36) (b² – 64) = 0
Either b² – 36 = 0, then b² = 36 ⇒ b = 6
or b² – 64 = 0 then b² = 64
⇒ b = 8
∴ Base = 8 cm or 6 cm

Que-18: The perimeter of an isosceles triangle is 42 cm. Its base is 2/3 times the sum of equal sides. Find the length of each side and the area of the triangle.

Sol: Perimeter of an isosceles triangle ABC in which AB = AC = 42 cm
Base = 2/3 times of the sum of equal sides
Let each equal side = a
Then base = 2/3 (2a) = (4/3)a
Perimeter = 42
∴ 2a + (4/3) a = 42
(10/3) a = 42 ⇒ a = (42×3)/10 = 126/10 = 12.6 cm
∴ Each equal side = 12.6 cm
and base = (4/3) × 12.6 = 4 × 4.2 = 16.8 cm

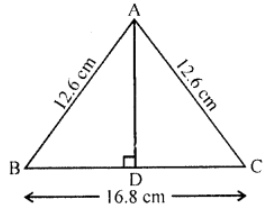
Let AD + BC is drawn which bisects BC at D
∴ BD = DC = 16.8/2 = 8.4
Now in right △ABD
AB2 = AD2 + BD2 (Pythagoras Theorem)
⇒ AD2 = AB2 – BD2
= (12.6)2 – (8.4)2
=158.76 – 70.56 = 88.20
∴ AD = √88.2 = 9.39
Area = (1/2) base × altitude
= (1/2) BC × AD = (1/2) × 16.8 × 9.39 cm²
= 8.4 × 9.39 = 78.888 cm²
= 78.89 cm²

Que-19: PQR is an isosceles triangle whose equal sides PQ and PR are 13 cm each, and the base QR measures 10 cm. PS is the perpendicular from P to QR and O is a point on PS such that ∠QOR = 90°. Find the area of shaded region.

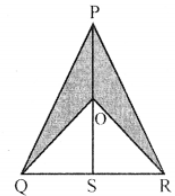
Sol: In isosceles △PQR, PQ = PR = 13 cm
Base QR = 10 cm
PS = QR which bisects QR at S
∴ QS = SR = 10/2 = 5 cm
Now in right △PQS,
PQ² = PS² + QS² (Pythagoras Theorem)
PS² = PQ² – QS²
= (13)² – (5)² = 169 – 25
= 144 = (12)²
∴ PS = 12 cm
Now area of △PQR = (1/2) base × altitude
= (1/2) × QS × PS
= (1/2) × 10 × 12 = 60 cm²
In isosceles △OQR
∠QOR = 90°
∴ ∠OQR = ∠ORS = 90°/2 = 45°
and ∠QOS = ∠ROS = 90°/2 = 45°
∴ OS = QS = 5 cm
Now area of △OQR = (1/2) × QR × OS
= (1/2) × 10 × 5 = 25 cm²
∴ Area of shaded portion = 60 – 25 = 35 cm²

Que-20: The perimeter of a right triangle is 50 cm and the hypotenuse is 18 cm. Find its area.

Sol: In △ABC, ∠B = 90°
AC = 18 cm and perimeter = 50 cm

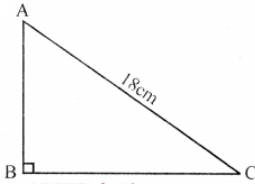
∴ AB + BC = 50 – 18 = 32 cm
Let AB = h
and BC = b
∴ Area = (1/2) AB × BC = (1/2) b.h …(i)
In right △ABC
AC² = AB² + BC²
⇒ (18)² = h² + b²
⇒ 324 = h² + b² …(ii)
∵ h + b = 32
Squaring we get,
(h+b)² = (32)² ⇒ h² + b² + 2hb = 1024
⇒ 324 + 2hb = 1024
⇒ 2hb = 1024 – 324 = 700
hb = 700/2 = 350
∴ Area = (1/2) hb = (1/2) × 350 = 175 cm²

— :  Area of Plane Figures Class 9 OP Malhotra Exe-16B ICSE Maths step by step Solutions  :–

Return to :–  OP Malhotra S Chand Solutions for ICSE Class-9 Maths

Thanks

Please Share with Your Friends