Area of Plane Figures Class 9 OP Malhotra Exe-16C ICSE Maths Solutions

Area of Plane Figures Class 9 OP Malhotra Exe-16C ICSE Maths Solutions Ch-16.  We Provide Step by Step Solutions / Answer of Area of parallelogram and rhombus for OP Malhotra Maths. Visit official Website CISCE  for detail information about ICSE Board Class-9 Mathematics.

Area of Plane Figures Class 9 OP Malhotra Exe-16C ICSE Maths Solutions Ch-16

Board	ICSE
Publications	S Chand
Subject	Maths
Class	9th
Chapter-16	Area of Plane Figures
Writer	OP Malhotra
Exe-16C	Solved Questions on Area of parallelogram and rhombus
Edition	2025-2026

Solved Questions on Area of Parallelogram and Rhombus

Area of Plane Figures Class 9 OP Malhotra Exe-16C ICSE Maths Solutions Ch-16

Que-1: Find the area of a parallelogram whose base and height are as given below.

Sol: (i) Base (b) = 8 cm
Height (h) = 3 cm
∴ Area = bh = 8 × 3 = 24 cm²

(ii) Base (b) = 2.8 cm
Height (h) = 5 cm
∴ Area = bh = 2.8 × 5 = 14 cm²

(iii) Base (b) = 12 mm
Height (h) = 8.7 mm
Area = bh = 12 × 8.7 = 104.4 mm²

(iv) Base (b) = 6.5 m
Height (h) = 4.8 m
Area = bh = 6.5 × 4.8 = 31.20 m²

Que-2: The area of a parallelogram is {1*(1/2)} area. Its base is 20 m. Find its height (1 are = 100 m²).

Sol: Area of a parallelogram = 1*(1/2) ares
= 1.5 × 100 = 150 m²
Base (b) = 20 m
Height (h) = Area / Base = 150/20 = 7.5 m

Que-3: In a parallelogram ABCD, AB = 8 cm, BC = 5 cm, perp. from A to DC = 3 cm. Find the length of the perp. drawn from B to AD.

Sol: In ||gm ABCD,
AB = 8 cm, BC = 5 cm
and perp. AL on DC = 3 cm
Let perp. BM on DA = x
Now area of the ||gm ABCD
= Base × Height
= DC × AL = 8 × 3 = 24 cm²
If base is AD = BC = 5 cm
Then height BM = Area / Base

Que-4: A parallelogram has sides 34 cm and 20 cm. One of its diagonals is 42 cm. Calculate its area.

Sol: In ||gm ABCD,
AB = 34 cm, AD = 20 cm
and diagonal BD = 42 cm
∵ Each diagonals of a ||gm bisect it into two triangles of equal area
∴ Area of ||gm ABCD = 2 area △ABD Now in △ABD,

Area of ||gm = 2 (area of ΔABD)
= 2 × 336 = 672 cm²

Que-5: ABCD is a parallelogram with side AB = 12 cm. Its diagonal AC and BD are of lengths 20 cm and 16 cm respectively. Find the area of ||gm ABCD.

Sol: Side AB of ||gm ABCD = 12 cm
Diagonal AC = 20 cm
and diagonal BD = 16 cm
∵ Diagonals of a ||gm bisect each other
∴ AO = OC = 20/2 = 10 cm
and BO = OD = 16/2 = 8 cm
Now area of △AOB with sides 12 cm, 10 cm, 8 cm

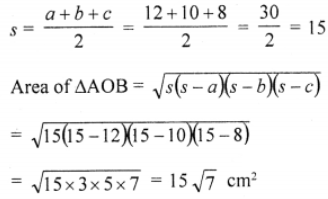
Diagonals of a ||gm form 4 equal triangles
∴ Area of ||gm ABCD = 4 × area △AOB
= 4 × 15 √7 = 60√7 cm²

Que-6: What is the area of a rhombus which has diagonals of 8 cm and 10 cm.

Sol: Diagonals of a rhombus ABCD are AC = 8 cm, BD= 10 cm
Area = Product of diagonals / 2 = (AC×BD)/2
= (8×10)/2 = 40 cm²

Que-7: The area of a rhombus is 98 cm². If one of its diagonals is 14 cm, what is the length of the other diagonal ?

Sol: Area of rhombus = 98 cm²
and length of one diagonal = 14 cm
Second diagonal = (Area ×2)/1st diagonal = (98×2)/14 = 14 cm²

Que-8: PQRS is a rhombus.
(i) If it is given that PQ = 3 cm, calculate the perimeter of PQRS.
(ii) If the height of the rhombus is 2.5 cm, calculate its area.
(iii) The diagonals of a rhombus are 8 cm and 6 cm respectively. Find its perimeter.

Sol: (i) In rhombus PQRS,
Side PQ = 3 cm
∴ Perimeter = 4 × side = 4 × 3 = 12 cm
(ii) Height of rhombus PQRS = 2.5 cm
∴ Area = base + height = 3 × 2.5 = 7.5 cm²

(iii) Diagonals are 8 cm and 6 cm of rhombus PQRS
∵ Diagonals of a rhombus bisect each other at right angles
∴ In right △POQ,
PO = 4 cm, QO = 3 cm
∴ PQ² = PO² + QO² (Pythagoras Theorem)
(4)² + (3)² = 16 + 9 = 25
= (5)²
∴ Side PQ = 5 cm
and perimeter = 4 × side = 4 × 5 = 20 cm

Que-9: The sides of a rhombus are 5 cm each and one diagonal is 8 cm, calculate,
(i) The length of the other diagonal and
(ii) The area of the rhombus.

Sol: Each side of rhombus = 5 cm
and one diagonal = 8 cm
∵ Diagonals of a rhombus bisect each other at right angle
(i) ∴ In right △AOB,
AO = (1/2) AC = 8/2 = 4 cm and BO = (1/2) BD
= AB² = AO² + BO²
(5)² = (4)² + BO²
⇒ 25 = 16 + BO²
⇒ BO² = 25 – 16 = 9 = (3)²
∴ BO = 3 cm
∴ BD = 2 × BO = 2 × 3 = 6 cm

(ii) Area = Product of diagonals / 2
= (8×6)/2 = 24 cm²

Que-10: In the figure, ABCX is a rhombus of side 5 cm. Angles BAD and ADC are right angles. If DC = 8 cm, calculate the area of ABCX.

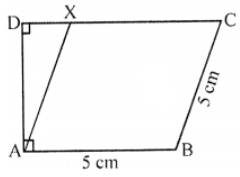
Sol: In the figure, ABCX is a rhombus with each side = 5 cm.
∠BAD and and ∠ADC are 90° each DC = 8 cm
∴ DX = DC – XC
= 8 – 5 = 3 cm
Now in right △ADX
AX² = AD² + DX² (Pythagoras Theorem)
(5)² = AD² + (3)²
25 = AD² + 9
⇒ AD² = 25 – 9 = 16 = (4)²
∴ AD = 4 cm

Now area of rhombus ABCX = base × height
= AB × AD
= 5 × 4 = 20 cm²

–; End of Area of Plane Figures Class 9 OP Malhotra Exe-16C ICSE Maths Solutions Ch-16 :–

Return to :–  OP Malhotra S Chand Solutions for ICSE Class-9 Maths

Thanks

Please Share with Your Friends