Area Theorem Class-9th Concise ICSE Maths Selina Solutions Chapter-16. We provide step by step Solutions of Exercise / lesson-16 Area Theorem for ICSE Class-9th Concise Selina Mathematics by R K Bansal.
Our Solutions contain all type Questions with Exe-16 B, Exe-16 B, Exe-16 C, to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-9th Mathematics .
Area Theorem Class-9th Concise ICSE Maths Selina Solutions Chapter-16
–: Select Topic :–
Exercise – 16 A, Area Theorem Class-9th Concise ICSE Maths Selina Solutions
Question 1
In the given figure, if area of triangle ADE is 60 cm2, state, given reason, the area of :
(i) Parallelogram ABED;
(ii) Rectangle ABCF;
(iii) Triangle ABE.
………………..
Answer
(i)ΔADE and parallelogram ABED are on the same base AB and between the same parallels DE//AB, so area of the triangle ΔADE is half the area of parallelogram ABED.
Area of ABED = 2 (Area of ADE) = 120 cm2
(ii)Area of parallelogram is equal to the area of rectangle on the same base and of the same altitude i.e, between the same parallels
Area of ABCF = Area of ABED = 120 cm2
(iii)We know that area of triangles on the same base and between same parallel lines are equal
Area of ABE=Area of ADE =60 cm2
Question 2
The given figure shows a rectangle ABDC and a parallelogram ABEF; drawn on opposite sides of AB. Prove that:
(i) Quadrilateral CDEF is a parallelogram;
(ii) Area of quad. CDEF
= Area of rect. ABDC
+ Area of // gm. ABEF.
……………..
Answer
After drawing the opposite sides of AB, we get
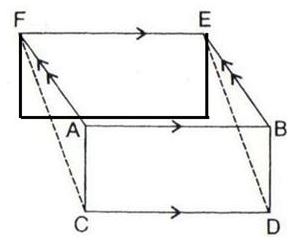
Since from the figure, we get CD//FE therefore FC must parallel to DE. Therefore it is proved that the quadrilateral CDEF is a parallelogram.
Area of parallelogram on same base and between same parallel lines is always equal and area of parallelogram is equal to the area of rectangle on the same base and of the same altitude i.e, between same parallel lines.
So Area of CDEF= Area of ABDC + Area of ABEF
Hence Proved
Question 3
In the given figure, diagonals PR and QS of the parallelogram PQRS intersect at point O and LM is parallel to PS. Show that:
…………………………
Answer
(i)
Since POS and parallelogram PMLS are on the same base PS and between the same parallels i.e. SP//LM.
As O is the center of LM and Ratio of area of triangles with same vertex and bases along the same line is equal to ratio of their respective bases.
The area of the parallelogram is twice the area of the triangle if they lie on the same base and in between the same parallels.
So 2(Area of PSO)=Area of PMLS
Hence Proved.
(ii)

Question 4
In parallelogram ABCD, P is a point on side AB and Q is a point on side BC.
Prove that:
………………
Answer

Given ABCD is a parallelogram. P and Q are any points on the sides AB and BC respectively, join diagonals AC and BD.
proof:
since triangles with same base and between same set of parallel lines have equal areas
area (CPD)=area(BCD)…… (1)
again, diagonals of the parallelogram bisects area in two equal parts
area (BCD)=(1/2) area of parallelogram ABCD…… (2)
from (1) and (2)
area(CPD)=1/2 area(ABCD)…… (3)
similarly area (AQD)=area(ABD)=1/2 area(ABCD)…… (4)
from (3) and (4)
area(CPD)=area(AQD),
hence proved.
(ii)
We know that area of triangles on the same base and between same parallel lines are equal
So Area of AQD= Area of ACD= Area of PDC = Area of BDC = Area of ABC=Area of APD + Area of BPC
Hence Proved
Question 5
In the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD.
If the area of parallelogram ABCD is 48 cm2;
(i) State the area of the triangle BEC.
(ii) Name the parallelogram which is equal in area to the triangle BEC.
Answer
(i)
Since triangle BEC and parallelogram ABCD are on the same base BC and between the same parallels i.e. BC//AD.
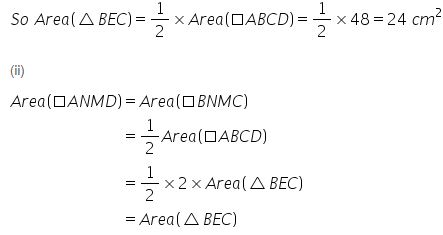
Therefore, Parallelograms ANMD and NBCM have areas equal to triangle BEC
Question 6
In the following figure, CE is drawn parallel to diagonals DB of the quadrilateral ABCD which meets AB produced at point E.
Prove that ΔADE and quadrilateral ABCD are equal in area.
Answer
Since ΔDCB and DEB are on the same base DB and between the same parallels i.e. DB//CE, therefore we get
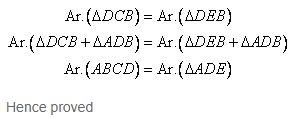
Question 7
ABCD is a parallelogram a line through A cuts DC at point P and BC produced at Q. Prove that triangle BCP is equal in area to triangle DPQ.
………….
Answer
ΔAPB and parallelogram ABCD are on the same base AB and between the same parallel lines AB and CD.

Question 8
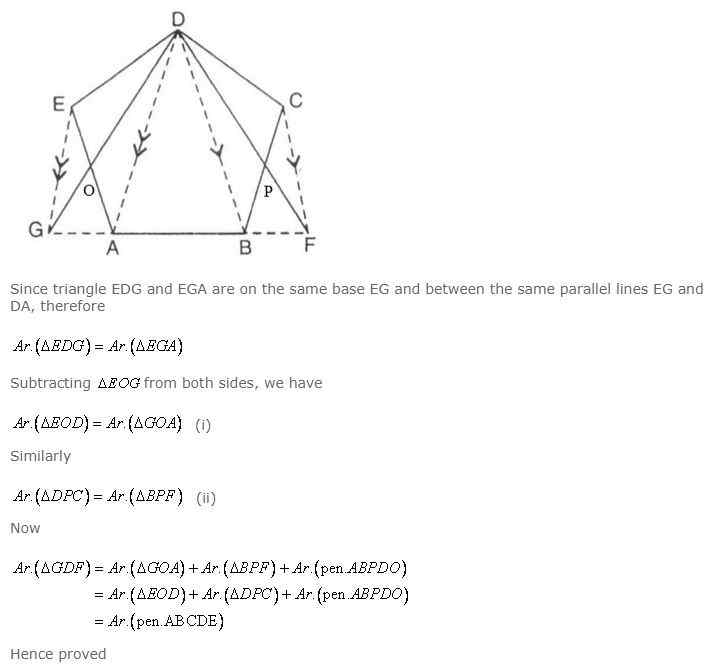
The given figure shows a pentagon ABCDE. EG drawn parallel to DA meets BA produced at G and CF draw parallel to DB meets AB produced at F.
Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.
…………………..
Answer
Question 9
In the given figure, AP is parallel to BC, BP is parallel to CQ. Prove that the area of triangles ABC and BQP are equal.
…………………..
Answer
Joining PC we get
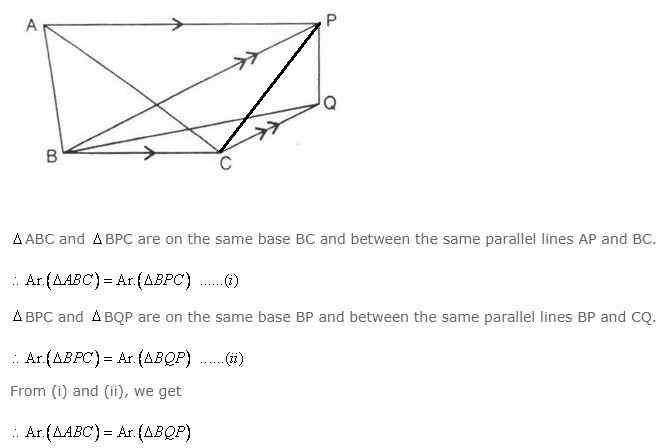
Hence proved.
Question 10
In the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.
…………..
(i) …………
(ii) Area of the square ABDE
= Area of the rectangle ARHF.
Answer
Question 11
In the following figure, DE is parallel to BC. Show that:
(i) Area (ΔADC) = Area(ΔAEB).
(ii) Area (ΔBOD) = Area (ΔCOE)..
………….
Answer

Hence Proved
(ii)
We know that area of triangles on the same base and between same parallel lines are equal
Area(triangle DBC)= Area(triangle BCE)
Area(triangle DOB) + Area(triangle BOC) = Area(triangle BOC) + Area(triangle COE)
So Area(triangle DOB) = Area(triangle COE)
Question 12
ABCD and BCFE are parallelograms. If area of triangle EBC = 480 cm2; AB = 30 cm and BC = 40 cm; Calculate;
(i) Area of parallelogram ABCD;
(ii) Area of the parallelogram BCFE;
(iii) Length of altitude from A on CD;
(iv) Area of triangle ECF.
………………..
Answer
Question 13
In the given figure, D is mid-point of side AB of ΔABC and BDEC is a parallelogram.
Prove that:
Area of ΔABC = Area of // gm BDEC.
Answer
Here AD=DB and EC=DB, therefore EC=AD

Adding quadrilateral CBDF in both sides, we have
Area of // gm BDEC= Area of ΔABC
Question 14
In the following, AC // PS // QR and PQ // DB // SR.
Prove that:
Area of quadrilateral PQRS = 2*Area of quad. ABCD.
Answer
In Parallelogram PQRS, AC // PS // QR and PQ // DB // SR.
Similarly, AQRC and APSC are also parallelograms.
Since ABC and parallelogram AQRC are on the same base AC and between the same parallels, then

Area of quadrilateral PQRS = 2 Area of quad. ABCD
Question 15
ABCD is trapezium with AB // DC. A line parallel to AC intersects AB at point M and BC at point N. Prove that: area of Δ ADM = area of Δ ACN.
Answer
Given: ABCD is a trapezium

AB || CD, MN || AC
Join C and M
We know that area of triangles on the same base and between same parallel lines are equal.
So Area of Δ AMD = Area of Δ AMC
Similarly, consider AMNC quadrilateral where MN || AC.
Δ ACM and Δ ACN are on the same base and between the same parallel lines. So areas are equal.
So, Area of Δ ACM = Area of Δ CAN
From the above two equations, we can say
Area of Δ ADM = Area of Δ CAN
Hence Proved.
Question 16
In the given figure, AD // BE // CF. Prove that area (ΔAEC) = area (ΔDBF)
…………..
Answer
We know that area of triangles on the same base and between same parallel lines are equal.
Consider ABED quadrilateral; AD||BE
With common base, BE and between AD and BE parallel lines, we have
Area of ΔABE = Area of ΔBDE
Similarly, in BEFC quadrilateral, BE||CF
With common base BC and between BE and CF parallel lines, we have
Area of ΔBEC = Area of ΔBEF
Adding both equations, we have
Area of ΔABE + Area of ΔBEC = Area of ΔBEF + Area of ΔBDE
=> Area of AEC = Area of DBF
Hence Proved
Question 17
In the given figure, ABCD is a parallelogram; BC is produced to point X. Prove that: area (Δ ABX) = area (quad. ACXD)
………………
Answer
Given: ABCD is a parallelogram.
We know that
Area of ΔABC = Area of ΔACD
Consider ΔABX,
Area of ΔABX = Area of ΔABC + Area of ΔACX
We also know that area of triangles on the same base and between same parallel lines are equal.
Area of ΔACX = Area of ΔCXD
From above equations, we can conclude that
Area of ΔABX = Area of ΔABC + Area of ΔACX = Area of ΔACD+ Area of ΔCXD = Area of ACXD Quadrilateral
Hence Proved
Question 18
The given figure shows parallelograms ABCD and APQR. Show that these parallelograms are equal in area.
[Join B and R]
Answer
Join B and R and P and R.
We know that the area of the parallelogram is equal to twice the area of the triangle, if the triangle and the parallelogram are on the same base and between the parallels
Consider ABCD parallelogram:
Since the parallelogram ABCD and the triangle ABR lie on AB and between the parallels AB and DC, we have

Area Theorem Class-9th Concise ICSE Maths Selina Solutions Exercise – 16 B,
Question 1
Show that:
(i) A diagonal divides a parallelogram into two triangles of equal area.
(ii) The ratio of the areas of two triangles of the same height is equal to the ratio of their bases.
(iii) The ratio of the areas of two triangles on the same base is equal to the ratio of their heights.
Answer
(i) Suppose ABCD is a parallelogram (given)
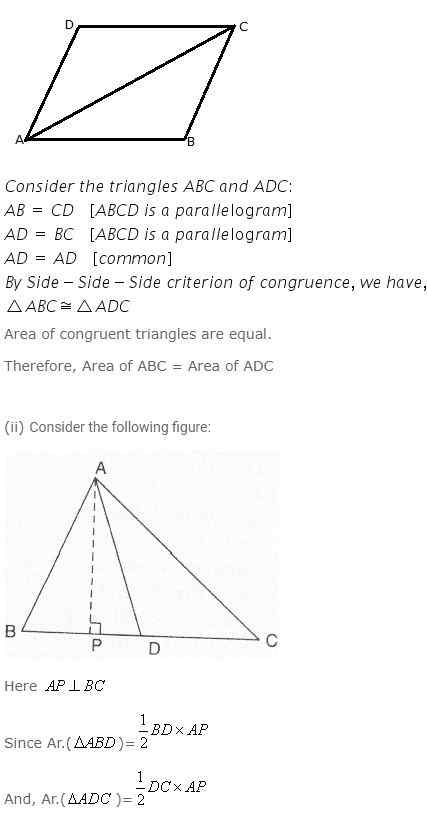
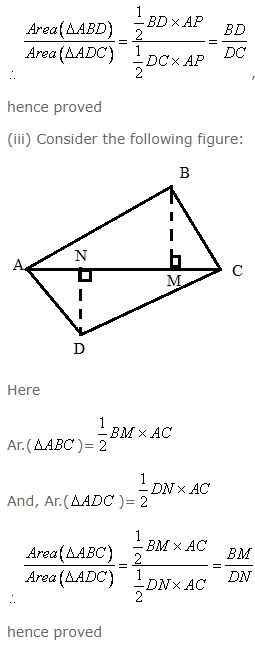
Question 2
In the given figure; AD is median of ΔABC and E is any point on median AD. Prove that Area (ΔABE) = Area (ΔACE).
Answer
AD is the median of ΔABC. Therefore it will divide ΔABC into two triangles of equal areas.
Area(ΔABD)= Area(ΔACD) (i)
ED is the median of EBC
Area(ΔEBD)= Area(ΔECD) (ii)
Subtracting equation (ii) from (i), we obtain
Area(ΔABD)- Area(ΔEBD)= Area(ΔACD)- Area(ΔECD)
Area (ΔABE) = Area (ΔACE). Hence proved
Question 3
In the figure of question 2, if E is the mid point of median AD, then prove that:
Area ……………….
Answer
Question 4
ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD respectively.
Prove that area of triangle APQ = 1/8 of the area of parallelogram ABCD.
Answer
We have to join PD and BD.

Question 5
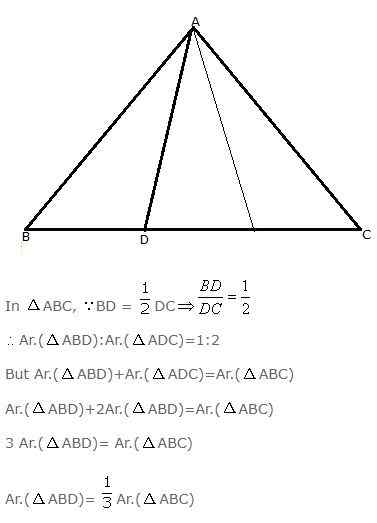
The base BC of triangle ABC is divided at D so that BD = 1/2 DC.
Prove that area of ΔABD = 1/3of the area of ΔABC.
Answer
Question 6
In a parallelogram ABCD, point P lies in DC such that DP: PC = 3:2. If area of ΔDPB = 30 sq. cm, find the area of the parallelogram ABCD.
Answer
Ratio of area of triangles with same vertex and bases along the same line is equal to ratio of their respective bases. So, we have
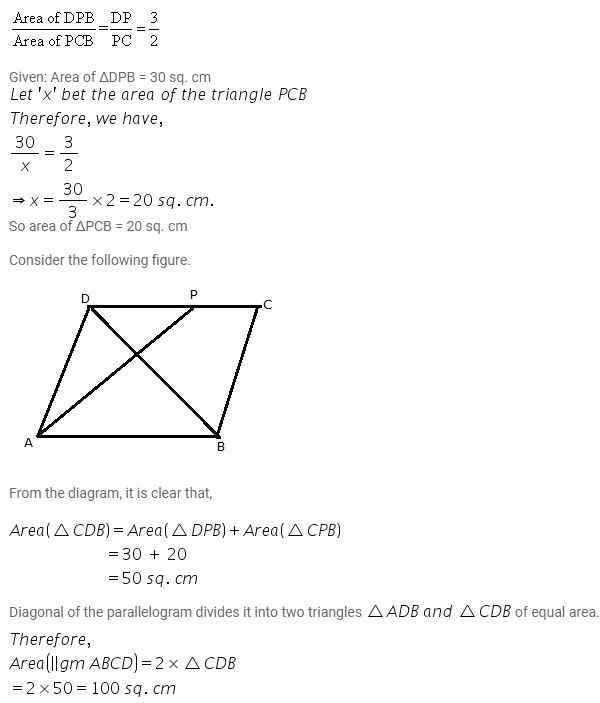
Question 7
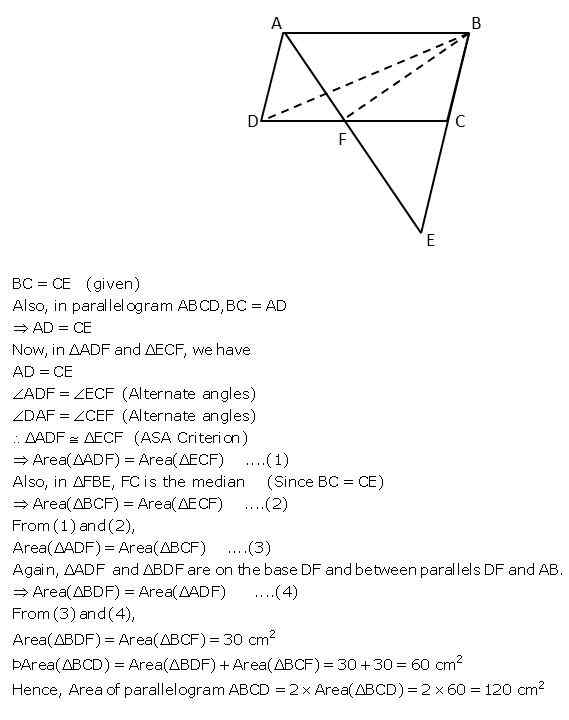
ABCD is a parallelogram in which BC is produced to E such that CE = BC and AE intersects CD at F.
If ar.(∆DFB) = 30 cm2; find the area of parallelogram
Answer
Question 8
The following figure shows a triangle ABC in which P, Q and R are mid-points of sides AB, BC and CA respectively. S is mid-point of PQ:
Prove that: ar.(∆ ABC) = 8 × ar.(∆ QSB)
………..
Answer
Class-9th Concise ICSE Maths Selina Solutions Exercise – 16 C Area Theorem
Question 1
In the given figure, the diagonals AC and BD intersect at point O. If OB = OD and AB//DC, show that:
(i) Area (Δ DOC) = Area (Δ AOB).
(ii) Area (Δ DCB) = Area (Δ ACB).
(iii) ABCD is a parallelogram.
……………
Answer
(i)
Ratio of area of triangles with same vertex and bases along the same line is equal to the ratio of their respective bases. So, we have:
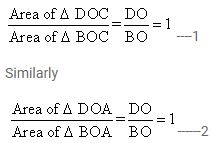
We know that area of triangles on the same base and between same parallel lines are equal.
Area of Δ ACD = Area of Δ BCD
Area of Δ AOD + Area of Δ DOC = Area of Δ DOC + Area of Δ BOC
=> Area of Δ AOD = Area of Δ BOC ——3
From 1, 2 and 3 we have
Area (Δ DOC) = Area (Δ AOB)
Hence Proved.
(ii)
Similarly, from 1, 2 and 3, we also have
Area of Δ DCB = Area of Δ DOC + Area of Δ BOC = Area of Δ AOB + Area of Δ BOC = Area of Δ ABC
So Area of Δ DCB = Area of Δ ABC
Hence Proved.
(iii)
We know that area of triangles on the same base and between same parallel lines are equal.
Given: triangles are equal in area on the common base, so it indicates AD|| BC.
So, ABCD is a parallelogram.
Hence Proved
Question 2 (Area Theorem Class-9th Concise)
The given figure shows a parallelogram ABCD with area 324 sq. cm. P is a point in AB such that AP:PB = 1:2 Find The area of Δ APD.
………
Answer
Ratio of area of triangles with the same vertex and bases along the same line is equal to the ratio of their respective bases.
So, we have

Question 3
In ΔABC, E and F are mid-points of sides AB and AC respectively. If BF and CE intersect each other at point O, prove that the ΔOBC and quadrilateral AEOF are equal in area.
Answer
E and F are the midpoints of the sides AB and AC.
Consider the following figure.

Question 4
In parallelogram ABCD, P is mid-point of AB. CP and BD intersect each other at point O. If area of ΔPOB = 40 cm2, and OP : OC = 1:2, find:
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD
Answer

Consider the triangles ΔPOB and ΔCOD
∠POB = ∠DOC …[ vertically opposite angles ]
∠OPB = ∠ODC …[ AB and DC are parallel, CP and BD are the transversals, alternate interior angles are equal ]
Therefore, by Angle-Angle similarly criterion of congruence, ΔPOB ∼ ΔCOD
Since P is the mid-point AP = BP, and AB = CD, we have CD = 2 BP
Therefore, We have,

⇒ Ar.( ΔDOC ) = 4Ar, ( ΔPOB )
= 4 x 40
= 160 cm2
Now consider Ar. ( ΔDBC ) = Ar. ( ΔDOC ) + Ar. (Δ BOC )
= 160 + 80
= 160 cm2
Two triangles are equal in the area if they are on equal bases and between the same parallels.
Therefore, Ar. ( ΔDBC ) = Ar. ( ΔABC ) = 240 cm2
The median divides the triangles into areas of two equal triangles.
Thus, CP is the median of the triangle ABC.
Hence, Ar. ( ΔABC ) = 2 Ar. ( ΔPBC )
Ar. ( ΔPBC ) =
Ar. ( ΔPBC ) = 120 cm2
( iii ) From part (ii) we have,
Ar. ( ΔABC ) = 2Ar. ( PBC ) = 240 cm2
The area of a triangle is half the area of the parallelogram if both are on equal bases and between the same parallels.
Thus, Ar. ( ΔABC ) = Ar. [ || gm ABCD ]
AR. [ || gm ABCD ] = 2 Ar. ( ΔABC )
AR. [ || gm ABCD ] = 2 x 240
AR. [ || gm ABCD ] = 480 cm2
Question 5
The medians of a triangle ABC intersect each other at point G. If one of its medians is AD, prove that:
(i) Area (ΔABD) = 3 Area (ΔBGD)
(ii) Area (ΔACD) = 3 Area (CGD)
(iii) Area (ΔBGC) = 1/3 Area (ΔABC)
Answer
The figure is shown below
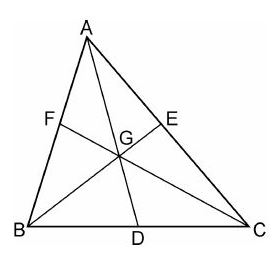
(i) Medians intersect at centroid.
Given that C is the point of intersection of medians and hence G is the centroid of the triangle ABC.
Centroid divides the medians in the ratio 2: 1
That is AG: GD = 2: 1.
Since BG divides AD in the ratio 2: 1, we have,
⇒ Area( ΔAGB ) = 2Area( ΔBGD )
From the figure, it is clear that,
Area( ΔABD ) = Area( ΔAGB ) + Area( ΔBGD )
⇒ Area( ΔABD ) = 2Area( ΔBGD ) + Area( ΔBGD )
⇒ Area( ΔABD ) = 3Area( ΔBGD ) ……(1)
(ii) Medians intersect at centroid.
Given that G is the point of intersection of medians and hence G is the centroid of the triangle ABC.
Centroid divides the medians in the ratio 2: 1
That is AG: GD = 2: 1.
Since CG divides AD in the ratio 2: 1, we have,
A( ΔAGC )/A( ΔCGD)=2/1
⇒ Area( ΔAGC ) = 2Area( ΔCGD )
From the figure, it is clear that,
Area( ΔACD ) = Area( ΔAGC ) + Area( ΔCGD )
⇒ Area( ΔACD ) = 2Area( ΔCGD ) + Area( ΔCGD )
⇒ Area( ΔACD ) = 3Area( ΔCGD ) ……(2)
(iii) Adding equations (1) and (2), We have,
Area( ΔABD ) + Area( ΔACD ) = 3Area( ΔBGD ) + 3Area( ΔCGD )
⇒ Area( ΔABC ) = 3[ Area( ΔBGD ) + Area( ΔCGD ) ]
⇒ Area( ΔABC ) = 3[ Area( ΔBGC ) ]
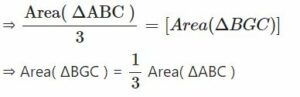
Question 6
The perimeter of a triangle ABC is 37 cm and the ratio between the lengths of its altitudes be 6 : 5 : 4. Find the lengths of its sides.
Let the sides be x cm, y cm and (37 – x – y) cm. Also, let the lengths of altitudes be 6a cm, 5a cm and 4a cm.
Answer
Consider that the sides be x cm, y cm, and (37 – x – y) cm. also, consider that the lengths of altitudes be 6a cm, 5a cm, and 4a cm
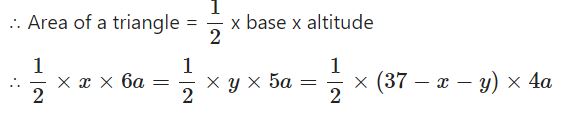
6x = 5y = 148 – 4x – 4y
6x = 5y and 6x = 148 – 4x – 4y
6x – 5y = 0 and 10x + 4y = 148
Solving both the equations, we have
X = 10 cm, y = 12 cm and ( 37 – x – y ) cm = 15cm.
Question 7 (Area Theorem Class-9th Concise)
In parallelogram ABCD, E is a point in AB and DE meets diagonal AC at point F. If DF: FE = 5:3 and area of ΔADF is 60 cm2; find
(i) area of ΔADE.
(ii) if AE: EB = 4:5, find the area of ΔADB.
(iii) also, find the area of parallelogram ABCD.
Answer
Question 8
In following figure ……………………..prove that
……………….
Answer

Question 9
In the following figure, OAB is a triangle and AB∥DC.
If the area of ∆ CAD = 140 cm2 and the area of ∆ ODC = 172 cm2, find
(i) the area of ∆ DBC
(ii) the area of ∆ OAC
(iii) the area of ∆ ODB.
Answer
Question 10
E, F, G and H are the mid- points of the sides of a parallelogram ABCD. Show that area of quadrilateral EFGH is half of the area of parallelogram ABCD.
Answer
Join HF.

Question 11
ABCD is a trapezium with AB parallel to DC. A line parallel to AC intersects AB at X and BC at Y. Prove that area of ∆ADX = area of ∆ACY.
Answer
Join CX, DX and AY.
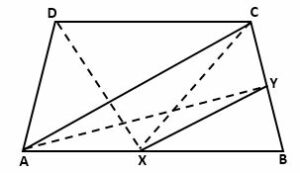
Now, triangles ADX and ACX are on the same base AX and between the parallels AB and DC.
∴ A(ΔADX) = A(ΔACX) ….(i)
Also, triangles ACX and ACY are on the same base AC and between the parallels AC and XY.
∴ A(ΔACX) = A(ΔACY) ….(ii)
From (i) and (ii), we get
A(ΔADX) = A(ΔACY)
— End of Area Theorem Class-9th Concise Selina Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -9