Arithmetic Mean, Median, Mode and Quartiles Class 10 OP Malhotra Exe-18D ICSE Maths Solutions Ch-18 Questions as latest prescribe guideline for upcoming exam. In this article you would learn How to Find Arithmetic Mode. Visit official Website CISCE for detail information about ICSE Board Class-10 Mathematics.

Arithmetic Mode Class 10 OP Malhotra Exe-18D ICSE Maths Solutions
| Board | ICSE |
| Publications | S Chand |
| Subject | Maths |
| Class | 10th |
| Chapter-18 | Arithmetic Mean, Median, Mode and Quartiles |
| Writer | OP Malhotra |
| Exe-18D | How to Find Arithmetic Mode |
| Edition | 2024-2025 |
Arithmetic Mode
The mode is one of the values of the measures of central tendency. This value gives us a rough idea about which of the items in a data set tend to occur most frequently
How to Find Arithmetic Mode
Count how many times each number appears in the data set
The number that appears the most is the mode
Exe-18D (Arithmetic Mode)
Arithmetic Mean, Median, Mode and Quartiles Class 10 OP Malhotra Exe-18D ICSE Maths Solutions Ch-18
Que-1: Find the mode of the following data :
(i) 8, 5, 6, 8, 8, 4, 6, 10, 8, 2;
(ii) 1, 2, 3, 3, 3, 5, 6, 8, 8, 8, 9;
(iii) 3, 5, 6, 6, 5, 3, 5, 3, 6, 5, 3, 5, 7, 6, 5, 7, 5;
(iv) 3, 4, 7, 11, 4, 3, 4, 5, 6, 4, 1, 4, 2, 4, 4.
Sol: (i) ∵ Frequency of 8 is 4 which is the greatest
∴ Mode = 4
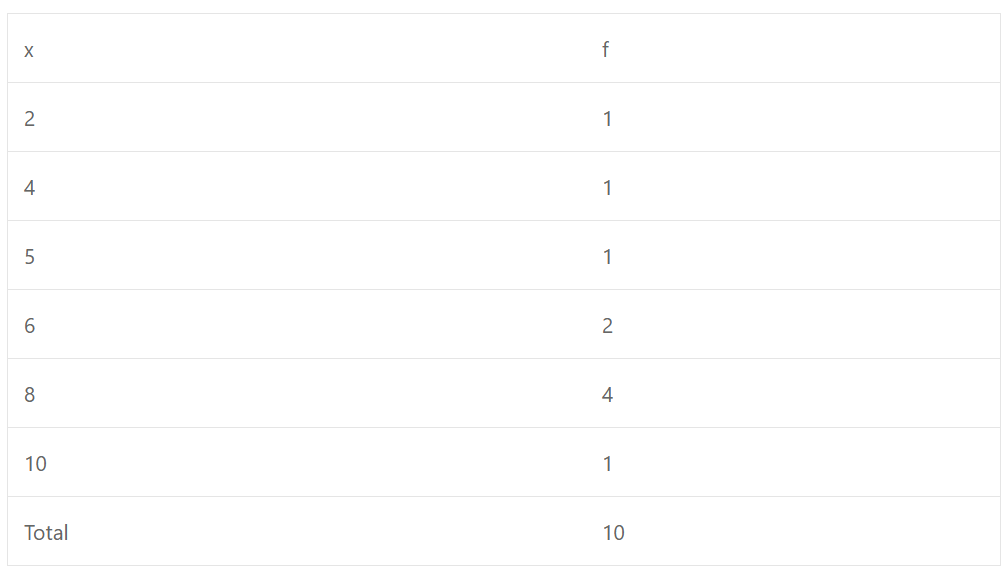
(ii) ∵ Frequency of 3 and 8 is 3 in each case
∴ Mode is 3 and 8 both
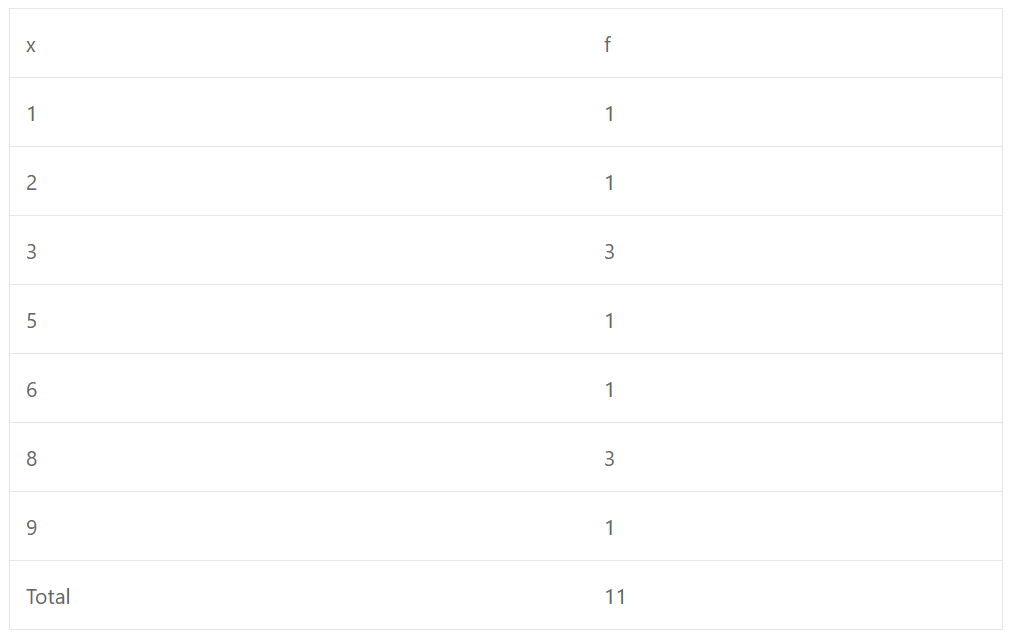
(iii) ∵ Frequency of 5 is the greatest
∴ Mode = 5
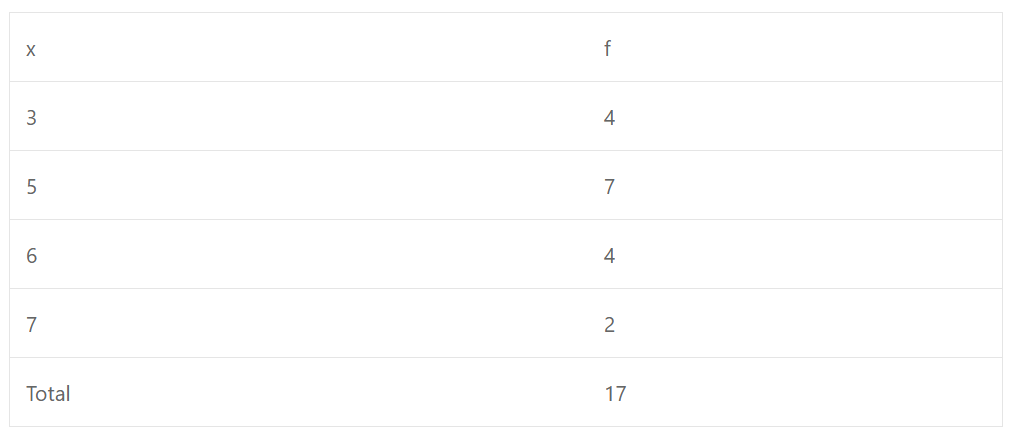
(iv) ∵ The frequency of 4 is the greatest
∴ Mode = 4
Que-2: Find the median and mode for the set of numbers : 2, 2, 3, 5, 5, 5, 6, 8, 9
Sol: Arranging in ascending order 2, 2, 3, 5, 5, 5, 6, 8, 9
Here n = 9 which is odd
∴ Median = (n+1)/2th term = (9+1)/2 = 5th term
Which is 5
∵ The frequency of 5 is the greatest
∴ Mode = 5
Que-3: A boy scored the following marks in various class tests during a term, each test being marked out of 20. 15, 17, 16, 7, 10, 12, 14, 16, 19, 12, 16
(i) What are his modal marks ?
(ii) What are his median marks ?
(iii) What are his mean marks ?
Sol: Arranging in ascending order,
7, 10, 12, 12, 14, 15, 16, 16, 16, 17, 19
(i) ∵ Frequency of 16 is the greatest
∴ Mode = 16
(ii) Here n= 11 which is odd
∴ Median = (n+1)/2th term = (11+1)/2 = 6th term
Which is 15
∴ Median = 15 marks
(iii) Mean = ∑xi/n
= (7+10+12+12+14+15+16+16+16+17+19)/11
= 154/11 = 14 Marks
Que-4: Find the mean, median and mode of the following marks obtained by 16 students in a class test marked out of 10 marks :
0, 0, 2, 2, 3, 3, 3, 4, 5, 5, 5, 5, 6, 6, 7, 8
Sol: (i) Mean = ∑xi/n
= (0+0+2+2+3+3+3+4+5+5+5+5+6+6+7+8)/16
= 64/16 = 4 marks
(ii) Median = 1/2[(n/2)+((n/2)+1)] th term
= 1/2[(16/2)+((16/2)+1)] th term
= 1/2[8+9]th term
= 1/2(4+5) = (1/2) 9 = 4.5 marks.
(iii) Mode
∵ 5 has greatest frequency
∴ Mode = 5 marks
Que-5: Find the mode from the following distributions :

Sol: Here in this distribution, frequency of 25 is greatest
∴ Mode = 25 marks
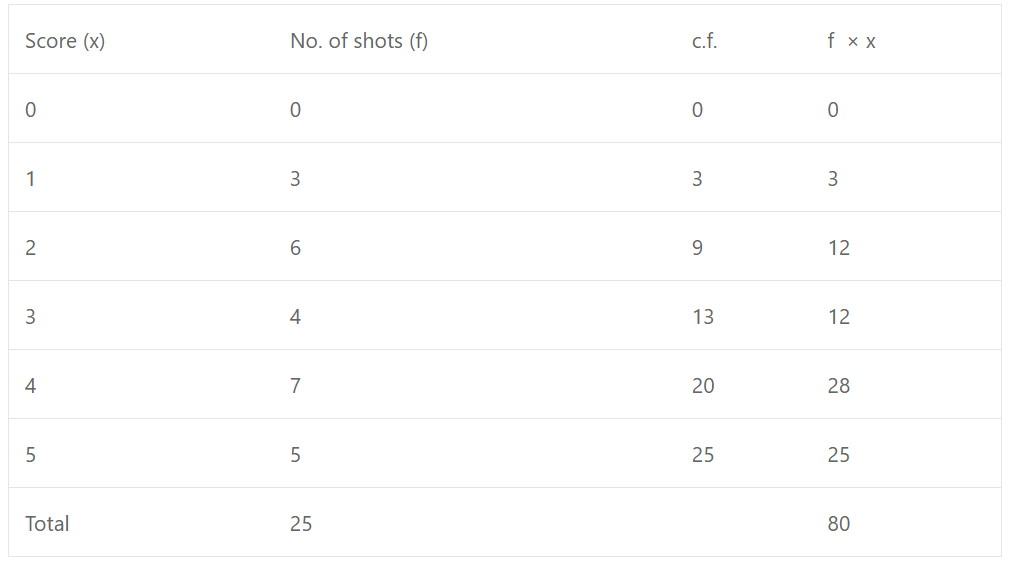
Que-6: At a shooting competition the scores of a competitor were as given below:

(i) What was his modal score ?
(ii) What was his median score ?
(iii) What was his total score ?
(iv) What was his mean score ?
Sol: (i) Modal score is 4
∵ It has the maximum frequency i.e. 7
∴ Mode = 4
(ii) Here n = 25
∴ Median = (n+1)/2 th term = (25+1)/2 th = 13 th term
Which is 3
∴ Median = 3
(iii) Total score = 80
(iv) Mean = ∑fx/∑f = 80/25 = 16/5 = 3.2
Que-7: For what value of x, the mode of the following data is 17 ?
15, 16, 17, 13, 17, 16, 14, , 17, 16, 15, 15
Sol: ∵ Mode = 17
∴ The data has 17 at the most
The given data except x can be vertex as
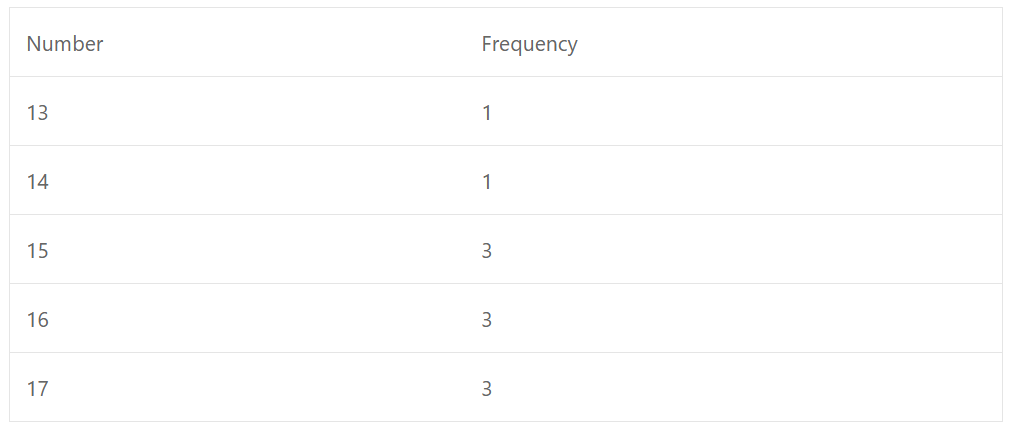
We see that frequency of 15, 26 and 17 is 3
∵ Mode = 17
∴ Frequency of 17 must be greater than of 15 or 16
∴ x = 17
Que-18: Find the value of k for which the mode of the following is 7 ?
3, 5, 5, 7, 3, 6, 7, 9, 6, 7, 3, 5, 7, 3, k
Sol: The given data except k, can be represented as given,
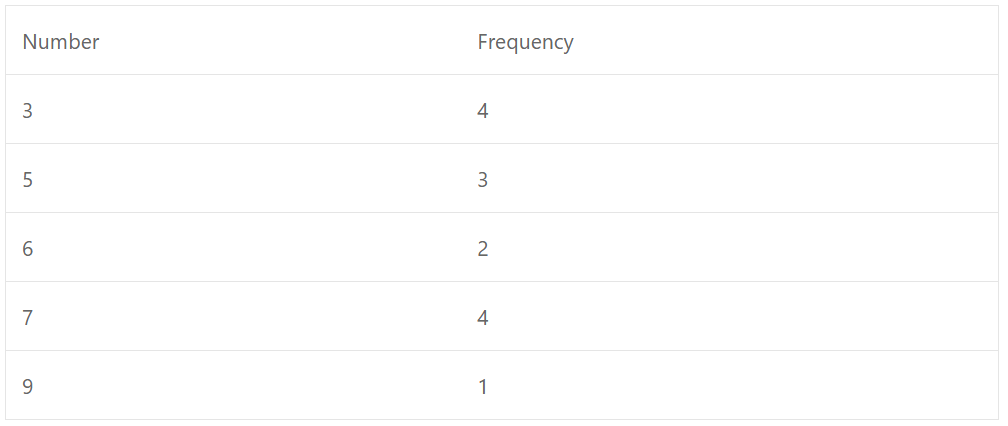
We see that frequency of 3 and 7 is 4 each
But mode = 7
∴ 7 has the greatest frequency or more than frequency of 3
∴ k = 7
Find the mode of the distributions given in problems 9-13 by drawing a histogram.
Que-9: A box contains nails of different lengths, measured to the nearest half centimeters the frequency distribution is as follows :
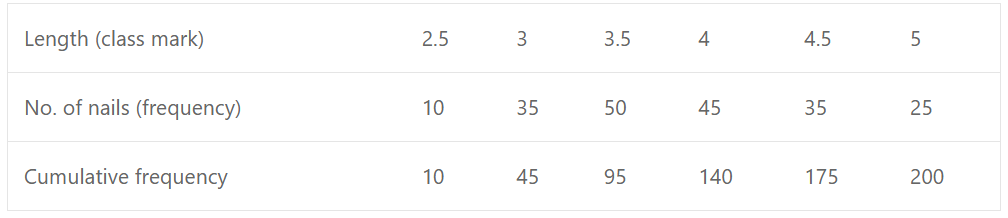
(i) State the upper boundary of the last class;
(ii) State the class size
(iii) State the modal class
(iv) Determine the class which contains the median of the distribution.
Sol: We are given class marks such as 2.5, 3, 3.5, 4 etc.
So, forming the classes accordingly :
2.25-2.75, 2.75-3.25, 3.25-3.75 etc.
Now

(i) Upper boundary of the last class is 5.25
(ii) Class size is 0.5
(iii) Modal class is 3.25-3.75 as it has the greatest frequency which is 50
(iv) Here n = 200
∴ Median = n/2th = 200/2 = 100th term
∴ Median lies between 96-140, which contains the class 3.75-4.25
–: End of Arithmetic Mean, Median, Mode and Quartiles Class 10 OP Malhotra Exe-18C ICSE Maths Solutions Ch-18 :–
Return to :- OP Malhotra S Chand Solutions for ICSE Class-10 Maths
Thanks
Please Share with Your Friend


