Banking Concise Maths Solution for ICSE Class 10 Chapter-2 .Concise Solution of Banking Chapter 2 for ICSE Maths Class 10 is also called Selina Publication . This post is Solution of Chapter – 2 Banking of Selina which is very famous Maths writer in ICSE Board in Maths Publication .Step by Step Solution of Chapter-2 Banking is given to understand the topic clearly . Chapter Wise Solution of concise including Chapter -2 Banking is very help full for ICSE Class 10th student appearing in 2020 exam of council.
Banking Concise Maths Solution for ICSE Class 10 Chapter-2
–: Select Exercise :-
Chapter-2 Banking Selina Concise Maths Solution for ICSE Class 10
Exercise- 2(A)
Question 1
Manish opens a Recurring Deposit Account with the Bank of Rajasthan and deposits 600 per month for 20 months. Calculate the maturity value of this account, if the bank pays interest at the rate of 10% per annum.
Answer 1
Instalment per month(P) = Rs600
Number of months(n) = 20
Rate of interest(r)= 10%p.a.
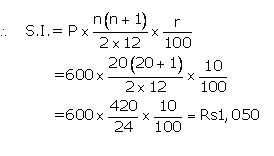
The amount that Manish will get at the time of maturity
=Rs(600×20)+ Rs1,050
=Rs12,000+ Rs1,050
= Rs13,050 Ans.
Question 2
Mrs. Mathew opened a Recurring Deposit Account in a certain bank and deposited 640 per month for 41/2 years. Find the maturity value of this account, if the bank pays interest at the rate of 12% per year.
Answer 2
Instalment per month(P) = Rs640
Number of months(n) = 54
Rate of interest(r)= 12%p.a.
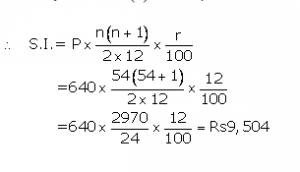
The amount that Manish will get at the time of maturity
=Rs(640×54)+ Rs9,504
=Rs34,560+ Rs9,504
= Rs44,064 Ans.
Question 3
Each of A and B both opened recurring deposit accounts in a bank. If A deposited![]() 1,200 per month for 3 years and B deposited
1,200 per month for 3 years and B deposited ![]() 1,500 per month for
1,500 per month for ![]() years; find, on maturity, who will get more amount and by how much? The rate of interest paid by the bank is 10% per annum.
years; find, on maturity, who will get more amount and by how much? The rate of interest paid by the bank is 10% per annum.
Answer 3
For A
Instalment per month(P) = Rs1,200
Number of months(n) = 36
Rate of interest(r)= 10%p.a.
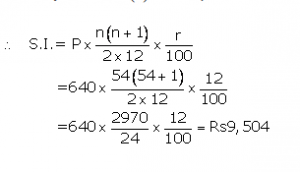
The amount that A will get at the time of maturity
=Rs(1,200×36)+ Rs6,660
=Rs43,200+ Rs6,660
= Rs49,860
For B
Instalment per month(P) = Rs1,500
Number of months(n) = 30
Rate of interest(r)= 10%p.a.
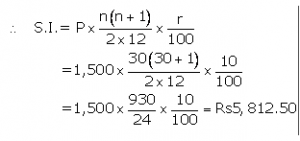
The amount that B will get at the time of maturity
=Rs(1,500×30)+ Rs5,812.50
=Rs45,000+ Rs5,812.50
= Rs50,812.50
Difference between both amounts= Rs50,812.50 – Rs49,860
= Rs952.50
Then B will get more money than A by Rs952.50 Ans.
Question 4
Ashish deposits a certain sum of money every month is a Recurring Deposit Account for a period of 12 months. If the bank pays interest at the rate of 11% p.a. and Ashish gets 12,715 as the maturity value of this account, what sum of money did money did he pay every month?
Answer 4
Let Instalment per month(P) = Rs y
Number of months(n) = 12
Rate of interest(r)= 11%p.a.
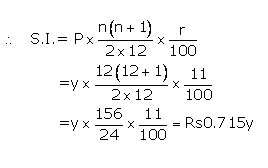
Maturity value= Rs(y x12)+Rs0.715y= Rs12.715y
Given maturity value= Rs12,715
Then Rs12.715y = Rs12,715
![]() Ans.
Ans.
Question 5
A man has a Recurring Deposit Account in a bank for 3½ years. If the rate of interest is 12% per annum and the man gets ![]() 10,206 on maturity, find the value of monthly installments.
10,206 on maturity, find the value of monthly installments.
Answer 5
Let Instalment per month(P) = Rs y
Number of months(n) = 42
Rate of interest(r)= 12%p.a.
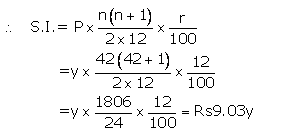
Maturity value= Rs(y x42)+Rs9.03y= Rs51.03y
Given maturity value= Rs10,206
Then Rs51.03y = Rs10,206
![]() Ans.
Ans.
Question 6
(i) Puneet has a Recurring Deposit Account in the Bank of Baroda and deposits 140 per month for 4 years. If he gets 8,092 on maturity, find the rate of interest given by the bank.
(ii) David opened a Recurring Deposit Account in a bank and deposited 300 per month for two years. If he received 7,725 at the time of maturity, find the rate of interest per annum.
Answer 6
(a)
Instalment per month(P) = Rs140
Number of months(n) = 48
Let rate of interest(r)= r %p.a.
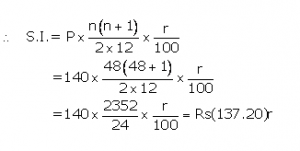
Maturity value= Rs(140 x48)+Rs(137.20)r
Given maturity value= Rs8,092
Then Rs(140 x48)+Rs(137.20)r = Rs8,092
137.20r = Rs8,092 -; Rs6,720
r =![]()
(b)
Instalment per month(P) = Rs300
Number of months(n) = 24
Let rate of interest(r)= r %p.a.
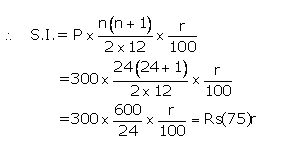
Maturity value= Rs(300 x24)+Rs(75)r
Given maturity value= Rs7,725
Then Rs(300 x24)+Rs(75)r = Rs7,725
75 r = Rs7,725 -; Rs7,200
r =![]()
Question 7
Amit deposited ![]() 150 per month in a bank for 8 months under the Recurring Deposit Scheme. What will be the maturity value of his deposits, if the rate of interest is 8% per annum and interest is calculated at the end of every month?
150 per month in a bank for 8 months under the Recurring Deposit Scheme. What will be the maturity value of his deposits, if the rate of interest is 8% per annum and interest is calculated at the end of every month?
Answer 7
Instalment per month(P) = Rs150
Number of months(n) = 8
Rate of interest(r)= 8%p.a.
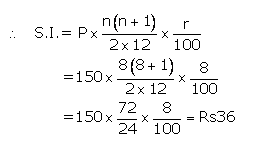
The amount that Manish will get at the time of maturity
=Rs(150×8)+ Rs36
=Rs1,200+ Rs36
= Rs1,236 Ans.
Question 8
Mrs. Geeta deposited ![]() 350 per month in a bank for 1 year and 3 months under the Recurring Deposit Scheme. If the maturity value of her deposits is
350 per month in a bank for 1 year and 3 months under the Recurring Deposit Scheme. If the maturity value of her deposits is ![]() 5,565; find the rate of interest per annum.
5,565; find the rate of interest per annum.
Answer 8
Instalment per month(P) = Rs350
Number of months(n) = 15
Let rate of interest(r)= r %p.a.
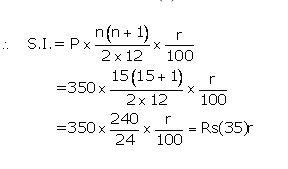
Maturity value= Rs(350 x15)+Rs(35)r
Given maturity value= Rs5,565
Then Rs(350 x15)+Rs(35)r = Rs5,565
35r = Rs5,565 -; Rs5,250
r =![]()
Question 9
A recurring deposit account of ![]() 1,200 per month has a maturity value of
1,200 per month has a maturity value of ![]() 12,440. If the rate of interest is 8% and the interest is calculated at the end of every month; find the time (in months) of this Recurring Deposit Account.
12,440. If the rate of interest is 8% and the interest is calculated at the end of every month; find the time (in months) of this Recurring Deposit Account.
Answer 9
Instalment per month(P) = Rs1,200
Number of months(n) = n
Let rate of interest(r)= 8 %p.a.

Maturity value= Rs(1,200x n)+Rs4n(n+1)= Rs(1200n+4n2+4n)
Given maturity value= Rs12,440
Then 1200n+4n2+4n = 12,440
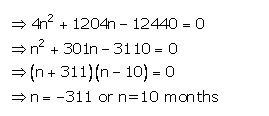
Then number of months = 10 Ans.
Question 10
Mr. Gulati has a Recurring Deposit Account of ![]() 300 per month. If the rate of interest is 12% and the maturity value of this account is
300 per month. If the rate of interest is 12% and the maturity value of this account is ![]() 8,100; find the time (in years) of this Recurring Deposit Account.
8,100; find the time (in years) of this Recurring Deposit Account.
Answer 10
Instalment per month(P) = Rs300
Number of months(n) = n
Let rate of interest(r)= 12 %p.a.
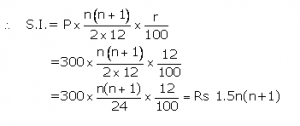
Maturity value= Rs(300x n)+Rs1.5n(n+1)
= Rs(300n+1.5n2+1.5n)
Given maturity value= Rs8,100
Then 300n+1.5n2+1.5n = 8,100
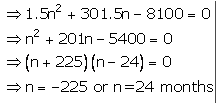
Then time= 2years
Question 11
Mr. Gupta opened a recurring deposit account in a bank. He deposited ![]() 2,500 per month for two years. At the time of maturity he got
2,500 per month for two years. At the time of maturity he got ![]() 67,500. Find:
67,500. Find:
(i) the total interest earned by Mr. Gupta
(ii) the rate of interest per annum.
Answer 11
(i)
Maturity value = Rs67,500
Money deposited= Rs2,500 x 24= Rs60,000
Then total interest earned= Rs67,500 – Rs60,000= Rs7,500 Ans.
(ii)
Instalment per month(P) = Rs2,500
Number of months(n) = 24
Let rate of interest(r)= r %p.a.
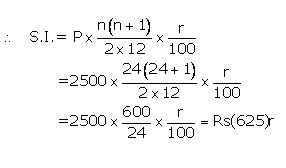
Then 625 r= 7500
![]()
Selina Maths Solution for ICSE Class 10th Chapter 2 – Banking
Exercise Ex. 2(B)
Question 1
Pramod deposits ![]() 600 per month in a Recurring Deposit Account for 4 years. If the rate of interest is 8% per year; calculate the maturity value of his account.
600 per month in a Recurring Deposit Account for 4 years. If the rate of interest is 8% per year; calculate the maturity value of his account.
Answer 1
Instalment per month(P) = Rs600
Number of months(n) = 48
Rate of interest(r)= 8%p.a.
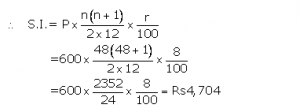
The amount that Manish will get at the time of maturity
=Rs(600×48)+ Rs4,704
=Rs28,800+ Rs4,704
= Rs33,504Ans.
Question 2
Ritu has a Recurring Deposit Account in a bank and deposits ![]() 80 per month for 18 months. Find the rate of interest paid by the bank if the maturity value of account is
80 per month for 18 months. Find the rate of interest paid by the bank if the maturity value of account is ![]() 1,554.
1,554.
Answer 2
Installment per month(P) = Rs80
Number of months(n) = 18
Let rate of interest(r)= r %p.a.
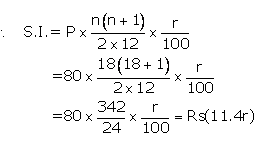
Maturity value= Rs(80 x18)+Rs(11.4r)
Given maturity value= Rs1,554
ThenRs(80 x18)+Rs(11.4r) = Rs1,554
![]() 11.4r = Rs1,554 – Rs1,440
11.4r = Rs1,554 – Rs1,440
![]()
Question 3
The maturity value of a R.D. Account is ![]() 16,176. If the monthly installment is
16,176. If the monthly installment is ![]() 400 and the rate of interest is 8%; find the time (period) of this R.D Account.
400 and the rate of interest is 8%; find the time (period) of this R.D Account.
Answer 3
Installment per month(P) = Rs400
Number of months(n) = n
Let rate of interest(r)= 8 %p.a.

Given maturity value= Rs16,176
ThenRs(400x n)+ ![]() = Rs16,176
= Rs16,176
1200n +4n2+4n= Rs48,528
4n2+1204n = Rs48,528
n2+301n – 12132= 0
(n+337)(n-36)=0
n= -337 or n=36
Then number of months = 36months= 3yearsAns.
Question 4
Mr. Bajaj needs ![]() 30,000 after 2 years. What least money (in multiple of
30,000 after 2 years. What least money (in multiple of ![]() 5) must he deposit every month in a recurring deposit account to get required money after 2 years, the rate of interest being 8% p.a.?
5) must he deposit every month in a recurring deposit account to get required money after 2 years, the rate of interest being 8% p.a.?
Answer 4
Let installment per month= Rs P
Number of months(n) = 24
Rate of interest®= 8%p.a.

Maturity value= Rs(P x 24)+ Rs 2P= Rs26P
Given maturity value= Rs30,000
_21Maynewformat_files/20140521155159_image037.gif)
Question 5
Mr. Richard has a recurring deposit account in a post office for 3 years at 7.5% p.a. simple interest. If he gets Rs. 8,325 as interest at the time of maturity, find:
- the monthly income
- the amount of maturity
Answer 5
Let the monthly deposit be P
Interest = Rs. 8,325
Rate of interest = 7.5%
Time = 3 years = 36 months

Question 6
Gopal has a cumulative deposit account and deposits 900 per month for a period of 4 years he gets 52,020 at the time of maturity, find the rate of interest.
Answer 6
Installment per month(P) = Rs900
Number of months(n) = 48
Let rate of interest(r)= r %p.a.
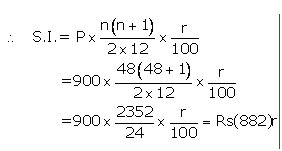
Maturity value= Rs(900 x48)+Rs(882)r
Given maturity value= Rs52,020
ThenRs(900 x48)+Rs(882)r = Rs52,020
882r = Rs52,020 – Rs43,200
r =![]()
Question 7
Deepa has a 4-year recurring deposit account in a bank and deposits ![]() 1,800 per month. If she gets
1,800 per month. If she gets ![]() 1,08,450 at the time of maturity, find the rate of interest.
1,08,450 at the time of maturity, find the rate of interest.
Answer 7
Installment per month(P) = Rs1,800
Number of months(n) = 48
Let rate of interest(r)= r %p.a.
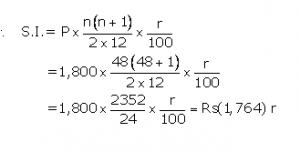
Maturity value= Rs(1,800 x48)+Rs(1,764)r
Given maturity value= Rs1,08,450
ThenRs(1,800 x48)+Rs(1764)r = Rs1,08,450
1764r = Rs1,08,450 – Rs86,400
r =![]()
Question 8
Mr. Britto deposits a certain sum of money each month in a Recurring Deposit Account of a bank. If the rate of interest is of 8% per annum and Mr. Britto gets Rs. 8,088 from the bank after 3 years, find the value of his monthly instalment.
Answer 8

Question 9

Question 10
Katrina opened a recurring deposit account with a Nationalised Bank for a period of 2 years. If the bank pays interest at the rate of 6% per annum and the monthly installment is Rs. 1,000, find the :
(i) interest earned in 2 years
(ii) maturity value
Answer 10

Question 11
Mohan has a recurring deposit account in a bank for 2 years at 6% p.a. simple interest. If he gets Rs. 1,200 as interest at the time of maturity, find:
(i) the monthly instalment
(ii) the amount of maturity.
Answer 11
Interest, I = Rs. 1,200
Time, n = 2 years = 2 × 12 = 24 months
Rate, r = 6%
(i) To find: Monthly instalment, P
Now,
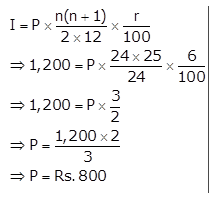
So, the monthly instalment is Rs. 800.
(ii) Total sum deposited = P × n = Rs. 800 × 24 = Rs. 19,200
∴ Amount of maturity = Total sum deposited + Interest on it
= Rs. (19,200 + 1,200)
= Rs. 20,400
– : End of Banking Concise Selina Solutions :-
Return to :- Concise Selina Maths Solutions for ICSE Class-10
Thanks
Please share with your friends


