ML Aggarwal Basic Geometrical Concept Exe-10.1 Class 6 ICSE Maths Solutions

ML Aggarwal Basic Geometrical Concept Exe-10.1 Class 6 ICSE Maths Solutions. We Provide Step by Step Answer of  Exe-10.1 Questions for Basic Geometrical Concept as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-6.

ML Aggarwal Basic Geometrical Concept Exe-10.1 Class 6 ICSE Maths Solutions

Board	ICSE
Publications	Avichal Publishig Company (APC)
Subject	Maths
Class	6th
Chapter-10	Basic Geometrical Concept
Writer	ML Aggarwal
Book Name	Understanding
Topics	Solution of Exe-10.1 Questions
Edition	2023-2024

Basic Geometrical Concept Exe-10.1

ML Aggarwal Class 6 ICSE Maths Solutions

Page-209

Question 1. How many lines can be drawn through a given point?

Answer :

Through a given point, an infinite number of lines can be drawn.

Question 2. How many lines can be drawn through two distinct given points?

Answer:

One

Question 3. How many lines can be drawn through three collinear points?

Answer :

one

Question 4. Mark three non-collinear points A, B and C in your note-book. Draw lines through these points taking two at a time and name these lines. How many such different lines can be drawn?

Answer:

lines AB, BC and CA; three.

Question 5. Use the figure to name :

(i) Five point
(ii) Aline
(iii) Four rays
(iv) Five line segments

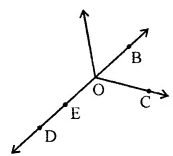
Answer:

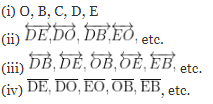
Question 6. Use the figure to name:

(i) Line containing point E.
(ii) Line passing through A.
(iii) Line on which point O lies.
(iv) Two pairs of intersecting lines.

Answer

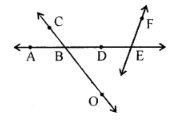
Question 7. From the given figure, write

(i) collinear points
(ii) concurrent lines and their points of concurrence.

Answer

(i) A, D, C ; B, D, E.
(ii) l, n, p ; point B and m, p, q ; point A.

---

Basic Geometrical Concept Exe-10.1

ML Aggarwal Class 6 ICSE Maths Solutions

Page-210

Question 8. In the given figure, write

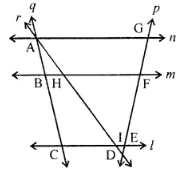
(i) all pairs of parallel lines.
(ii) all pairs of intersecting lines,
(iii) concurrent lines.
(iv) collinear points.

Answer:

(i) 1, m; 1, n; m, n
(ii) 1, p; m, p; n, p; 1, q; m, q;n, q; 1, r;m, r;n, r;p, q;p, r;q,r
(iii) n, r, quad
(iv) A, B, C; A, H, I, D; D, E, F, G; C, I, E; B, H, F

Question 11. Consider the following figure of line 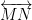. Says whether following statements are true or false in context of the given figure.

(i) Q, M, O, N and P are points on the line .
(ii) M, O and N are points on a line segment .
(iii) M and N are end points of line segment  .
(iv) O and N are end points of line segment .
(v) M is a point on the ray .
(vi) M is one of the end points of line segment .
(vii) Ray  is same as ray .
(viii)Ray  is not opposite to ray .
(ix) Ray  is different from ray .
(x) O is not an initial point of ray .
(xi) N is the initial point of  and .

Answer:

(i) True.
(ii) True.
(iii) True.
(iv) False.
(v) False.
(vi) False.
(vii) False.
(viii) False.
(ix) True.
(x) False.
(xi) True.

—  : End of ML Aggarwal Basic Geometrical Concept Exe-10.1 Class 6 ICSE Maths Solutions :–

Return to –  ML Aggarwal Maths Solutions for ICSE Class -6

Thanks