Centre of Mass Numerical Class-11 Nootan ISC Physics Solutions Ch-10. Step by step Solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-11 Physics.

Centre of Mass Numerical Class-11 Nootan ISC Physics Solutions
| Board | ISC |
| Class | 11 |
| Subject | Physics |
| Writer | Kumar and Mittal |
| Publication | Nageen Prakashan |
| Chapter-10 | Centre of Mass |
| Topics | Numerical on Position and Velocity of Centre of Mass |
| Academic Session | 2024-2025 |
Numerical on Position and Velocity of Centre of Mass
Class-11 Nootan ISC Physics Solutions Ch-10 Centre of Mass of Kumar and Mittal Physics of Nageen Prakashan
Question-1: Three point-masses of 1 g, 2 g and 3 g lie in the X-Y plane at respective points (1, 2), (0, -1) and (2,-3). Find the coordinates of the centre of mass of the system.
Answer- m1 = 1g , (1 , 2)
m2 = 2g , (0 , -1)
m3 = 3g , (2 , -3)
x = (m1 x1 + m2 x2 + m3 x3) / m1 + m2 + m3
=> (1 x 1 + 2 x 0 + 2 x 3) / 1 + 2 + 3 = 7/6.
y = (m1 y1 + m2 y2 + m3 y3) / m1 + m2 + m3
=> (1 x 2 + 2 x (-2) + 3 x (-3)) / 6 = -3/2.
Question-2: Three point-masses of 2 g, 3 g and 4 g are placed at the vertices of an equilateral triangle of side 1 metre. Find the centre of mass of the system.
Answer-

m1 = 2 (x1 , y1) = (0 , 0)
m2 = 3 (x2 , y2) = (1 , 0)
m3 = 4 (x3 , y3) = (1/2 , √3/2)
Now, co-ordinate of C.M
x = 2 x 0 + 3 x 1 + 4 x 1/2 / 2 + 3 + 4 = 5/9m
y = 2 x 0 + 3 x 0 + 4 x √3/2 / 9 = 2√3/9m
∴ co – ordinate of CM = (5/9m , 2√3/9m)
Question-3: Three identical spheres A, B and C, each of radius R, are placed touching one another on a horizontal table. Where is the centre of mass of the system located relative to A (say)?
Answer-
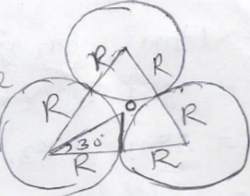
the position of three spheres can be taken as three same point masses at vertices of an equilateral triangle. where centre of mass will be its centroid.
that is => (R , R/√3)
Question-4: Particles of masses m₁ = 2 g, m₂ = 2 g, m3 = 1 g and m4 = 1 g are placed at the corners of a square of side L, as shown. Find the centre of mass of the system with respect to m₁.
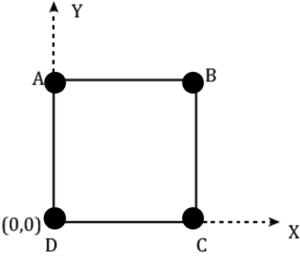
Answer-
m1 = 2 gm = (0 , 0)
m2 = 2 gm = (L , 0)
m3 = 1 gm = (L , L)
m4 = 1 gm = (0 , L)
now ,
x = 2 x 0 + 2 x L + 1 x L + 1 x 0 / 6 = L/2
y = 2 x 0 + 2 x 0 + 1 x L + 1 x L/6 = L/3
∴ co-ordinate of centre of mass = (L/2 , L/3).
Question-5: Two particles of masses 1.0 kg and 4.0 kg are 1 metre apart. Find the location of the centre of mass.
Answer- A = 1 kg , B = 4 kg
→xcm = m1 * x1 + m2 * x2 / m1 + m2
=> 1 * 0 + 4 x 1 / 5 = 0.8
=> 0.8 m from 1 kg mass.
Question-6: Two particles of masses 1 kg and 3 kg are moving with velocity (2i + 3 j) and (3i – 4j) m/s respectively. Calculate the velocity of centre of mass.
Answer- (→v = m1 →v1 + m2 →v2) / (m1 + m2)
=> 1 x (2i + 3j) + 3(3i – 4j)
=> 2i + 3j +9i -12j /4
=> 1/4 (11i + 9j).
Question-7: The distance between the centres of carbon and oxygen atoms in carbon monoxide gas molecule is 1.13 Å. Locate the centre of mass of the molecule relative to carbon atom.
Answer-
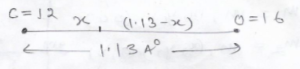
now according to definition of centre of mass
=> 12 * x = (1.13 – x) 16
=> 3x = 4(1.13 -x)
=> 3x = 4.52 – 4x
=> 7x = 4.52
=> x = 4.52/7 = 0.602 Å.
Question-8: Two point masses of 2 kg and 3 kg are moving along the same straight line with speeds 3 m/s and 5 m/s respectively. Find the speed of the centre of mass of the system, if both the masses are moving in:
(a) the same direction,
(b) in opposite direction
Answer- (a) for same direction
Vcm = m1 v1 + m2 v2 / m1 + m2
=> 2 x 3 – 5 x 3 / 5 = 4.2 m/s.
(b) for moving in opposite direction
=> 2 x 3 – 5 x 3/ 5 = -1.5 m/s.
Question-9: Two particles of masses 1 kg and 3 kg are located at (2i + 5j +13k) and (-6 i + 4 j – 2k) metre respectively. Find the position of their centre of mass.
Answer- →rcm = m1 →r1 + m2 →r2 / m1 + m2
=> 1(2i + 5j + 13k) + 3(-6i + 4j – 2k) / 4
=> -16i + 17j + 7k / 4
=> -4i + 17j/4 + 7k/4.
Question-10: Four particles of masses m, m, 2m and 2m are placed at the four corners of a square of side a. Find the centre of mass of the system.
Answer-

m1 = m = (0 , 0)
m2 = m = (a , 0)
m3 = 2m = (a , a)
m4 = 2m = (0 , a)
now,
x = m x 0 + m x a + 2m x a + 2m x 0 / 6m
=> a/2
y = m x 0 + m x 0 + 2m x a + 2m x a / 6m
=> 2a/3
∴ co-ordinates of C.M.
=> (a/2 , 2a/3).
—: end of Centre of Mass Numerical Numerical on Position and Velocity Class-11 Nootan ISC Physics Solutions Ch-10 :—
Return to : – Nootan Solutions for ISC Physics Class-11 Nageen Prakashan
Thanks
Please Share with your friends if helpful


