ML Aggarwal Circle Chapter Test Class 9 ICSE Maths Solutions Ch-15. Step by Step Solutions of Ch-Test Questions on Circle of ML Aggarwal for ICSE Class 9th Mathematics. Visit official website CISCE for detail information about ICSE Board Class-9.
ML Aggarwal Circle Chapter Test Class 9 ICSE Maths Solutions Ch-15
| Board | ICSE |
| Subject | Maths |
| Class | 9th |
| Chapter-15 | Circle |
| Topics | Solution of Ch-Test Questions |
| Academic Session | 2024-2025 |
Solution of Ch-Test Questions on Circle
ML Aggarwal Class 9 ICSE Maths Solutions Ch-15
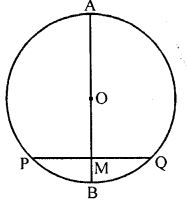
Question 1. In the given figure, a chord PQ of a circle with centre O and radius 15 cm is bisected at M by a diameter AB. If OM = 9 cm, find the lengths of :
(i) PQ, (ii) AP , (iii) BP
Answer : Radius = 15 cm
OA = OB = OP = OQ = 15 cm
Also, OM = 9 cm
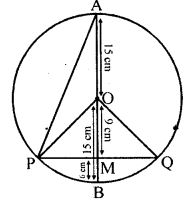
MB = OB – OM = 15 – 9 = 6 cm
AM = OA + OM =15 + 9 cm = 24 cm
In ∆OMP,
OP2 = OM 2 + PM2
⇒ 152 = 92 + PM2
⇒ PM2 = 255 – 81
⇒ PM = √144 = 12 cm
Also, In ∆OMQ
OQ2 = OM2 + QM2
⇒ 152 = OM2 + QM2
⇒ 152 = 92 + QM2 (QM2 = 225 – 81)
⇒ QM = √144 = 12 cm
⇒ PQ = PM + QM (As radius is bisected at M)
⇒ PQ = 12 + 12 cm = 24 cm
(ii) Now in ∆APM
AP2 = AM2 + OM2
⇒ AP2 =242 + 122
⇒ AP2 = 576 + 144
⇒ AP = √720 = 12 √5 cm
(iii) Now in ∆BMP
BP2 = BM2 + PM2
BP2 = 62 + 122
⇒ BP2 = 36 + 144
⇒ BP = √180 = 6√5 cm
Question 2. The radii of two concentric circles are 17 cm and 10 cm ; a line PQRS cuts the larger circle at P and S and the smaller circle at Q and R. If QR = 12 cm, calculate PQ.
Answer : A line PQRS intersects the outer circle at P
And S and inner circle at Q and R radius of
Outer circle OP = 17 cm and radius of inner
Circle OQ = 10 cm
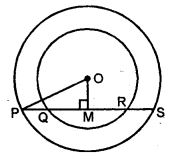
QR = 12 cm
From O, draw OM ⊥ PS
QM = ½ QR = ½ × 12 = 6 cm
In right ∆OQM
OQ2 = OM2 + QM2
⇒ (10)2 = OM2 + (6)2
⇒ OM2 = 102 – 62
⇒ OM2 = 100 – 36 = 64 = (8)2
⇒ OM = 8 cm
Now in right ∆OPM
OP2 OM2 + PM2
⇒ (17)2 = OM2 + PM2
⇒ PM2 = (17)2 – (8)2
⇒ PM2 = 289 – 64 = 225 = (15)2
⇒ PM = 15 cm
⇒ PQ = PM – QM = 15 – 6 = 9 cm
Question 3. A chord of length 48 cm is at a distance of 10 cm from the centre of a circle. If another chord of length 20 cm is drawn in the same circle, find its distance from the centre of the circle.
Answer : Perpendicular from Center on Chord bisect it
chord of length 48cm
48/2 = 24 cm
Distance from Center = 10 cm
Radius² = 24² + 10²
Radius² = 24² + 10²
Radius² = 26²
Radius = 26 cm
Let say chord of length is at Distance d from center
Then Chord length = 20 cm
20/2 = 10 cm
d² = 26² – 10²
d² = 24²
d = 24 cm
Question 4.
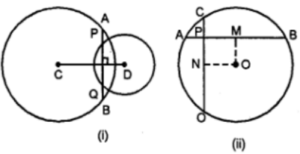
(a) In the figure (i) given below, two circles with centres C, D intersect in points P, Q. If length of common chord is 6 cm and CP = 5 cm, DP = 4 cm, calculate the distance CD correct to two decimal places.
(b) In the figure (ii) given below, P is a point of intersection of two circles with centres C and D. If the st. line APB is parallel to CD, Prove that AB = 2 CD.
Answer : (a)
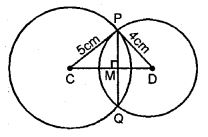

CD = CM + MD = 4 + 2.65
= 6.65
(b) Two circle with center C and D intersect each other at P and Q. A straight line APB is Drawn parallel to CD.
To prove : AB = 2 CD
Draw CM and DN perpendicular to AB from C and D
Proof CM ⊥ AP
AM = MP or AP = 2 MP
and DN ⊥ PB
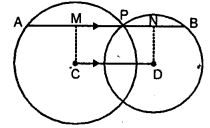
BN = PN or PB = 2 PN
Adding
AP + PB = 2 MP + 2 PN
AB = 2 (MP + PN) = 2 MN
AB = 2 CD
Question 5.
(a) In the figure (i) given below, C and D are centres of two intersecting circles. The line APQB is perpendicular to the line of centres CD. Prove that:
(i) AP=QB, (ii) AQ = BP.
(b) In the figure (ii) given below, two equal chords AB and CD of a circle with centre O intersect at right angles at P. If M and N are mid-points of the chords AB and CD respectively, Prove that NOMP is a square.
Answer :
(a) To circles with centers C and D intersect each other. A line APQB is drawn perpendicular to CD at M.
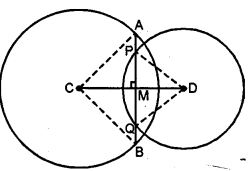
To prove : AP = QB
AQ = BP
Join AC and BC, DP and DQ
Proof : (i) In right triangle ACM and triangle BCM
AC = BC
CM = CM
ACM ≅ BCM
AM = BM
PD = QD
side DM = DM
PDM ≅ QDM
so, PM = QM
Subtracting
AM – PM = BM – QM
AP = QB
(ii) Adding PQ both sides,
AP + PQ = PQ + QB
AQ = PB
(b) Two chord AB and CD intersect each other at P right angle in the circle M and N are mid points of chord AB and CD
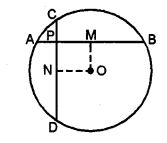
To prove : NOMP is a square
Proof : M and N are the mid-point of AB and CD respectively.
OM ⊥ AB and ON ⊥ CD
and OM = ON
AB ⊥ CD
OM ⊥ ON
Hence NOMP is a square
Question 6. In the given figure, AD is diameter of a circle. If the chord AB and AC are equidistant from its centre O, prove that AD bisects ∠BAC and ∠BDC.
Answer : AB and AC are equidistant from its centre O
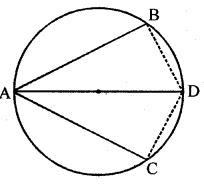
So, AB = AC
In triangle ABD and ACD
AB = AC
angle B = angle C
AD = AD
so, triangle ABD ≅ triangle ACD
AD bisects angle BAC and angle BCD
— : end of ML Aggarwal Circle Chapter Test Class 9 ICSE Maths Solutions Ch-15 : —
Return to :- ML Aggarawal Maths Solutions for ICSE Class-9
Thanks
Please Share with Your Friends


