ML Aggarwal Circles Chapter Test Class 10 ICSE Maths Solutions. We Provide Step by Step Answer of Chapter Test Questions for Circles as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Circles Chapter Test Class 10 ICSE Maths Solutions
| Board | ICSE |
| Subject | Maths |
| Class | 10th |
| Chapter-15 | Circles |
| Writer / Book | Understanding |
| Topics | Solutions of Chapter Test |
| Academic Session | 2024-2025 |
Chapter Test
ML Aggarwal Circles Class 10 ICSE Maths Solutions
(Page 373)
Question 1. In the figure given below ‘O’ is the centre of the circle. If QR = OP and ∠ORP = 20°. Find the value of ‘x ’ giving reasons.
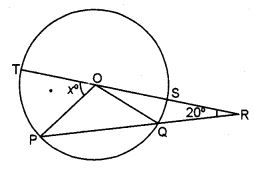
Answer :
Here, in ∆OPQ
OP = OQ = r
Also, OP = QR [Given]
OP = OQ = QR = r

In ∆OQR, OQ = QR
∠QOR = ∠ORP = 20°
And ∠OQP = ∠QOR + ∠ORQ
= 20° + 20°
= 40°
Again, in ∆ OPQ
∠POQ = 180° – ∠OPQ – ∠OQP
= 180°- 40° – 40°
= 100°
Now, x° + ∠POQ + ∠QOR = 180° [a straight angle]
x° + 100° + 20° = 180°
x° = 180° – 120° = 60°
Hence, the value of x is 60.
(ML Aggarwal Circles Chapter Test Class 10)
Question 2.
(a) In the figure (i) given below, triangle ABC is equilateral. Find ∠BDC and ∠BEC.
(b) In the figure (ii) given below, AB is a diameter of a circle with centre O. OD is perpendicular to AB and C is a point on the arc DB. Find ∠BAD and ∠ACD
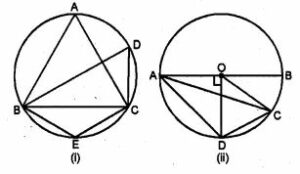
Answer :
(a) ∆ABC is an equilateral triangle.
Each angle = 60o
∠A = 60o
But ∠A = ∠D (Angles in the same segment)
∠D = 600
Now, ABEC is a cyclic quadrilateral,
∠A = ∠E = 180o
⇒ 60o + ∠E = 180o
⇒ 600 + ∠E = 180o (∠E = 180o – 60o)
⇒ ∠E = 120o
Hence, ∠BDC = 60o and ∠BEC = 120o
(b) AB is diameter of circle with centre O. OD ⊥ AB and C is a point on arc DB.
(i) In ∆AOD, ∠AOD = 90°
OA = OD (radii of the semi–circle)
∠OAD = ∠ODA
But ∠OAD + ∠ODA = 90o
⇒ ∠OAD + ∠ODA = 90o
⇒ 2∠OAD = 90o
⇒ ∠OAD = 90o/2 = 45°
Or ∠BAD = 45o
(ii) Arc AD subtends ∠AOD at the centre and ∠ACD at the remaining part of the circle.
∠AOD = 2 ∠ACD
⇒ 90o = 2 ∠ACD (OD ⊥ AB)
⇒ ∠ACD = 90o/2 = 45o
Question 3.
If ∠ADB = 55°, find x and y. Give reasons for your answers
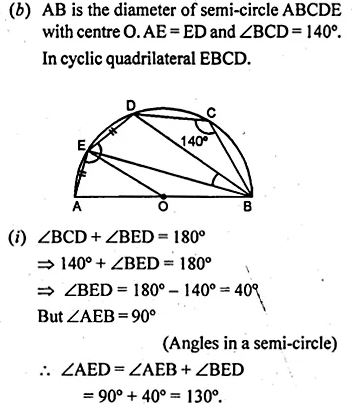
(b) In the figure given below, AB is the diameter of the semi-circle ABCDE with centre O. If AE = ED and ∠BCD = 140°, find ∠AED and ∠EBD. Also Prove that OE is parallel to BD.
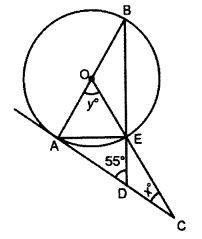

Answer :
(a) We know that angle between the radius and the tangent at the point of contact is right angle.


Circles Chapter Test
ML Aggarwal Class 10 ICSE Maths Solutions
(Page 374)
Question 4.
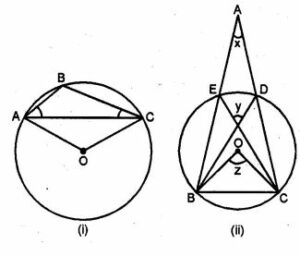
(a) In the figure (i) given below, O is the centre of the circle. Prove that ∠AOC = 2 (∠ACB + ∠BAC).
(b) In the figure (ii) given below, O is the centre of the circle. Prove that x + y = z.
Answer :
(a) Given: O is the centre of the circle.
To Prove : ∠AOC = 2 (∠ACB + ∠BAC).
Proof: In ∆ABC,
∠ACB + ∠BAC + ∠ABC = 180° (Angles of a triangle)
∠ABC = 180o – (∠ACB + ∠BAC) …(i)
In the circle, arc AC subtends ∠AOC at
The center and ∠ABC at the remaining part of the circle.
Reflex ∠AOC = 2 ∠ABC …(ii)
Reflex AOC = 2 {180o – (ACB + BAC)}
But ∠AOC = 360o – 2(∠ACB + ∠BAC)
But ∠AOC = 360o – reflex ∠AOC
= 360 ̊ – (360o – 2(∠ACB + ∠BAC)
= 360o – 360o + 2 (∠ACB + ∠BAC)
= 2 (∠ACB + ∠BAC)
Hence ∠AOC = 2 (∠ACB + ∠BAC)
(b) Given : in the figure, O is the center of the circle
To Prove : x + y = z.
Proof : Arc BC subtends ∠AOB at the center and ∠BEC at the remaining part of the circle.
∠BOC = 2 ∠BEC
But ∠BEC = ∠BDC (Angles in the same segment)
∠BOC = ∠BEC + ∠BDC …(i)
In ∆ABD
Ext. ∠y = ∠EBD +∠EBC
∠BEC = y – ∠EBD …(ii)
Similarly in ∆ABD
Ext. ∠BDC = x + ∠ABD
= x + ∠EBD …(iii)
Substituting the value of (ii) and (iii) in (i)
∠BOC = y – ∠EBD + x + ∠EBD = x + y
z = x + y
(ML Aggarwal Circles Chapter Test Class 10)
Question 5.
(a) In the figure (i) given below, AB is the diameter of a circle. If DC is parallel to AB and ∠CAB = 25°, find :
(i)∠ADC (ii) ∠DAC.

(b) In the figure give below sides AB and DC of a cyclic quadrilateral are produce to meet at a point P and the sides AD and BC are produce to meet at a point Q. If ∠ADC = 75° and ∠BPC = 50° , find ∠BAD and ∠CQD
Answer :
(a) AB is diameter and DC || AB,
∠CAB = 25°, join AD,BD

∠BAC = ∠BDC (Angles in the same segment)
But ∠ADB = 90° (Angles in a semi-circle)
∠ADC = ∠ADB + ∠BAC = 90° + 25° = 115°
∵ DC || AB (given)
∴ ∠CAB = ∠ACD (alternate angles)
∴ ∠ACD = 25°
Now in ΔACD,
∠DAC + ∠ADC + ∠ACD = 180° (Angles of a triangle)
⇒ ∠DAC + 115° + 25° = 180°
⇒ ∠DAC + 140° = 180°
⇒ ∠DAC = 180° – 140° = 40°
(b)
Angle BAD =55°
In triangle DAP,
50° +75°+ A = 180°
A = 180°-125°= 55°
Therefore, angle BAD = 55°
Question 6.
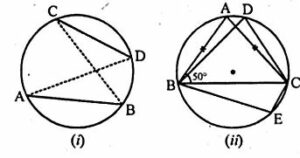
(a) In the figure (i) given below, ABCD is a cyclic quadrilateral. If AB = CD, Prove that AD = BC.
(b) In the figure (ii) given below, ABC is an isosceles triangle with AB = AC. If ∠ABC = 50°, find ∠BDC and ∠BEC.
Answer 6.
(a) Given : ABDC is a cyclic quadrilateral AB = CD.
To Prove: AD = BC.

Circles Chapter Test
ML Aggarwal Class 10 ICSE Maths Solutions
(Page 375)
Question 7. A point P is 13 cm from the centre of a circle. The length of the tangent drawn from P to the circle is 12 cm. Find the distance of P from the nearest point of the circle.
Answer :
Join OT, OP = 13 cm and TP = 12 cm
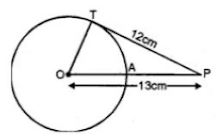
∵ OT is the radius
∴ OT ⊥ TP
Now in right ΔOTP
OP2 = OT2 + TP2
⇒ (13)2 = OT2 + (12)2
⇒ 169 = OT2 + 144
⇒ OT2 = 169 – 144
= 25
= (5)2
∴ OT = 5 cm
The nearest point A from P to cut circle over OA = radius of the circle = 5 cm.
∴ AP = OP – OA
= 13 – 5
= 8 cm
(ML Aggarwal Circles Chapter Test Class 10)
Question 8. Two circles touch each other internally. Prove that the tangents drawn to the two circles from any point on the common tangent are equal in length.
Answer :
Given: Two circles with centre O and O’ touch each other internally at P.
PT is any point on the common tangent of circles at P. From T, TA and TB are the tangents drawn to two circles.
To prove: TA = TB.
Proof : From T, TA and TP are the tangents to the first circle.
∴ TA = TP …(i)
Similarly, from T, TB and TP are the tangents to the second circle.
∴ TB = TP …(ii)
From (i) and (ii)
TA = TB
Question 9. From a point outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
(i) ∠AOP = ∠BOP.
(ii) OP is the perpendicular bisector of the chord AB.
Answer :
Given: From a point P, outside the circle with centre O.
PA and PB are the tangents to the circle,
OA, OB and OP are joined.
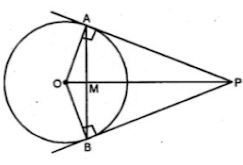
To prove: (i) ∠AOP = ∠BOP
(ii) OP is the perpendicular bisector of the chord AB.
Construction: Join AB which intersects OP at M.
Proof:
In right ΔOAP and OBP
Hypotenuse OP = OP (common)
Side OA = OB (radii of the same circle)
∴ ΔOAP ≅ ΔOBP (R.H.S axiom of congruency)
∴ ∠AOP = ∠BOP (C.P.C.T.)
And ∠APO = ∠BPO (C.P.C.T)
Now in ΔAPM and ΔBPM,
PM = PM (common)
∠APM = ∠BPM (proved)
AP = BP (tangents from P to the circle)
∴ ΔAPM ≅ ΔBPM (SAS axiom of congruency)
∴ AM = BM (C.P.C.T)
And ∠AMP = ∠BMP
But ∠AMP + ∠BMP = 180°
∴ ∠AMP = ∠BMP = 90°
∴ OP is perpendicular bisector of AB at M.
Question 10
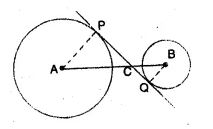
(a) The figure given below shows two circles with centers A, B and a transverse common tangent to these circles meet the straight line AB in C. Prove that:
AP : BQ = PC : CQ.
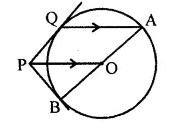
(b) In the figure (ii) given below, PQ is a tangent to the circle with centre O and AB is a diameter of the circle. If QA is parallel to PO, prove that PB is tangent to the circle.
Answer :
(a) Given: Two circles with centers A and B
and a transverse common tangent to these circles meets AB at C.

To prove : AP : BQ = PC : CQ
Proof : In ΔAPC and ΔBQC
∠PCA = ∠QCB (vertically opposite angles)
∠APC = ∠BQC (each 90°)
∴ ΔAPC ~ ΔBQC
∴ AP/BQ = PC/CQ
⇒ AP : BQ = PC : CQ
(b) Given : In the figure, O is the centre of the circle. AB is diameter. PQ is the tangent and QA || PO

To prove : PB is tangent to the circle
Construction: Join OQ
Proof : In ΔOAQ
OQ = OA (Radii of the same circle)
∴ ∠OQA = ∠POB (Corresponding angles)
And ∠OQA = ∠QOP (Alternate angles)
But ∠QAO = ∠OQA (Proved)
∠POB = ∠QOB
Now, in ΔOPQ and ΔOBP
OP = OP (Common)
OQ = OB (Radii of the same circle)
∠BOP = ∠POB (Proved)
∴ ΔOPQ ≅ ΔOBP (SAS axiom)
∴ ∠OQP = ∠OBP (c.p.c.t)
But ∠OQP = 90° (∵ PQ is tangent and OQ is the radius)
∴ ∠OBP = 90°
∴ PB is the tangent of the circle.
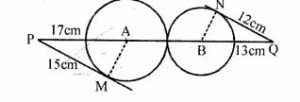
Question 11. In the figure given below, two circles with centers A and B touch externally. PM is a tangent to the circle with centre A and QN is a tangent to the circle with centre B. If PM = 15 cm, QN = 12 cm, PA = 17 cm and QB = 13 cm, then find the distance between the centers A and B of the circles.
Answer :
In the given figure, two chords with centre A and B touch externally.
PM is a tangent to the circle with centre A
and QN is tangent to the circle with centre B.
PM = 15 cm, QN = 12 cm, PA = 17 cm, QB = 13 cm.
We have to find AB.

AM is radius and PM is tangent
∴ AM ⊥ PM
Similarly, BN ⊥ NQ
Now in right ΔAPM,
AP2 = AM2 + PM2
⇒ 172 = AM2 + 152
⇒ AM2 = 172 – 152
= 289 – 225
= 64
= (8)2
∴ AM = 8 cm
Similarly in right ΔBNQ
BQ2 = BN2 + NQ2
⇒ 132 = BN2 + 122
⇒ 169 = BN2 + 144
BN2 = 169 – 144
= 25
= (5)2
∴ BN = 5 cm
Now AB = AM + BN (AR = AM and BR = BN)
= 8 + 5
= 13 cm
(ML Aggarwal Circles Chapter Test Class 10)
Question 12. Two chords AB, CD of a circle intersect externally at a point P. If PB = 7 cm, AB = 9 cm and PD = 6 cm, find CD.
Answer :
∵ AB and CD are two chords of a circle
which intersect each other at P, outside the circle.
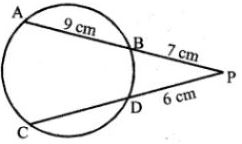
∴ PA × PB = PC × PD.
PB = 7 cm, AB = 9 cm, PD = 6 cm
AP = AB + BP
= 9 + 7
= 16 cm
∴ PA × PB = PC × PD
⇒ 16 × 7 = PC × 6
PC = (16 × 7)/6
= 56/3 cm
∴ CD = PC – PD
= 56/3 – 6
= 38/3
= 12.2/3 cm
Question 13.
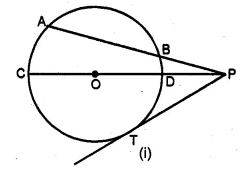
(a) In the figure (i) given below, chord AB and diameter CD of a circle with centre O meet at P. PT is tangent to the circle at T. If AP = 16 cm, AB = 12 cm and DP = 2 cm, find the length of PT and the radius of the circle
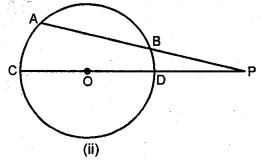
(b) In the figure (ii) given below, chord AB and diameter CD of a circle meet at P. If AB = 8 cm, BP = 6 cm and PD = 4 cm, find the radius of the circle. Also, find the length of the tangent drawn from P to the circle. .
Answer :
Given : (a) AB is a chord of a circle with centre O
and PT is tangent and CD is the diameter of the circle
which meet at P.
AP = 16 cm, AB = 12 cm, OP = 2 cm
∴PB = PA – AB = 16 – 12 = 4 cm
∵ABP is a secant and PT is tangent.
∴PT² = PA × PB.

= 16 × 4 = 64
= (8)2
⇒ PT = 8 cm
Again PT2 = PD × PC
⇒ (8)2 = 2 × PC
⇒ PC = (8 × 8)/2
⇒ PC = 32 cm
∴ CD = PC – PD
= 32 – 2
= 30 cm.
Radius of the circle = 30/2
= 15 cm
(b) Chord AB and diameter CD intersect each other at P outside the circle. AB = 8 cm, BP = 6 cm, PD = 4 cm.
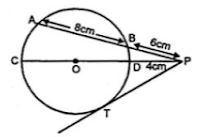
PT is the tangent to the circle drawn from P.
∵ Two chords AB and CD intersect each other at P outside the circle.
PA = AB +PB
= 8 + 6
= 14 cm
∴ PA × PB = PC × PD
⇒ 14 × 6 = PC × 4
⇒ PC = (14 × 6)/4
= 84/4
= 21 cm
∴ CD = PC – PD
= 21 – 4
= 17 cm
∴ Radius of the circle = 17/2
= 8.5 cm
(ii) Now PT is the tangent and ABP is secant.
∴ PT2 = PA × PB
= 14 × 6
= 84
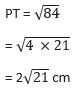
Circles Chapter Test
ML Aggarwal Class 10 ICSE Maths Solutions
(Page 376)
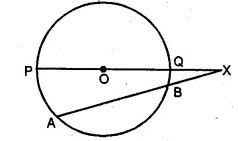
Question 14. In the adjoining figure given below, chord AB and diameter PQ of a circle with centre O meet at X. If BX = 5 cm, OX = 10 cm and. the radius of the circle is 6 cm, compute the length of AB. Also, find the length of tangent drawn from X to the circle.
Answer :
Chord AB and diameter PQ meet at X
on producing outside the circle
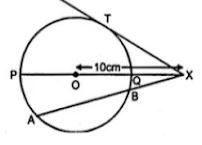
BX = 5 cm, OX = 10 cm and radius of the circle = 6 cm
∴ XP = XO + OP = 10 + 6 = 16 cm
XQ = XO – OQ
= 10 – 6
= 4 cm
∴ XB.XA = XP.XQ
⇒ 5.XA = 16 × 4
⇒ XA = (16 × 4)/5
= 64/5 cm
XA = 12.4/5 cm
∴ AB = XA – XB
= 12.4/5 – 5
= 7.4/5 cm
Now ∵ XT is the tangent of the circle.
∴ XT2 = XP. XQ
= 16 × 4
= 64
= (8)2
XT = 8 cm
(ML Aggarwal Circles Chapter Test Class 10)
Question 15.
(a) In the figure (i) given below, ∠CBP = 40°, ∠CPB = q° and ∠DAB = p°. Obtain an equation connecting p and q. If AC and BD meet at Q so that ∠AQD = 2 q° and the points C, P, B and Q are concyclic, find the values of p and q.
(b) In the figure (ii) given below, AC is a diameter of the circle with centre O. If CD || BE, ∠AOB = 130° and ∠ACE = 20°, find:
(i)∠BEC (ii) ∠ACB
(iii) ∠BCD (iv) ∠CED.
Answer :
(a)
(i) Given : ABCD is a cyclic quadrilateral.
Ext. ∠PBC = ∠ADC
⇒ 40° = ∠ADC
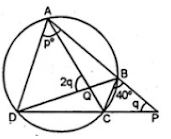
In ΔADP,
p + q + ∠ADP = 180°
p + q = 180° – ∠ADP
= 180° – ∠ADC
= 180° – 40°
= 140°
∴ p + q = 140°
(ii) ∵ C, P, B, Q are concyclic
∴ ∠CPB + ∠CQB = 180°
⇒ q + 2q = 180° (∵ ∠CQB = ∠DQA)
⇒ 3q = 180°
∴ q = 180°/3 = 60°
But p + q = 140°
∴ p + 60° = 140°
⇒ p = 140° – 60°
= 80°
Hence p = 80°, q = 60°
(b) ∠AOB = 130 ̊
But ∠AOB + ∠BOC = 180° (Linear pair)
⇒ 130° + ∠BOC = 180°
∠BOC = 180° – 130°
= 50°

(i) Now arc BC subtends ∠BOC at the centre and ∠BEC at the remaining part of the circle.
∠BEC = 1/2∠BOC
= ½ × 50°
= 25°
(ii) Similarly arc AB subtends ∠AOB at the centre and ∠ACE at the remaining part of the circle
∠ACB = 1/2∠AOB
= ½ × 130°
= 65°
(iii) ∵ CD || EB
∴ ∠ECD = ∠CEB (alternate angles)
= 25°
∴ ∠BCD = ∠ACB + ∠ACE + ∠ECD
= 65° + 20° + 25°
= 110°
(iv) ∵ EBCD is a cyclic quadrilateral
∴ ∠CED + ∠BCD = 180°
⇒ ∠CED + ∠BEC + ∠BCD = 180°
⇒ ∠CED + 25° + 110° = 180°
⇒ ∠CED + 135° = 180°
∴ ∠CED = 180° – 135°
= 45°
Question 16.
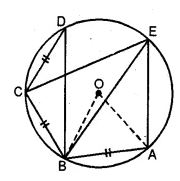
(a) In the figure (i) given below, chords AB, BC and CD of a circle with centre O are equal. If ∠BCD = 120°, find
(i) ∠BDC (ii) ∠BEC
(iii) ∠AEC (iv) ∠AOB.
Hence Prove that AOAB is equilateral.
Answer :
(a) In ∆BCD, BC = CD
∠CBD = ∠CDB
But ∠BCD + ∠CBD + ∠CDB = 180°
(∵ Angles of a triangle)
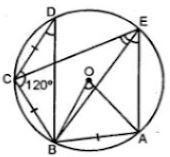
⇒ 120° + ∠CBD + ∠CBD = 180°
⇒ 120° + 2∠CBD = 180°
⇒ 2∠CBD = 180° – 120° = 60°
∴ ∠CBD = 30° and ∠CDB = 30°
∠BEC = ∠CDB (Angles in the same segment)
∴ ∠BEC = 30°
∵ CB = AB
∴ ∠BEC = ∠AEB (equal chords subtend equal angles)
∴ ∠AEB = 30°
Arc AB subtends ∠AOB at the centre and ∠AEB at the remaining part of the circle.
∴ ∠AOB = 2∠AEB
= 2 × 30°
= 60°
Now in ΔAOB
OA + OB (radii of the same circle)
∴ ∠OAB = ∠OBA
But ∠OAB + ∠OBA + ∠AOB = 180°
⇒ ∠OAB + ∠OAB + 60° = 180°
⇒ 2∠OAB = 180° – 60° = 120°
∴ ∠OAB = 60°
∠OAB = ∠OBA = ∠AOB = 60°
Hence OAB is an equilateral triangle.
(ML Aggarwal Circles Chapter Test Class 10)
Question 17.
(a) In the figure, (i) given below AB and XY are diameters of a circle with centre O. If ∠APX = 30°, find
(i) ∠AOX (ii) ∠APY (iii) ∠BPY (iv) ∠OAX.
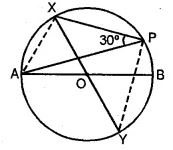
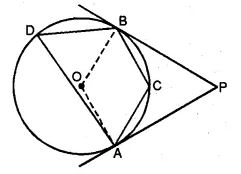
(b) In the figure (ii) given below, AP and BP are tangents to the circle with centre O. If ∠CBP = 25° and ∠CAP = 40°, find :
(i) ∠ADB (ii) ∠AOB (iii) ∠ACB (iv) ∠APB.
Answer :
(a) AB and XY are diameters of a circle with centre O.
∠APX = 30°.
To find :
(i) ∠AOX (ii) ∠APY
(iii) ∠BPY (iv) ∠OAX
(i) ∵ arc AX subtends ∠AOX at the centre and ∠APX at the remaining point of the circle.
∴ ∠AOX = 2 ∠APX
= 2 × 30°
= 60°
(ii) ∵ XY is the diameter
∴ ∠XPY = 90° (Angle in a semi-circle)
∴ ∠APY = ∠XPY – ∠APX
= 90° – 30°
= 60°
(iii) ∠APB = 90° (Angle in a semi-circle)
∠BPY = ∠APB – ∠APY
= 90° – 60°
= 30°
(iv) In ΔAOX,
OA = OX (radii of the same circle)
∴ ∠OAX = ∠OXA
But ∠AOX + ∠OAX + ∠OXA = 180° (Angles of a triangle)
⇒ 60° + ∠OAX + ∠OAX = 180°
⇒ 2∠OAX = 180°- 60°
= 120 ̊
∴ ∠OAX = 120°/2
= 60°
(b) Join CD

(i) ∠CDB = ∠CBP (Angles in the alternate segments)
∴ ∠CDB = 25° …(i)
Similarly, ∠CDA = ∠CAP = 40° (Angles in the alternate segments)
∴ ∠ADB = ∠CDA + ∠CDB
= 40° + 25°
= 65°
(ii) arc ACB subtends ∠AOB at the centre and ∠ADB at the remaining part of the circle.
∴ ∠AOB = 2∠ADB
= 2 × 65°
= 130°
(iii) ACBD is a cyclic quadrilateral
∴ ∠ACB + ∠ADB = 180°
⇒ ∠ACB + 65° = 180°
⇒ ∠ACB = 180° – 65°
= 115°
(iv) ∠AOB + ∠APB = 180°
⇒ 130° + ∠APB = 180°
⇒ ∠APB = 180° – 130°
= 50°
— : End of ML Aggarwal Circles Chapter Test Class 10 ICSE Maths Solutions : –
Return to: ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends


