ML Aggarwal Equation of Straight Line Ch-Test Class 10 ICSE Maths Solutions Ch-12

ML Aggarwal Equation of Straight Line Ch-Test Class 10 ICSE Maths Solutions Ch-12. We Provide Step by Step Answer of Ch-Test Questions for Equation of Straight Line as council prescribe guideline for upcoming board exam. Visit official Website CISCE  for detail information about ICSE Board Class-10.

ML Aggarwal Equation of Straight Line Ch-Test Class 10 ICSE Maths Solutions Ch-12

Board	ICSE
Subject	Maths
Class	10th
Chapter-12	Equation of Straight Line
Writer / Book	Understanding
Topics	Solutions of Ch-Test
Academic Session	2024-2025

 Ch-12 Equation of Straight Line Ch-Test

 ML Aggarwal Solutions of Class 10 for ICSE Maths

Question- 1

Find the equation of a line whose inclination is 60° and y-intercept is – 4.

Answer- 1

Angle of inclination = 60°
Slope = tan θ = tan 60° = √3
Equation of the line will be,
y = mx + c = √3x + ( – 4)
⇒ y – √3x – 4

Question -2

Write down the gradient and the intercept on the y-axis of the line 3y + 2x = 12.

Answer- 2

Slope of the line 3y + 2x = 12
⇒ 3y = 12 – 2x
⇒ 3y = -2x + 12

y = (-2/3) x + 12/3

y = (-2/3) x + 4

Hence, gradient = -2/3 and the intercept on the y-axis is 4.

Question -3

If the equation of a line is y – √3x + 1, find its inclination.

Answer -3

In the line
y = √3 x + 1
Slope = √3
⇒ tan θ = √3
⇒ θ = 60° (∵ tan 60° = √3)

Question -4

If the line y = mx + c passes through the points (2, – 4) and ( – 3, 1), determine the values of m and c.

Answer- 4

The equation of line y = mx + c
∵ it passes through (2, – 4) and ( – 3, 1)
Now substituting the value of these points -4 = 2m + c …(i)
and 1 = -3m + c …(ii)
Subtracting we get,

-5 = 5m

⇒ m = -5/5 = -1

Substituting the value of m in (i)

-4 = 2(-1) + c

⇒ -4 = -2 + c

c = -4 + 2 = -2

∴ m = -1, c = -2

Question -5  

If the point (1, 4), (3, – 2) and (p, – 5) lie on a  line, find the value of p.

Answer- 5

Let the points to be A (1, 4), B (3, -2) and C (p, -5) are collinear and let B (3, -2)
divides AC in the ratio of m₁ : m₂

∴ x = (m₁x₂ + m₂x₁)/(m₁ + m₂)

⇒ 3 = (m₁p + m₂×1)/(m₁ + m₂)

3m₁ + 3m₂ = m₁p + m₂

⇒ 3m₁ – m₁p = m₂ – 3m₂

⇒ m₁(3 – p) = -2 m₂

⇒ m₁/m₂ = – 2/(3 – p) …(i)

and –2 = {m₁(-5) + m₂×4}/(m₁ + m₂)

⇒ -2m₁ – 2m₂ = – 5m₁ + 4m₂

⇒ -2m₁ + 5m₁ = 4 m₂ + 2m₂

⇒ 3m₁ = 6 m₂

⇒ m₁/m₂ = 6/3 = 2 …(ii)

From (i) and (ii)

-2/(3–p) = 2

⇒ -2 = 6 – 2p

⇒ 2p = 6 + 2 = 8

⇒ p = 8/2 = 4

Question- 6

Find the inclination of the line joining the points P (4, 0) and Q (7, 3).

Answer -6

Slope of the line joining the points P (4, 0) and Q (7, 3)

= (y₂ – y₁)/(x₂ – x₁) = (3–0)/(7–4) = 3/3 = 1

∴ tan θ = 1

⇒ θ = 45° (∵ tan 45° = 1)

Hence inclination of line = 45°

Question -7

Find the equation of the line passing through the point of intersection of the lines 2x + y = 5 and x – 2y = 5 and having y-intercept equal to -3/7

Answer -7

Equation of lines are
2x + y = 5 …(i)
x – 2y = 5 …(ii)
Multiply (i) by 2 and (ii) by 1, we get
4x + 2y = 10
x – 2y = 5
Adding we get,

5x = 15

⇒ x = 15/5 = 3

Substituting the values of x in (i)

2×3 + y = 5

⇒ 6 + y = 5

⇒ y = 5 – 6

= -1

∴ Co-ordinates of point of intersection are (3, -1)

∵ the line passes through (3, -1)

∴ -1 = m×3 – 3/7 (y = mx + c)

3m = -1 + 3/7 = -4/7

m = -4/(7×3)

= -4/21

∴ Equation of line y = -4/21 ×x – 3/7

⇒ 21y = -4x – 9

⇒ 4x + 21y + 9 = 0

Question -8  

If the lines  x/3 + y/4 = 7 and 3x + ky = 11 are perpendicular to each other, find the value of k.

Answer -8

Given Equation of lines are

x/3 + y/4 = 7

⇒ 4x + 3y = 84

⇒ 3y = -4x + 84

⇒ y = -4/3 ×x + 28 …(i)

And 3x + ky = 11

⇒ ky = -3x + 11

⇒ y = (-3/k)×x + 11/k …(ii)

Let slope of line (i) be m₁ and of (ii) be m₂

∴ m₁ = -4/3 and m₂ = -(3/k)

∵ These lines are perpendicular to each other

∴ m₁m₂ = – 1

⇒ -4/3 × (-3/k) = -1

⇒ 4/k = -1

⇒ – k = 4

⇒ k = – 4

Question -9

Write down the equation of a line parallel to x – 2y + 8 = 0 and passing through the point (1, 2).

Answer -9

The equation of the line is x – 2y + 8 = 0
⇒ 2y = x + 8

⇒ y = (1/2)×x + 4

∴ Slope of the line = 1/2

∴ Slope of the line parallel to the given line passing through (1, 2) = 1/2

∴ Equation of the lines will be,

y – y₁ = m(x – x₁)

⇒ y – 2 = 1/2 (x – 1)

⇒ 2y – 4 = x – 1

⇒ x – 2y – 1 + 4 = 0

⇒ x – 2y + 3 = 0

Question-10

Write down the equation of the line passing through ( – 3, 2) and perpendicular to the line 3y = 5 – x.

Answer-10

Equations of the line is
3y = 5 – x ⇒ 3y = -x + 5

⇒ y = -(1/3)×x + 5/3

∴ Slope of the line = -1/3

And slope of the line perpendicular to it and passing through (-3, 2) will be = 3

(∵ m₁m₂ = -1)

∴ Equation of the line will be

y – y₁ = m(x – x₁)

⇒ y – 2 = 3(x + 3)

⇒ y – 2 = 3x + 9

⇒ 3x – y + 9 + 2 = 0

⇒ 3x – y + 11 = 0

Question-11  

Find the equation of the line perpendicular to the line joining the points A (1, 2) and B (6, 7) and passing through the point which divides the line segment AB in the ratio 3 : 2.

Answer-11

Let slope of the line joining the points A (1, 2) and B (6, 7) be m₁

∴ m₁ = (y₂ – y₁)/(x₂ – x₁)

= (7–2)/(6–1)

= 5/5

= 1

Let m₂ be the slope of the line perpendicular to it then m₁×m₂ = -1

⇒ 1×m₂ = -1

∴ m₂ = -1

Let the point P (x, y) divides the line AB in the ratio of 3 : 2

∴ x = (m₁x₂ + m₂x₁)/(m₁ + m₂)

= {3×6 + 2×1)/(3 + 2)

= (18+2)/5

= 20/5

= 4

And y = (m₁y₂ + m₂y₁)/(m₁ + m₂)

= (3×7 + 2×2)/(3+2)

= (21+4)/5

= 25/5

= 5

∴ Co-ordinates of P will be (4, 5)

Now equation of the line passing through P and having slope –1

y – y₁ = m(x – x₁)

⇒ y – 5 = -1(x – 4)

⇒ y – 5 = -x + 4

⇒ x + y – 5 – 4 = 0

⇒ x + y – 9 = 0

Question-12

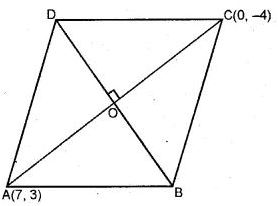
The points A (7, 3) and C (0, – 4) are two opposite vertices of a rhombus ABCD. Find the equation of the diagonal BD.

Answer-12

Slope of line AC (m₁)

= (y₂ – y₁)/(x₂ – x₁)

= (-4 – 3)/(0 – 7)

= -7/-7

= 1

∵ Diagonals of a rhombus bisect each other at right angles

∴ BD is perpendicular to AC

∴ Slope of BD = -1 (∵ m₁m₂ = -1)

And co-ordinates of O, the mid-point of AC will be {(7 + 0)/2, (3 – 4)/2} or (7/2, -1/2)

∴ Equation of BD will be

y – y₁ = m(x – x₁)

⇒ y + 1/2 = -1 (x – 7/2)

⇒ y + 1/2 = -x + 7/2

⇒ 2y + 1 = -2x + 7

⇒ 2x + 2y + 1 – 7 = 0

⇒ 2x + 2y – 6 = 0

⇒ x + y – 3 = 0 (Dividing by 2)

Question-13  

A straight line passes through P (2, 1) and cuts the axes in points A, B. If BP : PA = 3 : 1, find:

(i) the co-ordinates of A and B
(ii) the equation of the line AB

Answer-13

A lies on x-axis and B lies on y-axis
Let co-ordinates of A be (x, 0) and B be (0, y)
and P (2, 1) divides BA in the ratio 3 : 1.

∴ x = (m₁x₂ + m₂x₁)/(m₁ + m₂)

⇒ 2 = (3×x + 1×0)/(3+1)

⇒ 3x/4 = 2

⇒ 3x = 8

⇒ x = 8/3

And y = (m₁y₂ + m₂y₁)/(m₁ + m₂)

⇒ 1 = (3×0 + 1×y)/(3+1)

⇒ y/4 = 1

⇒ y = 4

∴ Co-ordinates of A will be (8/3, 0) and of B will be (0, 4)

(ii) Slope of the line AB = (y₂ – y₁)/(x₂ – x₁)

= (4 – 0)/(0 – 8/3)

= {4/(-8/3)}

= – 4 × 3/8

= -3/2

∴ Equation of AB will be

y – y₁ = m(x – x₁)

⇒ y – 1 = -3/2 (x – 2)

⇒ 2y – 2 = -3x + 6

⇒ 3x + 2y – 2 – 6 = 0

⇒ 3x + 2y – 8 = 0

Question-14

A straight line makes on the co-ordinates axes positive intercepts whose sum is 7. If the line passes through the point ( – 3, 8), find its equation.

Answer -14

Let the line make intercept a and b with the
x-axis and y-axis respectively then the line passes through

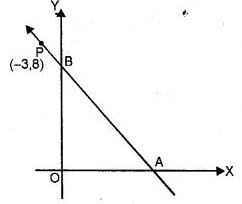
A (a, 0) and B (0, b)

But a + b = 7

b = 7 – a

Now slope of the line = (y₂ – y₁)/(x₂ – x₁)

= (b – 0)/(0 – a)

= -b/a

∴ Equation of the line y – y₁ = m(x – x₁)

⇒ y – 0 = (-b/a).(x – a) …(i)

∵ the line passes through the point (-3, 8)

∴ 8 – 0 = -b/a(- 3 – a)

= – {(7 – a)/a}×(-3 – a)

⇒ 8a = (7 – a)(3 + a)

⇒ 8a = 21 + 7a – 3a + a²

⇒ a² + 8a – 7a + 3a – 21 = 0

⇒ a² + 4a – 21 = 0

⇒ a² + 7a – 3a – 21 = 0

⇒ a(a + 7) – 3(a + 7) = 0

⇒ (a + 7)(a – 3) = 0

Either a + 7 = 0, then a = -7, which is not possible as it is not positive

Or a – 3 = 0, then a = 3

and b = 7 – 3 = 4

∴ Equation of the line y – 0 = -(b/a)×(x – a)

⇒ y = -4/3(x – 3)

⇒ 3y = -4x + 12

⇒ 4x + 3y – 12 = 0

⇒ 4x + 3y = 12

Hence, the equation of the line is x3+y4=1  or 4x + 3y = 12

Question-15  

If the coordinates of the vertex A of a square ABCD are (3, – 2) and the equation of diagonal BD is 3 x – 7 y + 6 = 0, find the equation of the diagonal AC. Also find the co-ordinates of the centre of the square.

Answer -15

Co-ordinates of A are (3, -2).

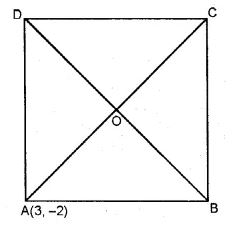
Diagonals AC and BD of the square ABCD
bisect each other at right angle at O.
∴ O is the mid-point of AC and BD Equation

Diagonals AC and BD of the square ABCD bisect each other at right angle at O.

∴ O is mid-point of AC and BD

Equation of BD is 3x – 7y + 6 = 0

⇒ 7y = 3x + 6

⇒ y = (3/7)×x + 6/7

∴ Slope of BD = 3/7

And slope of AC = -7/3 (∵ m₁m₂ = -1)

∴ Equation of AC will be

y – y₁ = m(x – x₁)

⇒ y + 2 = -7/3 (x – 3)

⇒ 3y + 6 = -7x + 21

⇒ 7x + 3y + 6 – 21 = 0

⇒ 7x + 3y – 15 = 0

Now we will find the co-ordinates of O, the points of intersection of AC and BD

We will solve the equations,

3x – 7y = – 6 …(i)

7x + 3y = 15 …(ii)

Multiplying (i) by 3 and (ii) by 7, we get,

9x – 21y = – 18 …(iii)

49x + 21y = 105 …(iv)

Adding we get,

58x = 87

⇒ x = 87/58 = 3/2

Substituting the value of x in (iii)

9(3/2) – 21y = – 18

⇒ 27/2 – 21y = – 18

21y = 27/2 + 18

= (27 + 36)/2

= 63/2

y = 63/(2×21)

= 3/2

∴ Co-ordinates of O will be (3/2, 3/2)

— : End ML Aggarwal Equation of Straight Line Ch-Test Class 10 ICSE :–

Return to :- ML Aggarwal Solutions for ICSE Class-10

Thanks

Please Share with Your Friends