ML Aggarwal Heights and Distances Chapter Test Solutions ICSE Class-10 Maths Ch-20

ML Aggarwal Heights and Distances Chapter Test Solutions ICSE Class-10 Maths Ch-20. We Provide Step by Step Answer of Chapter Test Heights and Distances Questions for ICSE Class-10 APC Understanding Mathematics. Visit official Website CISCE for detail information about ICSE Board Class-10.

ML Aggarwal Heights and Distances Chapter Test Solutions ICSE Class-10 Maths Ch-20

Board	ICSE
Subject	Maths
Class	10th
Chapter-20	Heights and Distances
Writer / Book	Understanding
Topics	Solutions of Chapter Test
Academic Session	2024-2025

Heights and Distances Chapter Test

ML Aggarwal Solutions ICSE Class-10 Maths Ch-20

Question 1. The angle of elevation of the top of a tower from a point A (on the ground) is 30°. On walking 50 m towards the tower, the angle of elevation is found to be 60°. Calculate

(i) the height of the tower (correct to one decimal place).
(ii) the distance of the tower from A.

Answer :

Let TR be the tower and A is a point on the ground
and angle of elevation of the top of tower = 30°
AB = 50 m
and from B, the angle of elevation is 60°
Let TR = h and AR = x
BR = x – 50

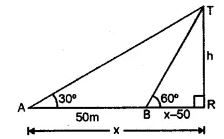
In right triangle ATR

tan θ = TR/AR

tan 30⁰ = h/x

1/√3 = h/x

⇒ x = √3h …(1)

In right triangle BTR

tan θ = TR/BR

tan 60⁰ = h/(x – 50)

√3 = h/(x – 50)

⇒ h = √3 (x – 50) …(2)

Using both the equations

⇒ h = √3 (√3h – 50)

h = 3h – 50√3

⇒ 2h = 50√3

⇒ h = 25 √3

h = 25 × 1.732 = 43.3

Now substituting the values of h in equation (1)

x = √3 × 25√3

⇒ x = 25 × 3

⇒ x = 75

Height of the tower = 43.3 m

Distance of A from the foot of the tower = 75 m

Question 2. An aeroplane 3000 m high passes vertically above another aeroplane at an instant when the angles of elevation of the two aeroplanes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the two planes.

Answer :

Let A and B are two aeroplanes
and P is a point on the ground such that
angles of elevations from A and B are 60° and 45° respectively.
AC = 3000 m
Let AB = x
∴ BC = 3000 – x
Let PC = y

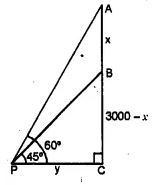
In right triangle APC

tan θ = AC/PC

tan 60⁰ = 3000/y

√3 = 3000/y

⇒ y = 3000/√3 …(1)

In right triangle BPC

tan θ = BC/PC

tan 45⁰ = (3000 – x)/y

1 = (3000 – x)/ y

⇒ y = 3000 – x

Using equation (1)

3000/√3 = 3000 – x

x = 3000 – 3000/√3

Multiply and divide by √3

x = 3000 – (3000 × √3)/(√3× √3)

So we get

x = 3000 – 1000 (1.732)

⇒ x = 3000 – 1732

⇒ x = 1268 m

Question 3. A 7m long flagstaff is fixed on the top of a tower. From a point on the ground, the angles of elevation of the top and bottom of the flagstaff are 45° and 36° respectively. Find the height of the tower correct to one place of demical.

Answer :

Let TR be the tower and PT is the flag on it such that PT = 7m
Let TR = h and AR = x
Angles of elevation from P and T are 45° and 36° respectively.
Now in right ∆PAR

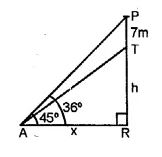
tan θ = PR/AR

tan 45⁰ = (7 + h)/x

1 = (7 + h)/x

⇒ x = 7 + h …(1)

In right triangle TAR

tan θ = TR/AR

tan 36⁰ = h/

0.7265 = h/x

⇒ h = x (0.7265) …(2)

Using both the equations

h = (7 + h) (0.7265)

h = 7 × 0.7265 + 0.7265h

⇒ h – 0.7265h = 7 × 0.7265

0.2735h = 7 × 0.7265

By division

h = (7 × 0.7265)/0.2735

h = (7 × 7265)/2735

⇒ h = 18.59 = 18.6 m

Question 4. A boy 1.6 m tall is 20 m away from a tower and observes that the angle of elevation of the top of the tower is 60°. Find the height of the tower.

Answer :

Let AB be the boy and TR be the tower
∴ AB = 1.6 m
Let TR = h
from A, show AE || BR
∴ ER = AB = 1.6 m
TE = h – 1.6
AE = BR = 20 m

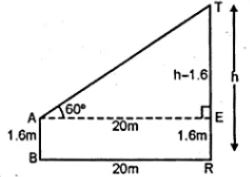
In right triangle TAE

tan θ = TE/AE

Substituting the values

tan 60⁰ = (h – 1.6)/20

So we get

√3 = (h – 1.6)/20

⇒ h – 1.6 = 20√3

⇒ h = 20√3 + 1.6

⇒ h = 20 (1.732) + 1.6

By further calculation

h = 34.640 + 1.6

h = 36.24
∴ Height of tower = 36.24 m

Question 5. A boy 1.54 m tall can just see the sun over a wall 3.64 m high which is 2.1 m away from him. Find the angle of elevation of the sun.

Answer :

Let AB be the boy and CD be the wall which is at a distance of 2.1 m

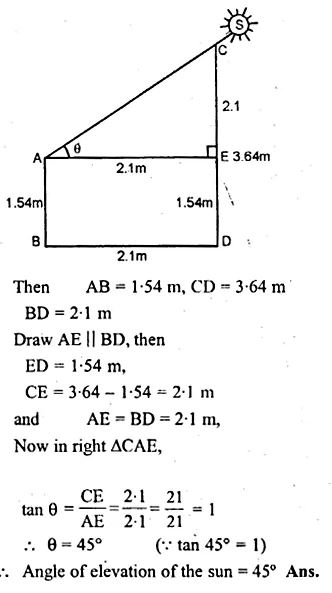
Hence, the angle of elevation of the sun is 45⁰.

Question 6. An aeroplane is flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.

Answer :

A and D are the two positions of the aeroplane ;
AB is the height and P is the point
∴ AB = 1 km,
Let AD = x and PB = y
and angles of elevation from A and D at point P are 60° and 30° respectively.

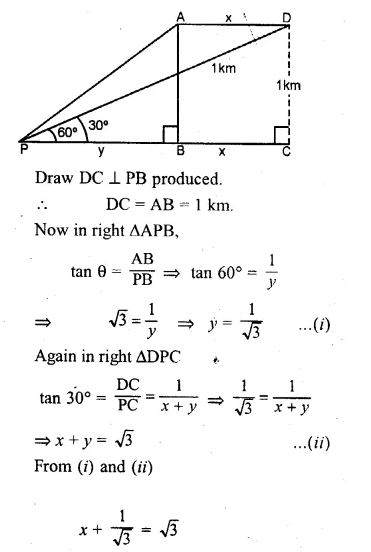
x = √3 – 1/√3

⇒ x = (3 – 1)/√3

⇒ x = 2/√3

Multiply and divide by √3

x = (2 × √3)/(√3 × √3)

x = (2 × 1.732)/3

⇒ x = 3.464/3 km

This distance is covered in 10 seconds

Speed of aeroplane (in km/hr) = 3.464/3 × (60 × 60)/10

= 3464/(3×1000) × 3600/10

= (3646 × 36)/300

= (3464 × 12)/100

= 41568/ 100

= 415.68 km/hr

Question 7. A man on the deck of a ship is 16 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 30°. Calculate the distance of the cliff from the ship and the height of the cliff.

Answer :

Let A is the man on the deck of a ship B and CE is the cliff.
AB = 16 m and angle of elevation from the top of the cliff in 45°and the angle of depression at the base of the cliff is 30°.
Let CE = h, AD = x, then
CD = h – 16, AD = BE = x
Now in right ∆CAD

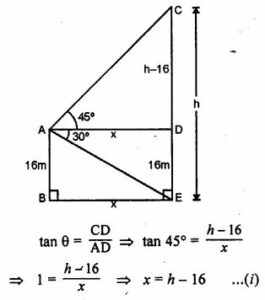
In right triangle ADE

tan θ = DE/AD

tan 30⁰ = 16/x

1/√3 = 16/x

⇒ x = 16√3 …(2)

Using both the equations

h – 16 = 16 √3

⇒ h = 16√3 + 16

Taking out the common terms

h = 16 (1.732 + 1)

⇒ h = 16 (2.732)

⇒ h = 43.712 = 43.71 m

x = h – 16

⇒ x = 43.71 – 16

⇒ x = 27.71

Distance of cliff = 27.71 m

Height of cliff = 43.71

Question 8. There is a small island in between a river 100 metres wide. A tall tree stands on the island. P and Q are points directly opposite to each other on the two banks and in the line with the tree. If the angles of elevation of the top of the tree from P and Q are 30° and 45° respectively, find the height of the tree.

Answer :

The width of the river (PQ) = 100 m.
B is the island and AB is the tree on it.

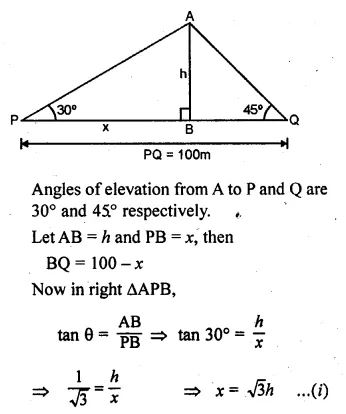
In right triangle ABQ

tan θ = AB/BQ

tan 45⁰ = h/(100 – x)

1 = h/(100 – x)

⇒ h = 100 – x …(2)

Using both the equations

h = 100 – √3h

h + √3h = 100

(1 + 1.732) h = 100

⇒ h = 100/2.732

Multiply and divide by 1000

h = (100 × 1000)/2732

⇒ h = 100000/2732

⇒ h = 36.6

Question 9. A man standing on the deck of the ship which is 20 m above the sea-level, observes the angle of elevation of a bird as 30° and the angle of depression of its reflection in the sea as 60°. Find the height of the bird

Answer :

Let P is the man standing on the deck of a ship
which is 20 m above the sea level and B is the bird.
Now angle of elevation of the bird from P = 30°
and angle of depression from P to the shadow of the bird in the sea  = 60⁰

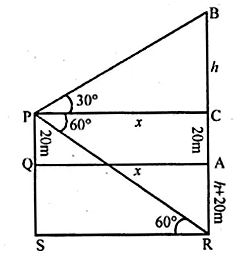
Let BC = h

PQ = 20 m = CA

AR = (h + 20) m

CE = h + 20 + 20 = h + 40 m

PC = CA = x

In right triangle PCB

tan 30⁰ = BC/PC

1/ √3 = h/x

x = √3h m …(1)

In right triangle PCR

tan 60⁰ = CR/PC

√3 = (h + 40)/ x

Using equation (1)

(h + 40)/√3h = √3

⇒ h + 40 = √3 × √3h = 3h

3h – h = 40

⇒ 2h = 40

⇒ h = 40/2 = 20

From the sea level the height of the bird = 20 + h = 20 + 20 = 40 m

—  : End of ML Aggarwal Heights and Distances Chapter Test Solutions ICSE Class-10 Maths Ch-20 : –

Return to :- ML Aggarwal Solutions for ICSE Class-10

Thanks

Please Share with Your Friends