ML Aggarwal Simultaneous Linear Equations Chapter Test Class 9 ICSE Maths Solutions. Step by step solutions of Simultaneous Linear Equations Ch-Test problems as council prescribe guideline. Visit official website CISCE for detail information about ICSE Board Class-9.
ML Aggarwal Simultaneous Linear Equations Chapter Test Class 9 ICSE Maths Solutions
| Board | ICSE |
| Subject | Maths |
| Class | 9th |
| Chapter-5 | Simultaneous Linear Equations |
| Topics | Solution of Ch-Test Questions |
| Academic Session | 2024-2025 |
Solution of Ch-Test Questions
ML Aggarwal Simultaneous Linear Equations Chapter Test Class 9 ICSE Maths Solutions
Solve the following simultaneous linear equations (1 to 4):
Question 1.
(i) 2x – (¾)y = 3,
5x – 2y = 7
(ii) 2(x-4) = 9y+2
x – 6y = 2
Answer :
(i) 2x-(3y/4)=3
(8x-3y)/4=3
8x-3y = 12 …(i)
5x-2y = 7 …(ii)
Multiply (i) by 5 and (ii) by 8, we get
40x-15y = 60 (iii)
40x -16y = 56 (iv)
Subtract (iv) from (iii), we get
y = 4
Substitute y in (i)
8x-3×4 = 12
8x = 12+12
8x = 24
x = 24/8
x = 3
Hence x = 3 and y = 4.
(ii) 2(x-4) = 9y+2
x – 6y = 2
2(x-4) = 9y+2
2x-8 = 9y+2
2x-9y = 2+8
2x-9y = 10 ….(i)
x-6y = 2 ….(ii)
Multiply (ii) by 2, we get
2x -12y = 4 ….(iii)
Subtract (iii) from (i), we get
2x-9y = 10
-2x +12y = -4
0+3y = 6
3y = 6
y = 6/3
y = 2
Substitute the value of y in (i)
2x-9×2 = 10
2x-18 = 10
2x = 10+18
2x = 28
x = 28/2
x = 14
Hence x = 14 and y = 2.
Question 2.
(i) 97x+53y = 177
53x+97y = 573
(ii) x+y = 5.5
x-y = 0.9
Answer :
Given equations are as follows.
(i) 97x+53y = 177 …(i)
53x+97y = 573 …(ii)
Multiply (i) by 53 and (ii) by 97
53(97x+53y) = 53×177
5141x+2809y = 9381 …..(iii)
97(53x+97y) = 97×573
5141x+9409y = 55581 …..(iv)
Subtract (iv) from (iii)
5141x+2809y = 9381 …..(iii)
5141x+9409y = 55581 …..(iv)
——————————
0x -6600y = -46200
-6600y = -46200
y = -46200/-6600
y = 7
Substitute the value of y in (i)
97x+53×7 = 177
97x+371 = 177
97x = 177-371
97x = – 194
x = -194/97
x = -2
Hence x = -2 and y = 7.
(ii) x+y = 5.5
x-y = 0.9
x+y = 5.5 …(i)
x-y = 0.9 …(ii)
——————–
Adding (i) and (ii), we get
2x = 5.5+0.9
2x = 6.4
x = 6.4/2
x = 3.2
Substitute value of x in (i)
3.2+y = 5.5
y = 5.5-3.2
y = 2.3
Hence x = 3.2 and y = 2.3.
Question 3.
(i) x+y = 7xy
2x-3y+xy = 0
(ii) 30/(x-y) …….
Answer :
(i) x+y = 7xy …(i)
2x-3y+xy = 0 …..(ii)
Divide (i) by xy, we get
(x/xy)+(y/xy)=7xy/xy
(1/y)+(1/x)=7……(iii)
Divide (ii) by xy, we get
(2x/xy) -(3y/xy)+(xy/xy)=0
(2/y)-(3/x)+1=0
(-3/x)+(2/y)=-1…….(iv)
Multiplying (iii) by 3, we get
(3/x)+(3/y)=3×7
(3/x)+(3/y)=21……..(v)
Adding (v) and (iv), we get
5/y=20
y=5/20
y=1/4
Substitute value of y in (iv)
(-3/x)+2×4=-1
(-3/x)+8=-1
(-3/x)=-1-8
-3/x=-9
x=3/9
x=1/3
Hence x = 1/3 and y = 1/4.
(ii)

Substitute (v) in (i), we get
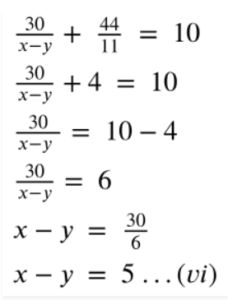
Now solve for (v) and (vi)
x+y = 11
x-y = 5
Add (v) and (vi)
2x = 16
x = 16/2 = 8
Substitute x in (v)
8+y = 11
y = 11-8
y = 3
Hence x = 8 and y = 3.
Question 4.
(i) ax+by = a-b
bx-ay = a+b
(ii) 3x + 2y = 2xy
(1/x)+(2/y)=7/6
Answer :
(i) ax+by = a-b …(i)
bx-ay = a+b …(ii)
multiplying (i) by a and (ii) by b, we get
a(ax+by) = a(a-b)
a2x +aby = a2-ab …(iii)
b(bx-ay) = b(a+b)
b2x -aby = ab+b2 …(iv)
Adding (iii) and (iv)
a2x +aby = a2-ab
b2x -aby = ab+b2
———————–
(a2+b2)x = (a2+b2)
x = (a2+b2)/ (a2+b2)
x = 1
Substitute the value of x in (i), we get
a×1+by = a-b
a+by = a-b
by = -b
y = -b/b
y = -1
Hence x = 1 and y = -1.
(ii) 3x + 2y = 2xy
(1/x)+(2/y)=7/6
3x + 2y = 2xy …(i)
(1/x)+(2/y)=7/6….(ii)
Divide (i) by xy
(3x/xy)+(2y/xy)=2xy/xy
(3/y)+(2/x)=2……..(iii)
Multiply (ii) by 2, we get
(2/x)+(4/y)=7/3……(iv)
Subtract (iii) from (iv)
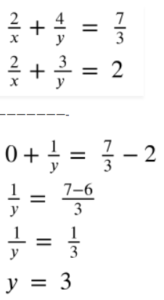
Substitute y in (iii)
(3/3) + (2/x) = 2
1+(2/x) = 2
(2/x) = 1
x = 2
Hence x = 2 and y = 3.
Question 5. Solve 2x -(3/y) =9, 3x + (7/y) = 2. Hence find the value of k if x = ky + 5.
Answer :
2x -(3/y) = 9 …(i)
3x + (7/y) = 2 …(ii)
Multiply (i) by 3 and (ii) by 2, we get
6x-(9/y) = 27 ..(iii)
6x+(14/y) = 4 …(iv)
Subtracting (iv) from (iii), we get
-23/y = 23
y = 23/-23
y = -1
Substitute y in (i)
2x-(3/-1) = 9
2x+3 = 9
2x = 9-3
2x = 6
x = 6/2
x = 3
Hence x = 3 and y = -1.
Given x = ky+5
Substitute x and y in above eqn
3 = k×-1+5
3 = -k+5
k = 5-3
k = 2
Hence the value of k is 2.
Question 6. Solve, 1/(x+y)-1/2x=1/30, 5/(x+y)+1/3=4/3 Hence find the value of 2x2-y2.
Answer :
1/(x+y)-1/2x=1/30….(i)
5/(x+y)+1/3=4/3………(ii)
Let (x+y) = a
(1/a)-(1/2x)
1/a-1/2x=1/30……(iii)
5/a+1/x=4/3
Multiply (iii) by 5
5/a – 5/2x=1/6………(iv)
5/a + 1/x=4/3
Subtracting (ii) from (iv)
(-5/2x) -1/x=1/6 – 4/3
(-5-2)/2x=(1-8)/6
-7/2x =-7/6
2x =6
x=3
Substitute x in (iii)
(1/a) -1/(2×3) = 1/30
(1/a) – (1/6) = 1/30
1/a = (1/30)+(1/6)
1/a = (1+5)/30
1/a = 6/30
a = 30/6
a = 5
Substitute a in x+y = a
3+y = 5
y = 5-3
y = 2
Hence x = 3, y = 2.
2x2-y2 = 2×32-22
= 2×9-4
= 18-4
= 14
Hence the value of 2x2-y2 is 14.
Question 7. Can x, y be found to satisfy the following equations simultaneously ?
(2/y)+(5/x)=19
(5/y)-(3/x)=1
3x+8y=5
If so, find them.
Answer :
(2/y)+(5/x)=19…….(i)
(5/y)-(3/x)=1………..(ii)
3x+8y=5……..(iii)
Multiply (i) by 5 and (ii) by 2, we get
(10/y) +(25/x)=95……(iv)
(10/y)-6/x =2…….(v)
Subtract (v) from (iv)
31/x = 95-2
31/x = 93
x = 31/93
x = 1/3
Substitute x in (i)
(2/y)+5÷(1/3) = 19
(2/y)+5×3 = 19
(2/y) = 19-15
(2/y) = 4
y = 2/4
y = 1/2
Substitute x and y in (iii)
3×(1/3) + 8×(1/2) = 5
1+4 = 5
The value of x and y satisfies (iii).
Hence the given equations are simultaneous.
— : End of ML Aggarwal Simultaneous Linear Equations Chapter Test Class 9 ICSE Maths Solutions :–
Return to :- ML Aggarawal Maths Solutions for ICSE Class-9
Thanks
Please Share with Your Friends


