ML Aggarwal Rectilinear Figures Chapter Test Class 9 ICSE Maths Solutions

ML Aggarwal Rectilinear Figures Chapter Test Class 9 ICSE Maths Solutions Ch-13. Step by Step Solutions of Ch-Test questions on Rectilinear Figures of ML Aggarwal for ICSE Class 9th Mathematics. Visit official website CISCE for detail information about ICSE Board Class-9.

ML Aggarwal Rectilinear Figures Chapter Test Class 9 ICSE Maths Solutions

Board	ICSE
Subject	Maths
Class	9th
Chapter-13	Rectilinear Figures
Topics	Solution of Ch-Test Questions
Academic Session	2024-2025

Chapter Test Questions with Solutions on Rectilinear Figures

ML Aggarwal Rectilinear Figures Chapter Test Class 9 ICSE Maths Solutions Ch-13

Question 1. In the given figure, ABCD is a parallelogram. CB is produced to E such that BE=BC. Prove that AEBD is a parallelogram.

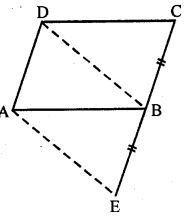
Answer :  ABCD is a || gm in which CB is produced to E such that BE = BC

BD and AE are joined

To prove:  AEBD is a parallelogram

Proof: In ∆AEB and ∆BDC

EB = BC [Given]

∠ABE = ∠DCB [Corresponding angles]

AB = DC [Opposite sides of ||gm]

Thus, ∆AEB ≅ ∆BDC by S.A.S axiom

So, by C.P.C.T

But, AD = CB = BE [Given]

As the opposite sides are equal and ∠AEB = ∠DBC

But these are corresponding angles

Therefore, AEBD is a parallelogram.

Question 2. In the given figure, ABC is an isosceles triangle in which AB=AC. AD bisects exterior angle PAC and CD || BA. Show that

(i) ∠DAC=∠BCA
(ii) ABCD is a parallelogram.

Answer : In isosceles triangle ABC, AB = AC. AD is the bisector of ext. ∠PAC and CD || BA

To prove:  (i) ∠DAC = ∠BCA

(ii) ABCD is a || gm

Proof: In ∆ABC

AB = AC [Given]

∠C = ∠B

Since, ext. ∠PAC = ∠B + ∠C

= ∠C + ∠C

= 2 ∠C

= 2 ∠BCA

So, ∠DAC = 2 ∠BCA

∠DAC = ∠BCA

Thus, AD || BC

But, AB || AC

Therefore, ABCD is a || gm.

Question 3. Prove that the quadrilateral obtained by joining the mid-points of an isosceles trapezium is a rhombus.

Answer : ABCD is an isosceles trapezium in which AB || DC and AD = BC

P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively PQ, QR, RS and SP are joined.

To prove:  PQRS is a rhombus

Construction:  Join AC and BD

Proof: ABCD is an isosceles trapezium

Its diagonals are equal

AC = BD

in ∆ABC

P and Q are the mid-points of AB and BC

PQ || AC and PQ = ½ AC …(i)

in ∆ADC

S and R mid-point of CD and AD

So, SR || AC and SR = ½ AC …(ii)

From (i) and (ii), we have

PQ || SR and PQ = SR

PQRS is a parallelogram.

Now, in ∆APS and ∆BPQ

AP = BP [P is the mid-point]

AS = BQ [Half of equal sides]

∠A = ∠B [As ABCD is an isosceles trapezium]

So, ∆APS ≅ ∆BPQ by SAS Axiom of congruency

by C.P.C.T we have

PS = PQ

But there are the adjacent sides of a parallelogram

So, sides of PQRS are equal

Hence, PQRS is a rhombus

Question 4. Find the size of each lettered angle in the Following Figures.

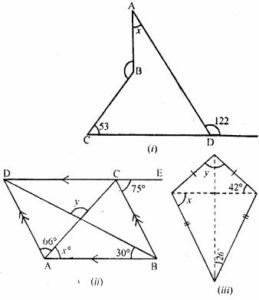
Answer : (i) As CDE is a straight line

∠ADE + ∠ADC = 180^o

⇒ 122^o + ∠ADC = 180^o

⇒ ∠ADC = 180^o – 122^o = 58^o …(i)

⇒ ∠ABC = 360^o – 140^o = 220^o …(ii) (At any point the angle is 360^o)

∠ADC + ∠BCD + ∠BAD + ∠ABC = 360^o

⇒ 58^o + 53^o + x + 220^o = 360^o (Using (i) and (ii))

⇒ 331^o + x = 360^o

⇒ x = 360^o – 331^o

⇒ x = 29^o

(ii) As DE || AB

∠ECB = ∠CBA (Alternate angls])

⇒ 75^o = ∠CBA

⇒ ∠CBA = 75^o

Since, AD || BC we have

(x + 66^o) + 75^o = 180^o

⇒ x + 141^o = 180^o

⇒ x = 180^o – 141^o

⇒ x = 39^o …(i)

in ∆AMB

x + 30^o + ∠AMB = 180^o (Angles sum property of a triangle)

⇒ 39^o + 30^o + ∠AMB = 180^o [From (i)]

⇒ 69^o + ∠AMB + 180^o

⇒ ∠AMB = 180^o – 69^o = 111^o …(ii)

Since, ∠AMB = y

⇒ y = 111^o

Hence, x = 39^o and y = 111^o

(iii) In ∆ABD

AB = AD [Given]

∠ABD = ∠ADB

⇒ ∠ABD = 42^o (Since, given ∠ADB = 42^o)

∠ABD + ∠ADB + ∠BAD = 180^o (Angles sum property of a triangle)

⇒ 42^o + 42^o + y = 180^o

⇒ 84^o + y = 180^o

⇒ y = 180^o – 84^o

⇒ y = 96^o

⇒ ∠BCD = 2 ×26^o = 52^o

In ∆BCD,

As BC = CD

∠CBD = ∠CDB = x

∠CBD + ∠CDB + ∠BCD = 180^o

⇒ x + x + 52^o = 180^o

⇒ 2x + 52^o = 180^o

⇒ 2x = 180^o – 52^o

⇒ x = 128^o/2

⇒ x = 64^o

Therefore, x = 64^o and y = 90^o.

Question 5. Find the size of each lettered angle in the following figures :

Answer :  (i) AB || CD and BC || AD

ABCD is a || gm

y = 2× ∠ABD

⇒ y = 2× 53^o = 106^o …(1)

Also, y + ∠DAB = 180^o

⇒ ∠DAB = 180^o – 106^o

= 74^o

x = ½ ∠DAB (As AC bisects ∠DAB)

x = ½ × 74^o = 37^o

and ∠DAC = x = 37^o …(ii)

Also, ∠DAC = z …(iii) (Alternate angles)

From (ii) and (iii), z = 37^o 

Hence, x = 37^o, y = 106^o and z = 37^o

(ii) As ED is a straight line, we have

60^o + ∠AED = 180^o

⇒ ∠AED = 180^o – 60^o

⇒ ∠AED = 120^o …(i)

as CD is a straight line

50^o + ∠BCD = 180^o

⇒ ∠BCD = 180^o – 50^o

⇒ ∠BCD = 130^o …(ii)

In pentagon ABCDE, we have

∠A + ∠B+ ∠AED + ∠BCD + ∠x = 540^o (Sum of interior angles in pentagon is 540^o)

⇒ 90^o + 90^o 120^o + 130^o + x = 540^o

⇒ 430^o + x = 540^o

⇒ x = 540^o – 430^o

⇒ x = 110^o

Hence,  value of x = 110^o

(iii) In given figure, AD || BC

60^o + y = 180^o and x + 110^o = 180^o

⇒ y = 180^o – 60^o and x = 180^o – 110^o

⇒ y = 120^o and x = 70^o

CD || AF

∠FAD = 70^o …(i)

In quadrilateral ADEF,

∠FAD + 75^o + z + 130^o = 360^o

⇒ 70^o + 75^o + z + 130^o = 360^o

⇒ 275^o + z = 360^o

⇒ z = 360^o – 275^o = 85^o

Therefore,  x = 70^o, y = 120^o and z = 85^o

Question 6. In the adjoining figure, ABCD is a rhombus and DCFE is a square. If ∠ABC = 56°, find

(i) ∠DAG
(ii) ∠FEG
(iii) ∠GAC
(iv) ∠AGC.

Answer :

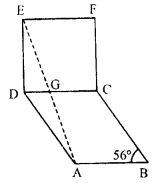
AB = BC = DC = AD …(i)

DC = EF = FC = EF …(ii)

From (i) and (ii), we have

AB = BC = DC = AD = EF = FC = EF …(iii)

∠ABC = 56^o

∠ADC = 56^o (Opposite angle in rhombus are equal)

So, ∠EDA = ∠EDC + ∠ADC = 90^o + 56^o = 146^o

In ∆ADE,  DE = AD (From (iii))

∠DEA = ∠DAE (Equal sides have equal opposite angles)

∠DEA = ∠DAG = (180^o – ∠EDA)/2

= (180^o – 146^o)/2

= 34^o/2

= 17^o

⇒ ∠DAG = 17^o

Also, ∠DEG = 17^o

∠FEG = ∠E – ∠DEG

= 90^o – 17^o

= 73^o

In rhombus ABCD,

∠DAB = 180^o – 56^o = 124^o

⇒ ∠DAC = 124^o/2 (Since, AC diagonals bisect the ∠A)

⇒ ∠DAC = 62^o

∠GAC = ∠DAC – ∠DAG

= 62^o – 17^o

= 45^o

In ∆EDG,  ∠D + ∠DEG + ∠DGE = 180^o

⇒ 90^o + 17^o + ∠DGE = 180^o

⇒ ∠DGE = 180^o – 107^o = 73^o …(iv)

∠AGC = ∠DGE …(v) (Vertically opposite angles)

Therefore, from (iv) and (v), we have

∠AGC = 73^o

Question 7. If one angle of a rhombus is 60° and the length of a side is 8 cm, find the lengths of its diagonals.

Answer :  Each side of rhombus ABCD is 8cm

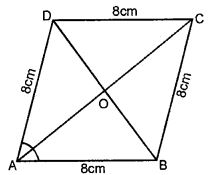
AB = BC = CD = DA = 8cm

Let ∠A = 60^o

∆ABD is an equilateral triangle

Then, AB = BD = AD = 8cm

the diagonals of a rhombus bisect each other at right angles

AO = OC, BO = OD = 4 cm and ∠AOB = 90^o

in right ∆AOB

AB² = AO² + OB²

⇒ 8² = AO² + 4²

⇒ 64 = AO² + 16

⇒ AO² = 64 – 16 = 48

⇒ AO = √48 = 4√3cm

AC = 2 AO

Therefore,  AC = 2 × 4√3 = 8√3cm.

Question 8. Using ruler and compasses only, construct a parallelogram ABCD with AB = 5 cm, AD = 2.5 cm and ∠BAD = 45°. If the bisector of ∠BAD meets DC at E, prove that ∠AEB is a right angle.

Answer :   Construction:

(i) Draw AB = 5.0cm

 

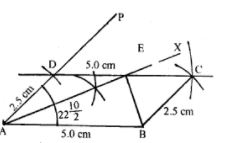
(ii) Draw BAP = 45^o on side AB

(iii) Take A as centre and radius 2.5cm cut the line AP at D

(iv) Take D as centre and radius 5.0cm draw an arc

(v) Take B as centre and radius equal to 2.5cm cut the arc of step (iv) at C

(vi) Join BC and CD

(vii) ABCD is the required parallelogram

(viii) Draw the bisector of ∠BAD, which cuts the DC at E

(ix) Join EB

(x) Measure ∠AEB which is equal to 90^o.

—  : End of ML Aggarwal Rectilinear Figures Chapter Test Class 9 ICSE Maths Solutions :–

Return to :-  ML Aggarawal Maths Solutions for ICSE  Class-9

Thanks

Please Share with Your Friends