ML Aggarwal Theorems on Area Chapter Test Class 9 ICSE Maths Solutions Ch-14. Step by Step Solutions of Chapter Test Questions on Theorems on Area of ML Aggarwal for ICSE Class 9th Mathematics. Visit official website CISCE for detail information about ICSE Board Class-9.
ML Aggarwal Theorems on Area Chapter Test Class 9 ICSE Maths Solutions
| Board | ICSE |
| Subject | Maths |
| Class | 9th |
| Chapter-14 | Theorems on Area |
| Topics | Solution of Ch-Test Questions |
| Academic Session | 2024-2025 |
Solution of Ch-Test Questions on Theorems on Area
ML Aggarwal Theorems on Area Chapter Test Class 9 ICSE Maths Solutions Ch-14
Question 1.
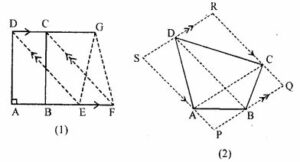
(a) In the figure (1) given below, ABCD is a rectangle (not drawn to scale ) with side AB = 4 cm and AD = 6 cm. Find :
(i) the area of parallelogram DEFC
(ii) area of ∆EFG.
(b) In the figure (2) given below, PQRS is a parallelogram formed by drawing lines parallel to the diagonals of a quadrilateral ABCD through its corners. Prove that area of || gm PQRS = 2 x area of quad. ABCD.
Answer :
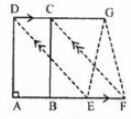
(a)Given. ABCD is a rectangle AB = 4 cm and AD = 6 cm.
D C cm and AD = 6 cm.
Required. (i) The area of || gm DEFC.
(ii) area of ∆ EFG
(i) Since AB = 4cm and AD = 6 cm (given)
∴ Area of rectangle ABCD = AB × AD
= 4 cm × 6 cm = 24 cm2
area of rectangle ABCD = area of || gm DEFC (∵ Both are on the same Base and between the same parallel lines)
⇒ Area of || gm DEFC = 24 cm2
(ii) Area of ∆EFG = 1/2 (area of || gm DEFC)
(∴ Both are on the same base and between the same parallel lines)
∴ Area of AEFG = (1/2)7 × 24 cm2 =12 cm2
(b) Given. PQRS is a || gm formed by drawing lines parallel to the diagonals of quadrilateral ABCD through its comers.
To prove. Area of II gm PQRS = 2. area of quad. ABCD
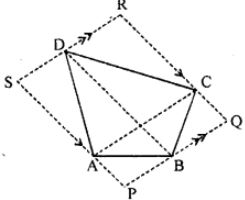
Proof. ar(∆ACD) = 1/2 ar(|| gm ACRS)
[∴ both are on same base AC and between the same || AC and SR ]
⇒ ar (|| gm ACRS) = 2ar(∆ACD) …….(1)
ar ( ∆ ABC) = 1/2ar (|| gm ∆APQC)
⇒ ar (|| gm APQC) = 2ar ( ∆ ABC) …..(2)
Adding (1) from (2),
ar (|| gm ACRS) + ar (|| gm APQC) = 2ar(∆ACD) + 2ar (∆ABC)
⇒ (|| gm PQRS) = 2[ar (∆ ACD) + ar ( ∆ ABC)]
⇒ ar (|| gm PQRS) = 2ar (quad. ABCD)
Question 2. In the parallelogram ABCD, P is a point on the side AB and Q is a point on the side BC. Prove that
(i) area of ∆CPD = area of ∆AQD
(ii)area of ∆ADQ = area of ∆APD + area of ∆CPB.
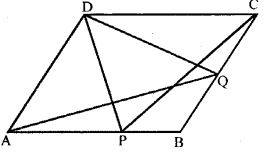
Answer :
Given. || gm ABCD in which P is a point on AB and Q is a point on BC.
To prove. (i) ar (∆ CPD) = ar ( ∆ AQD)
(ii) ar (∆ ADQ) = ar ( ∆ APD) + ar (∆ CPB)
Proof. ∆ CPD and II gm ABCD are on the same base CD and between the same parallels lines AB and CD.
∴ ar (∆ CPD) = 1/2 ar (|| gm ABCD) …..(1)
∆ ADQ and || gm ABCD are on the same base AD and between the same II lines AD and BC,
ar ( ∆ ADQ) = 1/2 (|| gm ABCD) ………(2)
From (1) and (2),
ar ( ∆ CPD) = ar( ∆ ADQ)
or ar ( ∆ CPD) = ar (∆ ADQ) (Q.E.D.)
(ii) ar (∆ ADQ) = 1/2 ar (|| gm ABCD) ( Proved in part (i) above )
⇒ 2ar (∆ ADQ) = ar (|| gm ABCD)
⇒ ar (∆ ADQ) + ar( ∆ ADQ) = ar (|| gm ABCD) ……..(3)
But ar ( ∆ ADQ) = ar (∆ CPD) …………(4)
(Proved in part (i) above)
From (3) and (4),
ar ( ∆ ADQ) + ar ( ∆ CPD) = ar (|| gm ABCD)
⇒ ar ( ∆ ADQ) + ar ( ∆ CPD)
⇒ ar (∆ APD) + ar (∆ CPD) + ar (∆ CPB)
⇒ or (∆ ADQ) = ar( ∆ APD) + ar (∆ CPB) (Q.E.D.)
Question 3. In the adjoining figure, X and Y are points on the side LN of triangle LMN. Through X, a line is drawn parallel to LM to meet MN at Z. Prove that area of ∆LZY = area of quad. MZYX.

Answer :
In the figure,
X and Y are points on side LN of ALMN.
Through X, a line XZ || LM is drawn which meets MN at Z.
To prove : area of ∆LZY = area of quad. MZYX
Join MX, ZY and LZ
Proof: ∆ LM || XZ
and ∆LZX and ∆MZX are on the same base XZ and between the same parallels
∴ area ∆LZX = area ∆MZX
Adding area ∆XZY to both sides area ∆LZX + area ∆XZY
= area ∆MZX + area ∆XZY
⇒ area ∆LZY = area quadrilateral MZYX
Question 4. Perpendiculars are drawn from a point within an equilateral triangle to the three sides. Prove that the sum of the three perpendiculars is equal to the altitude of the triangle.
Answer :
ABC is an equilateral triangle, i.e. AB = BC = CA. P is any point within an equilateral triangle to the three sides.
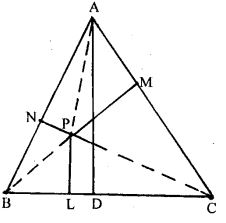
PN, PM, and PL are perpendicular on side AB, AC and BC respectively. AD is any altitude from point A on side BC.
Prove. AD = NP + LP + MP
Join PA, PB and PC.
Proof. Area of ∆ ABC = 1/2 × Base × Altitude
or(∆ABC)= 1/2 × BC × AD ………(1)
area of ∆ APB = 1/2 × AB × NP ………….(2)
area of ∆ APC = 1/2 × AC × MP
area of ∆ BPC = 1/2 × BC × LP …….(4)
Adding (2), (3) and (4)
ar ( ∆ APB) + ar (∆ APC) + ar (∆ BPC)
= 1/2 × AB × NP + 1/2 × AC × MP + 1/2 × BC × LP
ar(∆ ABC) = 1/2 [AB × NP + AC × MP × BC × LP]
= 1/2 [BC × NP + BC MP × BC × LP] (∵ Ab = AC = CA)
ar(∆ABC) = 1/2 × BC[NP + MP + LP ] ..(5)
From (4) and (5),
1/2 × BC × AD = 1/2 × BC × (NP + LP + MP)
⇒ AD = NP + LP + MP
⇒ NP + LP + MP = AD
Question 5. If each diagonal of a quadrilateral’ divides it into two triangles of equal areas, then prove that the quadrilateral is a parallelogram.
Answer : ar (∆ ABC) = ar (∆ ADC) given
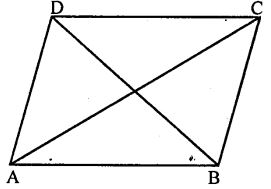
To prove : ABCD is a parallelogram.
Join BD.
Proof: ∵ Diagonals of quad. ABCD divides the quad, into two triangles of equal area.
∴ ar( ∆ ABC) = ar( ∆ ABD)
= 1/2 ar (ABCD)
But, these are on the same base AB
∴ Their heights are equal
∴ DC || AB …(i)
prove that : ar (∆ABC) = ar (∆BDC)
∴ BC || AD …(ii)
From (i) and (ii)
ABCD is a parallelogram.
Hence proved.
Question 6. In the given figure, ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F. If area of ∆DFB = 3 cm², find the area of parallelogram ABCD.
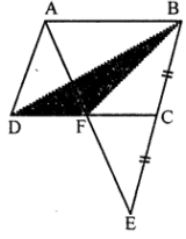
Answer : In the given figure,
ABCD is a parallelogram BC is produced to E such that CE = BC
Join BD and AE, DC at F
Join BF, AC and DE
∴ Area of ∆DFB = 3 cm2
Find the area of ||gm ABCD
∵ In ∆ABE, C is mid-point of BE and CD || AB
∴ F is mid-point of AE and CD
∴ ABED is a ||gm (∵ Diagonals AE and CD bisect each other at F)
∵ BD is the diagonal of ||gm ABCD
∆BCD = 1/2 ||gm ABCD
∵ F is mid-point of DC
∴ ADFB = 1/2 ∆BCD
⇒ ADFB = 1/2 × 1/2 (||gm ABCD)
⇒ ADFB = 1/2 (||gm ABCD)
∴ area ||gm ABCD = 4 area ∆DFB
= 4 × 3 = 12 cm2
Question 7. In the given figure, ABCD is a square. E and F are mid-points of sides BC and CD respectively. If R is mid-point of EF, prove that: area of ∆AER = area of ∆AFR.
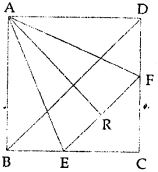
Answer : In square ABCD, BD is diagonals E and F are mid-point of BC and CD respectively.
R is mid-point of EF.
To prove : area (∆AER = area (∆AFR)
Proof: In ∆ABE and ∆ADF
AB = AD (Sides of a square)
∠B = ∠D (Each 90°)
BE = CE (E is mid-point of BC)
∴ ∆ABE ≅ ∆ADF (SAS axiom)
∴ AE = AF (c.p.c.t.)
Again in ∆AER and ∆AFR
AE = AF (Produced)
AR = AR (Common)
ER = FR (R is mid-point of EF)
∴ ∆AER = ∆AFR (SSS axiom)
∴ area(∆AER) = area (∆AFR)
Question 8. In the given figure, X and Y are mid-points of the sides AC and AB respectively of ∆ABC. QP || BC and CYQ and BXP are straight lines. Prove that area of ∆ABP = area of ∆ACQ.
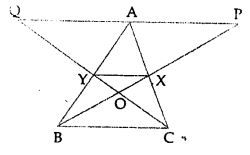
Answer : In the given figure,
X and Y are the mid-points of the sides AC and AB respectively of ∆ABC
QP || BC
CYQ and BXP are straight lines
To prove : area(∆ABP) = area(∆ACQ)
Proof:
v X and Y are the mid-points of sides AC and AB respectively
∴ YX || BC
But QP || BC ∴ QP || BC || YX
In ∆BAP, Y is mid of AB and YX || QP
∴ X is mid-point of BP
∴YX = 1/2 AP …(i)
Similarly we can prove in ∆AQC
YX = 1/2 QA …(ii)
From (i) and (ii),
QA = AP
Now ∆ABP and ∆ACQ are on the equal base and between the same parallel lines
area(∆ABP) = area(∆ACQ)
— : End of ML Aggarwal Theorems on Area Chapter Test Class 9 ICSE Maths Solutions :–
Return to :- ML Aggarawal Maths Solutions for ICSE Class-9
Thanks
Please Share with Your Friends