ML Aggarwal Triangles Chapter Test for ICSE Class 9 Maths Solutions Ch-10

ML Aggarwal Triangles Chapter Test for ICSE Class 9 Maths Solutions Ch-10. Step by Step Answer of Ch-Test Questions of Triangles for ML Aggarwal ICSE Class 9th Mathematics. Visit official website CISCE for detail information about ICSE Board Class-9.

ML Aggarwal Triangles Chapter Test for ICSE Class 9 Maths Solutions Ch-10

Board	ICSE
Subject	Maths
Class	9th
Chapter-10	Triangles
Topics	Solution of Ch-Test Questions
Academic Session	2024-2025

Solution of Ch-Test Questions

ML Aggarwal Triangles for ICSE Class 9 Maths Solutions Ch-10

Question 1. In triangles ABC and DEF, ∠A = ∠D, ∠B = ∠E and AB = EF. Will the two triangles be congruent? Give reasons for your answer.

Answer : In ∆ABC and ∆DEF

∠A = ∠D

∠B = ∠E

AB = EF

In ∆ABC, two angles and included side is

Given but in ∆DEF, corresponding angles are

Equal but side is not included of there angle.

Triangles cannot be congruent.

Question 2.  In the adjoining  figure, ABCD is a square. P, Q and R are points on the sides AB, BC and CD respectively such that AP= BQ = CR and ∠PQR = 90°. Prove that

(a) ∆PBQ ≅ ∆QCR
(b) PQ = QR
(c) ∠PRQ = 45°

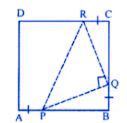
Answer : From the figure, ABCD is a square

P,Q and R are the Points on the sides AB,

BC and CD respectively such that

AP = BQ = CR, ∠PQR = 90^o

To prove: (a) ∆PBQ = ∆QCR

(b) PQ = QR

(c) ∠PQR = 45^o

Proof:

AB = BC = CD (Sides of Square)

And AP = BQ = CR (Given)

Subtracting, we get

AB – AP = BC – BQ = CD – CR (PB = QC = RD)

Now in ∆PBQ and ∠QCR

PB = QC (Proved)

BQ = CR (Given)

∠B = ∠C (Each 90^o)

∆PBQ ≅ ∆QCR

PQ = QR

But ∠PQR = 90^o

∠RPQ = ∠PQR (Angles opposite to equal angles)

But,

∠RPQ + ∠PRQ = 90^o

⇒ ∠RPQ = ∠PQR = 90^o

⇒ ∠RPQ = ∠PRQ = 90^o/2 = 45^o

Question 3. In the given figure, OA ⊥ OD, OC X OB, OD = OA and OB = OC. Prove that AB = CD.

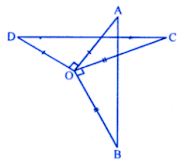
Answer : From the figure OA ⊥ OD, OC ⊥ OB.

∠AOD = ∠COB (each 90^o)

Adding ∠AOC

∠AOD + ∠AOC = ∠AOC + ∠COB

⇒ ∠COD = ∠AOB

Now, in ∆AOB and ∆DOC

OA = OD (Given)

OB = OC (Given)

∠AOB = ∠COD (Proved)

∆AOB ≅ ∆DOC

AB = CD

Question 4. In the given figure, PQ || BA and RS CA. If BP = RC, prove that:

(i) ∆BSR ≅ ∆PQC
(ii) BS = PQ
(iii) RS = CQ.

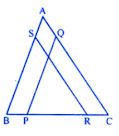
Answer :

PQ ∥ BA, RS ∥ CA

BP = RC

To prove :

(i) ∆BSR ≅ ∆PQC

(ii) RS = CQ

Proof:

BP = RC

⇒ BC – RC = BC – BP

⇒ BR = PC

Now, in ∆BSR and ∆PQC

∠B = ∠P (Corresponding angles)

∠R = ∠C (Corresponding angles)

BR = PC (Proved)

∆BSR ≅ ∆PQC

BS = PQ

RS = CQ

Question 5. In the given figure, AB = AC, D is a point in the interior of ∆ABC such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of ∆ABC.

 

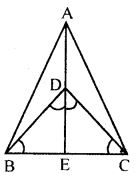
Answer :  Since AB = AC
∠ABC = ∠ACB
But ∠DBC = ∠DBC
⇒ ∠ABD = ∠ACD
Now in ΔABD and ΔADC
AB = AC
AD = AD
∠ABD = ∠ACD
Therefore, ΔABD ≅ ΔADC  …(SSA criteria)
Hence, ∠BAD = ∠CAD
Thus, AD bisects ∠BAC.

Question 6. In the adjoining figure, AB || DC. CE and DE bisects ∠BCD and ∠ADC respectively. Prove that AB = AD + BC.

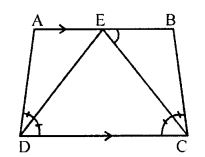
Answer : DE Bisect ∠D

∠EDA = ∠EDC = ∠D/2

AB ║ CD  & DE is line cutting these parallel lines

∠DEA  = ∠EDC  = ∠D/2

in Δ ADE

∠EDA  & ∠DEA = ∠D/2

Hence AD = AE

Similarly

in Δ BCE

∠ECB  = ∠CEB = ∠C/2

BE = BC

AB = AE + BE = AD + BC

AB = AD + BC

Question 7. In ∆ABC, D is a point on BC such that AD is the bisector of ∠BAC. CE is drawn parallel to DA to meet BD produced at E. Prove that ∆CAE is isosceles.

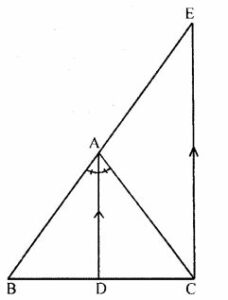
Answer : 

∠BAC  + ∠EAC = 180° ( Straight line)

in ΔACE

∠ACE  + ∠AEC + ∠EAC = 180°  ( sum of angles of Triangle)

Equating both

∠BAC  + ∠EAC = ∠ACE  + ∠AEC + ∠EAC

∠BAC  = ∠ACE  + ∠AEC    Eq 1

∠BAD = (1/2) ∠BAC

∠BAD = ∠AEC  ( AD ║ CE)

∠AEC = (1/2) ∠BAC

putting this in eq 1

∠BAC  = ∠ACE  + (1/2) ∠BAC

∠ACE = (1/2) ∠BAC

∠AEC = ∠ACE = (1/2) ∠BAC

AC = AE

Hence Δ CAE is an isosceles triangle

Question 8. In the figure (ii) given below, ABC is a right angled triangle at B, ADEC and BCFG are squares. Prove that AF = BE.

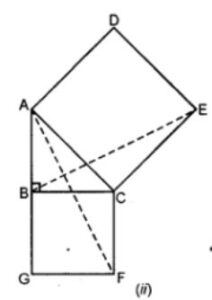
Answer : To prove : AE = BE

angle ACE = angle BCF

adding angle ACB both side

angle ACE +angle ACB = angle BCF + angle ACB
angle BCE = angle ACF

in ∆ BCE and ∆ACF

BC = CF ( square sides)

CE = AF ( square sides)

angle BCE = angle ACF

∆ BCD and ∆ ACF are congruent triangle

BE= AF

Hence Proved

Question 9. In the given figure, BD = AD = AC. If ∠ABD = 36°, find the value of x .

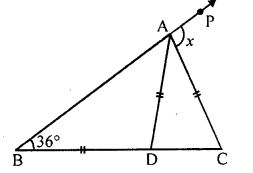
Answer :

Since x is an exterior angle

So we can say,

x = ∠ABD + ∠ ACD

AC = AD = AC

AB = AC

∠ABD = ∠ACD ( 36° = 36°)

x = 36° + 36°

x = 72°

Hence, the value of x is 72° .

Question 10 In the adjoining figure, TR = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that RB = SA.

Answer : Given: In the figure , RST is a triangle

RT = TS         ……..(1)

∠1 = 2∠2        ……..(2)

And∠4 = √2 …………….(3)

And given to prove ΔRBT≅ ΔSAT

Let the point of intersection of RB and SA be denoted by O Since RB and SA intersect at O.

∴∠AOR = ∠BOS          [Vertically opposite angles]

⇒∠1 = ∠4

⇒ 2∠2 = 2∠3                 [From (2) and (3)

∠2 = ∠3                  ……..(4)

Now we have RT = TS  ∠∠TRS

∴ΔTRS is an isosceles triangle

∴∠TRS = ∠TSR            ……..(5)          [Angles opposite to equal sides are equal]   

But we have

 ∠TRS = ∠TRB + ∠2        ………(6)

And ∠TSR = ∠TSA + ∠3     ……….(7)

Putting (6) and (7) in (5) we get

∠TRB +∠2 = ∠TSA + ∠B 

⇒∠ TRB =∠TSA       [∵  From  (4)]

Now considerΔRBT and ΔSAT  

RT = ST             …. [From (1)] 

∠TRB = ∠TSA     ….    [From (4)] 

∠RTB =∠ STA [Common angle] 

From ASA criterion of congruence, we have ΔRBT ≅ΔSAT  

Question 11 .

(a) In the figure (1) given below, find the value of x.
(b) In the figure (2) given below, AB = AC and DE || BC. Calculate

(i)x
(ii) y
(iii) ∠BAC

(c) In the figure (1) given below, calculate the size of each lettered angle.

Answer: Update soon

Question 12.

(a) In the figure (1) given below, AD = BD = DC and ∠ACD = 35°. Show that

(i) AC > DC (ii) AB > AD.

(b) In the figure (2) given below, prove that

(i) x + y = 90° (ii) z = 90° (iii) AB = BC

Answer: Update soon

Question 13. In the adjoining  figure, ABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that

(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.

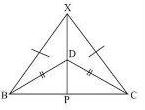
Answer : (i) In △ABD and △ACD,

AB=AC         ….(since △ABC is isosceles)

AD=AD        ….(common side)

BD=DC        ….(since △BDC is isosceles)

ΔABD≅ΔACD     …..SSS test of congruence,

∴∠BAD=∠CAD i.e. ∠BAP=∠PAC          …..[c.a.c.t]……(i)

(ii) In △ABP and △ACP,

AB=AC          …(since △ABC is isosceles)

AP=AP         …(common side)

∠BAP=∠PAC      ….from (i)

△ABP≅△ACP    …. SAS test of congruence

∴BP=PC      …[c.s.c.t]…..(ii)

∠APB=∠APC     ….c.a.c.t.

(iii) Since △ABD≅△ACD

∠BAD=∠CAD     ….from (i)

So, AD bisects ∠A

i.e. AP bisects ∠A…..(iii)

In △BDP and △CDP,

DP=DP     …common side

BP=PC     …from (ii)

BD=CD    …(since △BDC is isosceles)

△BDP≅△CDP    ….SSS test of congruence

∴∠BDP = ∠CDP    ….c.a.c.t.

∴ DP bsects ∠D

So, AP bisects ∠D        ….(iv)

From (iii) and (iv),

AP bisects ∠A as well as ∠D.

(iv) We know that

∠APB+∠APC=180                                  ….(angles in linear pair)

Also, ∠APB=∠APC       …from (ii)

∴∠APB=∠APC =  =90°

BP = PC and ∠APB = ∠APC = 90°

Hence, AP is perpendicular bisector of BC.

Question 14.  In the given figure, AP ⊥ l and PR > PQ. Show that AR > AQ.

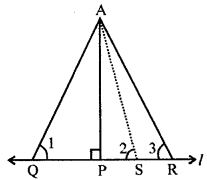
Answer : Given: PR > PQ

Apply Pythagoras theorem in triangle APQ,

AP² = AQ² – PQ²           … (1)

Apply Pythagoras theorem in triangle APR,

AP² = AR² – PR²           … (2)

From equation (1) and (2),

AR² – PR² = AQ² – PQ²

Given PR > PQ, So,

AR² – PQ² > AQ² – PQ²

AR²  >  AQ²

AR > AQ

Hence Proved.

Question 15. If O is any point in the interior of a triangle ABC, show that

OA + OB + OC > 1/2 (AB + BC + CA).

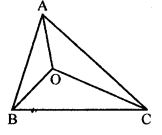
Answer : According to triangle inequality, sum of any two sides is greater than the third side. Therefore,

OA+OB > AB ……(1)

OB+OC > BC ……(2)

OC+OA > AC ……(3)

Adding (1), (2) and (3), we get

2(OA+OB+OC) > (AB+BC+AC)

Dividing both sides by 2, we get

(OA+OB+OC) > 1/2(AB+BC+AC).