ML Aggarwal Trigonometric Identities Chapter Test Solutions ICSE Class-10 Maths Ch-18. We Provide Step by Step Answer of Chapter Test Trigonometric Identities Questions for ICSE Class-10 APC Understanding Mathematics. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Trigonometric Identities Chapter Test Solutions ICSE Class-10 Maths Ch-18
| Board | ICSE |
| Subject | Maths |
| Class | 10th |
| Chapter-18 | Trigonometric Identities |
| Writer / Book | Understanding |
| Topics | Solutions of Chapter Test |
| Academic Session | 2024-2025 |
ML Aggarwal Trigonometric Identities Chapter Test Solutions
ICSE Class-10 Maths Ch-18
Question 1.
(i) If θ is an acute angle and cosec θ = √5 find the value of cot θ – cos θ.
(ii) If θ is an acute angle and tan θ = 8/15, find the value of sec θ + cosec θ.
Answer :
(i) θ is an acute angle.
cosec θ = √5
sin θ = 1/√5
And, cos θ = √(1 – sin2 θ)
cos θ = √(1 – (1/√5)2)
= √(1 – (1/5))
= √(4/5)
cos θ = 2/√5
Now, cot θ – cos θ = (cos θ/sin θ) – cos θ
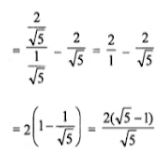
(ii) Given, θ is an acute angle and tan θ = 8/15
In fig. we have
tan θ = BC/AB = 8/15
So, BC = 8 and AB = 15
By Pythagoras theorem, we have
AC = √(AB2 + BC2) = √(52 + 82) = √(25 + 64) = √289
⇒ AC = 17
Now,
sec θ = AC/AB = 17/15
cosec θ = AC/BC = 17/8
So,
sec θ + cosec θ = 17/15 + 17/8
= (136 + 255)/ 120
= 391/120
= 3.31/120
Question 2. Evaluate the following:
(i) 2 × (cos2 20° cos2 70°)/(sin2 25° + sin2 65°) – tan 45° + tan 13° tan 23° tan 30° tan 67° tan 77°
(ii) (sin222° + sin268°)/(cos222° + cos268°) + sin263° + cos63° sin27°
Answer :
(i) 2 × (cos2 20° cos2 70°)/(sin2 25° + sin2 65°) – tan 45° + tan 13° tan 23° tan 30° tan 67° tan 77°

(ii) (sin222° + sin268°)/(cos222° + cos268°) + sin263° + cos63° sin27°
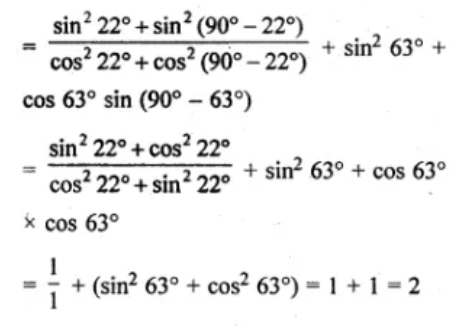
Question 3. If 4/3 (sec2 59° – cot2 31°) – 2/2 sin 90° + 3tan2 56° tan2 34° = x/2, then find the value of x.
Answer :
Given:
4/3 (sec2 59° – cot2 31°) – 2/2 sin 90° + 3tan2 56° tan2 34° = x/2
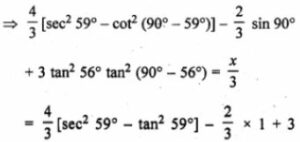
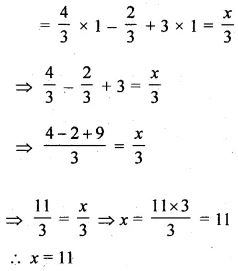
ML Aggarwal Trigonometric Identities Chapter Test Solutions
ICSE Class-10 Maths Ch-11
Page-461
Prove the following (4 to 11) identities, where the angles involved are acute angles for which the trigonometric ratios are defined:
Question 4.
(i) cosA/(1-sinA)+cosA/(1+sinA)=2secA
(ii) cosA/(cosecA+1)+ cosA/(cosecA-1)=2tanA
Answer :
(i) cosA/(1-sinA)+cosA/(1+sinA)=2secA
L.H.S = cosA/(1-sinA)+cosA/(1+sinA)
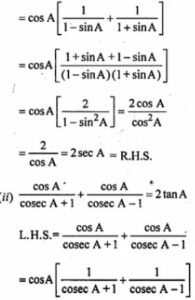

Question 5.
(i) sin2 θ + cos4 θ = cos2 θ + sin4 θ
(ii) cot θ/(cosec θ+1)+(cosec θ+1)/cot θ=2secθ
Answer :
(i) L.H.S. = sin2 θ + cos4 θ = cos2 θ + sin4 θ
L.H.S. = sin2 θ + cos4 θ
= (1 – cos2 θ) + cos4 θ
= cos4 θ – cos2 θ + 1
= cos2 θ (cos2 θ – 1) + 1
= cos2 θ (- sin2 θ) + 1
= 1 – sin2 θ cos2 θ
Now,
R.H.S. = cos2 θ + sin4 θ
= (1 – sin2 θ) + sin4 θ
= sin4 θ – sin2 θ + 1
= sin2 θ (sin2 θ – 1) + 1
= sin2 θ (-cos2 θ) + 1
= 1 – sin2 θ cos2 θ
Hence, L.H.S. = R.H.S.
(ii)
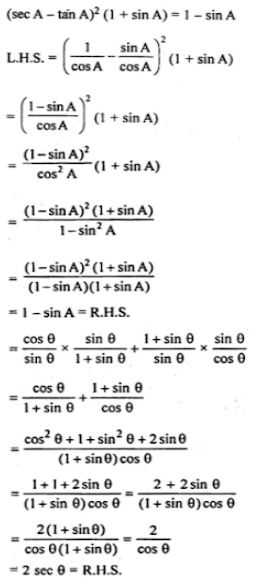
Question 6.
(i) sec4 A (1 – sin4 A) – 2 tan2 A = 1
(ii) 1/(sinA+cosA+1)+1/(sinA+cosA-1) = secA+cosecA
Answer :
(i) sec4 A (1 – sin4 A) – 2 tan2 A = 1
L.H.S = sec4 A (1 – sin4 A) – 2 tan2 A
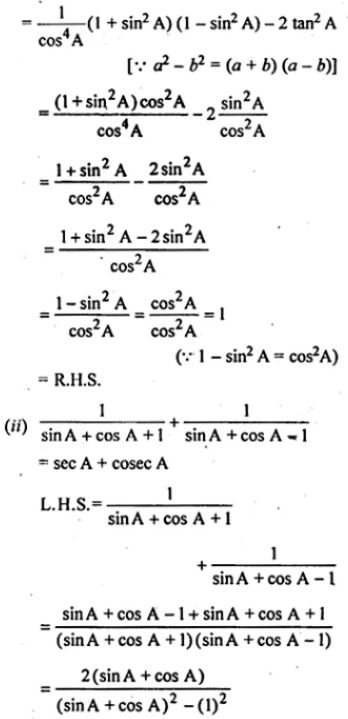

Question 7.
(i) (sin³θ+cos³θ)/sinθcosθ=1
(ii) (sec A – tan A)2 (1 + sin A) = 1 – sin A.
Answer :
(i) (sin³θ+cos³θ)/sinθcosθ=1
L.H.S = (sin³θ+cos³θ)/sinθcosθ
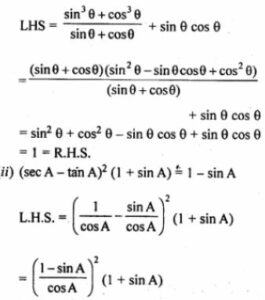
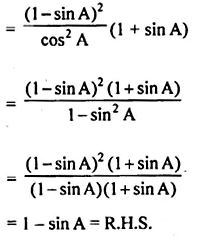
Question 8.
(i) cosA/(1-tanA)-sin²A/(cosA-sinA) = sinA+cosA
(ii) (sec A – cosec A) (1 + tan A + cot A) = tan A sec A – cot A cosec A
(iii) tan²θ/(tan²θ-1)-cosec²θ/(sec²θ-cosec²θ) = 1/(sin²θ-cos²θ)
Answer :
(i) cosA/(1-tanA)-sin²A/(cosA-sinA) = sinA+cosA
L.H.S = cosA/(1-tanA)-sin²A/(cosA-sinA)
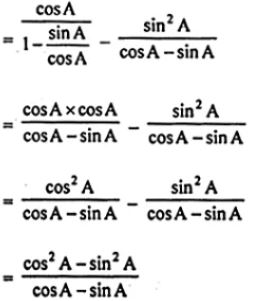


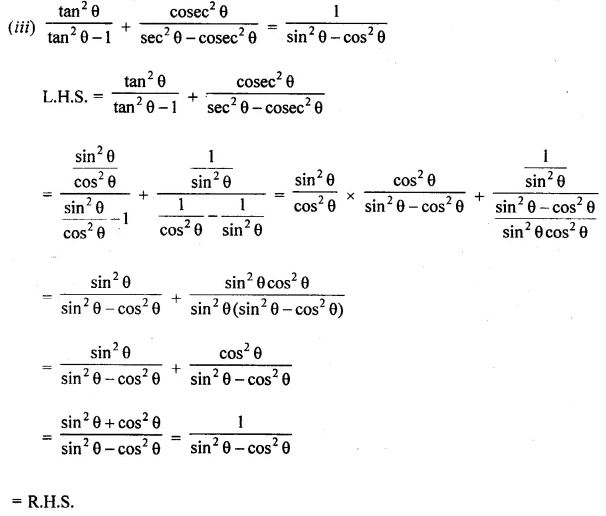
Question 9.
![]()
Answer 9
![]()
L.H.S
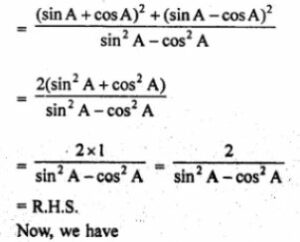
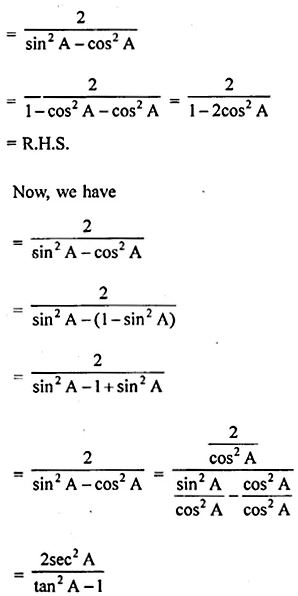
Question 10. 2 (sin6 θ + cos6 θ) – 3 (sin4 θ + cos4 θ) + 1 = θ
Answer :
2 (sin6 θ + cos6 θ) – 3 (sin4 θ + cos4 θ) + 1 = θ
L.H.S = 2 (sin6 θ + cos6 θ) – 3 (sin4 θ + cos4 θ) + 1
= 2 [(sin2 θ)3 + (cos2 θ)3] – 3 (sin4 θ + cos4 θ) + 1
= 2 [(sin2 θ + cos2 θ) (sin4 θ + cos4 θ – sin2 θ cos2 θ)] – 3 (sin4 θ + cos4 θ) + 1
= 2 (sin4 θ + cos4 θ – sin2 θ cos2 θ) – 3 (sin4 θ + cos4 θ) + 1
= 2 sin4 θ + 2 cos4 θ – 2 sin2 θ cos2 θ – 3 sin4 θ – 3 cos4 θ + 1
= 1 – sin4 θ – cos4 θ – 2 sin2 θ cos2 θ
= 1 – (sin2 θ + cos2 θ)2 = 1 – 1 = 0
= R. H. S
Question 11. If cot θ + cos θ = m, cot θ – cos θ = n, then prove that (m2 – n2)2 = 16 mn.
Answer :
cot θ + cos θ = m…..(i)
cot θ – cos θ = n……(ii)
Adding (i)&(ii) we get

Question 12. When 0° < θ < 90°, solve the following equations:
(i) 2 cos2 θ + sin θ – 2 = 0
(ii) 3 cos θ = 2 sin2 θ
(iii) sec2 θ – 2 tan θ = 0
(iv) tan2 θ = 3 (sec θ – 1).
Answer :
0° < θ < 90°
(i) 2 cos2 θ + sin θ – 2 = 0
⇒ 2 (1 – sin2 θ) + sin θ – 2 = 0
⇒ 2 – 2 sin2 θ + sin θ – 2 = 0
⇒ -2 sin2 θ + sin θ = 0
⇒ sin θ (1 – 2 sin θ) = 0
So, either sin θ = 0 or 1 – 2 sin θ = 0
If sin θ = 0
⇒ θ = 0o
And, if 1 – 2 sin θ = 0
sin θ = ½
⇒ θ = 30o
Thus, θ = 0o or 30o
(ii) 3 cos θ = 2 sin2 θ
⇒ 3 cos θ = 2 (1 – cos2 θ)
⇒ 3 cos θ = 2 – 2 cos2 θ
⇒ 2 cos2 θ + 3 cos θ – 2 = 0
⇒ 2 cos2 θ + 4 cos θ – cos θ – 2 = 0
⇒ 2 cos θ (cos θ + 2) – 1(cos θ + 2) = 0
⇒ (2 cos θ – 1) (cos θ + 2) = 0
So, either 2 cos θ – 1 = 0 or cos θ + 2 = 0
If 2 cos θ – 1 = 0
cos θ = ½
⇒ θ = 60o
And, for cos θ + 2 = 0
⇒ cos θ = -2 which is not possible being out of range.
Thus, θ = 60o
(iii) sec2 θ – 2 tan θ = 0
⇒ (1 + tan2 θ) – 2 tan θ = 0
⇒ tan2 θ – 2 tan θ + 1 = 0
⇒ (tan θ – 1)2 = 0
⇒ tan θ – 1 = 0
⇒ tan θ = 1
Thus, θ = 45o
(iv) tan2 θ = 3 (sec θ – 1)
⇒ (sec2 θ – 1) = 3 sec θ – 3
⇒ sec2 θ – 1 – 3 sec θ + 3 = 0
⇒ sec2 θ – 3 sec θ + 2 = 0
⇒ sec2 θ – 2 sec θ – sec θ + 2 = 0
⇒ sec θ (sec θ – 2) – 1 (sec θ = 2) = 0
⇒ (sec θ – 1) (sec θ – 2) = 0
So, either sec θ – 1 = 0 or sec θ – 2 = 0
If sec θ – 1 = 0
sec θ = 1
⇒ θ = 0o
And, if sec θ – 2 = 0
sec θ = 2
⇒ θ = 60o
Thus, θ = 0o or 60o
— : End of ML Aggarwal Trigonometric Identities Chapter Test Solutions ICSE Class-10 Maths Ch-18 : –
Return to :- ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends