ML Aggarwal Trigonometrical Ratios Chapter Test Class 9 ICSE Maths Solutions Ch-17. Step by Step Solutions of Ch-Test Questions on Trigonometrical Ratios of ML Aggarwal for ICSE Class 9th Mathematics. Visit official website CISCE for detail information about ICSE Board Class-9.
ML Aggarwal Trigonometrical Ratios Chapter Test Class 9 ICSE Maths Solutions
| Board | ICSE |
| Subject | Maths |
| Class | 9th |
| Chapter-17 | Trigonometrical Ratios |
| Topics | Solution of Ch-Test Questions |
| Academic Session | 2024-2025 |
Solution of Ch-Test Questions on Trigonometrical Ratios
Question 1.
(a)From the figure (i0) given below, calculate all the six t-ratios for both acute………
(b)From the figure (ii) given below, find the values of x and y in terms of t-ratios
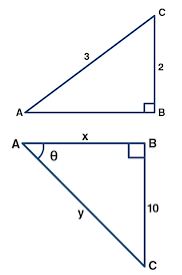
Answer:
(a) From right angled triangle ABC,
AC2 = AB2 + BC2
⇒ AB2 = AC2 – BC2
⇒ AB2 = (3)2 – (2)2
⇒ AB2 = 9 – 4
⇒ AB2 = 5
⇒ AB = √5
(i) sin A = perpendicular/ hypotenuse
= BC/AC
= 2/3
(ii) cos A = base/ hypotenuse
= AB/AC
= √5/3
(iii) tan A = perpendicular/ base
= BC/AB
= 2/ √5
(iv) cot A = base/perpendicular
= AB/ BC
= √5/2
(v) sec A = hypotenuse/ base
= AC/AB
= 3/ √5
(vi) cosec A = hypotenuse/perpendicular
= AC/BC
= 3/2
(b) From right angled triangle ABC,
∠BAC = θ
cotθ = base/ perpendicular
= AB/ BC
= x/ 10
x = 10 cotθ
Also,
cosecθ = hypotenuse/ perpendicular
= AC/ BC
= y/ 10
y = 10 cosec θ
Hence, x = 10 cot θ and y = 10 cosec θ.
Question 2.
(a) From the figure (1) given below, find the values of:
(i) sin ∠ABC
(ii) tan x – cos x + 3 sin x.
(b) From the figure (2) given below, find the values of:
(i) 5 sin x
(ii) 7 tan x
(iii) 5 cos x – 17 sin y – tan x.
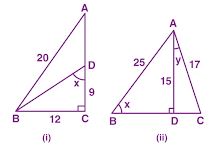
Answer :
(a) BC = 12, CD = 9 and BC = 20
In right angled ∆ABC,
AB2 = AC2 + BC2
AC2 = AB2 – BC2
AC2 = (20)2 – (12)2
AC2 = 400 – 144 = 256
So we get
AC2 = (16)2
⇒ AC = 16
In right angled ∆BCD
BD2 = BC2 + CD2
BD2 = 122 + 92
BD2 = 144 + 81 = 225
BD2 = (15)2
⇒ BD = 15
(i) In right angled ∆BCD
sin ∠ABC = perpendicular/hypotenuse
sin ∠ABC = AC/AB = 16/20 = 4/5
(ii) In right angled ∆BCD
tan x = perpendicular/base
tan x = BC/CD = 12/9 = 4/3
In right angled ∆BCD
cos x = base/hypotenuse
cos x = CD/BD = 9/15 = 3/5
In right angled ∆BCD
sin x = perpendicular/hypotenuse
sin x = BC/BD = 12/15 = 4/5
⇒ tan x – cos x + 3 sin x = 4/3 – 3/5 + (3× 4/5)
= 4/3 – 3/5 + 12/5
Taking LCM
= [(4×5) – (3×3) + (12×3)]/15
= (20 – 9 + 36)/15
= (56 – 9)/15
= 27/15
= 3 (2/15)
Hence, tan x – cos x + 3 sin x = 3 2/15.
(b) AC = 17, AB = 25, AD = 15
In right angled ∆ACD
AC2 = AD2 + CD2
(17)2 = (15)2 + (CD)2
CD2 = (17)2 – (15)2
⇒ CD2 = 289 – 225 = 64
CD2 = 82
⇒ CD = 8
In right angled ∆ABD
AB2 = AD2 + BD2
(25)2 = (15)2 + BD2
BD2 = (25)2 – (15)2
⇒ BD2 = 625 – 225 = 400
So we get
BD2 = (20)2
⇒ BD = 20
(i) In right angled ∆ABD
5 sin x = 5 (perpendicular/hypotenuse)
= 5 (AD/AB)
= 5 × 15/25
= 15/5
= 3
(ii) In right angled ∆ABD
7 tan x = 7 (perpendicular/base)
= 7 (AD/AB)
= 7× 15/20
= 7× ¾
= 21/4
= 5 ¼
(iii) In right angled ∆ABD
cos x = base/hypotenuse
cos x = BD/AB = 20/25 = 4/5
In right angled ∆ACD
sin y = perpendicular/hypotenuse
sin y = CD/AC = 8/17
In right angled ∆ABD
tan x = perpendicular/base
tan x = AD/BD = 15/20 = ¾
5 cosx – 17 siny – tanx = (5× 4/5) – (17× 8/17) – ¾
It can be written as
= 4/1 – 8/1 – ¾
Taking LCM
= (16 – 32 – 3)/4
= (16 – 35)/4
= –19/4
= –4 ¾
Hence, 5 cos x – 17 sin y – tan x = – 4 ¾.
Question 3. If q cosθ = p, find tanθ – cotθ in terms of p and q.
Answer :
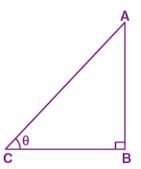
Consider ABC as a triangle right angled at B and ∠ACB = θ
q cos θ = p
cos θ = BC/AC = p/q
Take BC = px then AC = qx
In right angled ∆ABC
AC2 = AB2 + BC2
AB2 = AC2 – BC2
AB2 = (qx)2 – (px)2
⇒ AB2 = q2x2 – p2x2
AB2 = (q2 – p2)x2
AB = √(q2 – p2) x2
⇒ AB = (√q2 – p2)x
In right angled ∆ABC
tan θ = perpendicular/base
tan θ = AB/BC = [(√q2 – p2)x]/px
⇒ tan θ = (√q2 – p2)/p
In right angled ∆ABC
cot θ = base/perpendicular
cot θ = BC/AB = px/[(√q2 – p2)x]
⇒ cot [(√q2 – p2)x] = p/(√q2 – p2)
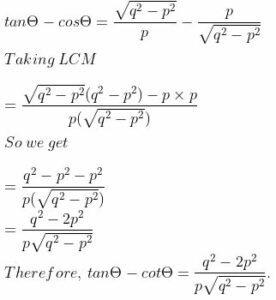
Question 4. Given 4 sin θ = 3 cos θ, find the values of:
(i) sin θ
(ii) cos θ
(iii) cot2 θ – cosec2 θ.
Answer :
4 sin θ = 3 cos θ
⇒ sin θ/cos θ = ¾
⇒ tan θ = ¾
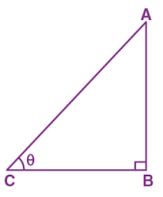
Consider ∆ABC right angled at B and ∠ACB = θ
tan θ = perpendicular/base
¾ = AB/BC
⇒ AB/BC = ¾
Take AB = 3x then BC = 4x
In right angled ∆ABC
AC2 = AB2 + BC2
AC2 = (3x)2 + (4x)2
AC2 = 9x2 + 16x2 = 25x2
AC2 = (5x)2
⇒ AC = 5x
(i) In right angled ∆ABC
sin θ = perpendicular/hypotenuse
sin θ = AB/AC = 3x/5x = 3/5
(ii) In right angled ∆ABC
cos θ = base/hypotenuse
cos θ = BC/AC = 4x/5x = 4/5
(iii) In right angled ∆ABC
cot θ = base/perpendicular
cot θ = BC/AB = 4x/3x = 4/3
In right angled ∆ABC
cosec θ = hypotenuse/perpendicular
cosec θ = AC/AB = 5x/3x = 5/3
cot2 θ – cosec2 θ = (4/3)2 – (5/3)2
= 16/9 – 25/9
= (16 – 25)/9
= -9/9
= -1
Hence, cot2 θ – cosec2 θ = -1.
Question 5. If 2 cos 0 = 3, prove that 3 sin 0 – 4 sin3 0 = 1.
Answer :
2 cos θ = √3
⇒ cos θ = √3/2
sin2 θ = 1 – cos2 θ
= 1 – (√3/2)2
= 1 – ¾
= ¼
sin θ = √ ¼ = ½
LHS = 3 sin θ – 4 sin3 θ
= sinθ (3 – 4sin2 θ)
= ½ [3 – (4 × ¼)]
= ½ (3 – 1)
= ½ × 2
= 1
= RHS
Hence proved.
Question 6. If (sec θ – tan θ)/ (sec θ + tan θ) = ¼, find sin θ.
Answer :
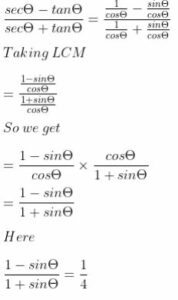
4 – 4 sin θ = 1 + sin θ
4 – 1 = sin θ + 4 sin θ
⇒ 3 = 5 sin θ
⇒ sin θ = 3/5
Question 7. If sin θ + cosec θ = 3 1/3, find the value of sin2 θ + cosec2 θ.
Answer :
sin θ + cosec θ = 3 1/3 = 10/3
By squaring on both sides
(sin θ + cosec θ)2 = (10/3)2
Expanding using formula (a + b)2 = a2 + b2 + 2ab
sin2 θ + cosec2 θ + 2 sin θ cosec θ = 100/9
We know that sin θ = 1/cosec θ
sin2 θ + cosec2 θ + (2 sinθ× 1/sin θ) = 100/9
sin2 θ + cosec2 θ + 2 = 100/9
⇒ sin2 θ + cosec2 θ = 100/9 – 2
Taking LCM
sin2 θ + cosec2 θ = (100 – 18)/9 = 82/9
sin2 θ + cosec2 θ = 9 1/9
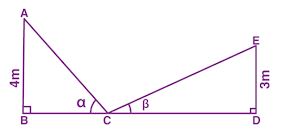
Question 8. In the adjoining figure, AB = 4 m and ED = 3 m.
If sin α = 3/5 and cos β = 12/13, find the length of BD.
Answer :
sin α = AB/AC = 3/5
AB = 3 and AC = 5
AC2 = AB2 + BC2
52 = 32 + BC2
25 = 9 + BC2
⇒ BC2 = 25 – 9 = 16
BC2 = 42
⇒ BC = 4
tan α = AB/BC = 4/5
cos β = CD/CE = 12/13
CD = 12 and CE = 13
CE2 = CD2 + ED2
132 = 122 + ED2
ED2 = 132 – 122
⇒ ED2 = 169 – 144 = 25
ED2 = (5)2
⇒ ED = 5
⇒ tan β = ED/CD = 5/12
tan α = AB/BC = 4/BC
¾ = 4/BC
⇒ BC = (4×4)/3 = 16/3 m
tan β = ED/CD = 3/CD
⇒ 5/12 = 3/CD
CD = (12 × 3)/5 = 36/5 m
Here,
BD = BC + CD
= 16/3 + 36/5
Taking LCM
= (80 + 108)/15
= 188/15 m
= 12 8/15 m
— : End of ML Aggarwal Trigonometrical Ratios Chapter Test Class 9 ICSE Maths Solutions :–
Return to :- ML Aggarawal Maths Solutions for ICSE Class-9
Thanks
Please Share with Your Friends