ML Aggarwal Trigonometrical Ratios of Standards Angles Chapter Test Class 9 ICSE Maths Solutions Ch-18. Step by Step Solutions of Ch-Test questions on Trigonometrical Ratios of of Standards Angles for ML Aggarwal ICSE Class 9th Mathematics. Visit official website CISCE for detail information about ICSE Board Class-9.
ML Aggarwal Trigonometrical Ratios Chapter Test Class 9 ICSE Maths Solutions
| Board | ICSE |
| Subject | Maths |
| Class | 9th |
| Chapter-18 | Trigonometrical Ratios of Standards Angles |
| Topics | Solution of Ch-Test Questions |
| Academic Session | 2024-2025 |
Solution of Ch-Test Questions on Trigonometrical Ratios of Standards Angles
ML Aggarwal Class 9 ICSE Maths Solutions Ch-18
Question 1 Find the values of:
(i) sin2 60° – cos2 45° + 3tan2 30°
(ii)……………..
(iii) sec 30° tan 60° + sin 45° cosec 45° + cos 30° cot 60°
Answer :
(i) sin2 60° – cos2 45° + 3tan2 30°
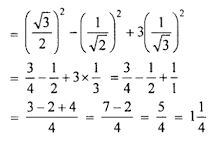
Therefore, sin2 60° – cos2 45° + 3tan2 30° = 1¼

(iii) sec 30° tan 60° + sin 45° cosec 45° + cos 30° cot 60°
![]()
= 2 + 1 + ½ = 3 + ½ = (6 + 1)/2
= 7/2 = 3½
Thus,
sec 30° tan 60° + sin 45° cosec 45° + cos 30° cot 60° = 3½
Question 2. Taking A = 30°, verify that
(i) cos4 A – sin4 A = cos 2A
(ii) 4cos A cos (60° – A) cos (60° + A) = cos 3 A.
Answer :
(i) cos4 A – sin4 A = cos 2A
Let’s take A = 30°
so,
we have
L.H.S.= cos4 A – sin4 A = cos4 30° – sin4 30°
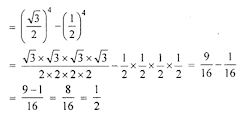
R.H.S. = cos 2A = cos 2(30o) = ½
Therefore, L.H.S. = R.H.S. hence verified.
(ii) 4 cos A cos (60°- A) cos (60° + A) = cos 3 A
Let’s take A = 30°
L.H.S. = 4 cos A cos (60° – A) cos (60° + A)
= 4 cos 30° cos (60° – 30°) cos (60° + 30°)
= 4 cos 30° cos 30° cos 90°
= 4 × (√3/2) × (√3/2) × 0
= 0
R.H.S. = cos 3A
= cos (3 × 30°) = cos 90° = 0
Therefore, L.H.S. = R.H.S.
Hence proofed
Question 3. If A = 45° and B = 30°, verify that sin A/ (cos A + sin A + sin B) = 2/3
Answer :

Hence proofed
Question 4. Taking A = 60° and B = 30°, verify that
(i) sin (A + B)/cos A cos B = tan A + tan B
(ii) sin (A – B)/sin A sin B = cot B – cot A
Answer :
(i) Here, A = 60° and B = 30°

Question 5. If √2 tan 2θ = √6 and θ° < 2θ < 90°, find the value of sin θ + √3 cos θ – 2 tan2 θ.
Answer :
√2 tan 2θ = √6
⇒ tan 2θ = √6/ √2
= √3
= tan 60o
⇒ 2θ = 60o
⇒ θ = 30o
sin θ + √3 cos θ – 2 tan2 θ
= sin 30o + √3 cos 30o – 2 tan2 30o
= ½ + √3 x √3/2 – 2 (1/√3)2
= ½ + 3/2 – 2/3
= 4/2 – 2/3
= (12 – 4)/6
= 8/6
= 4/3
Question 6. If 3θ is an acute angle, solve the following equations for θ:
(i) (cosec 3θ – 2) (cot 2θ – 1) = 0
(ii) (tan θ – 1) (cosec 3θ – 1) = 0
Answer :
(i) (cosec 3θ – 2) (cot 2θ – 1) = 0
cosec 3θ – 2 or cot 2θ – 1 = 0
⇒ cosec 3θ = 2 or cot 2θ = 1
So,
cosec 3θ = cosec 3θ° or cot 2θ =cot 45°
⇒ 3θ = 30° or 2θ = 45°
Thus,
θ = 30° or 45°.
(ii) (tan θ – 1) (cosec 3θ – 1) = 0
tan θ – 1 = 0 or cosec 3θ – 1 = 0
⇒ tan θ = 1 or cosec 3θ = 1
So,
tan θ = tan45° or cosec 3 θ = cosec 90°
⇒ θ = 45° or 3θ = 90° i.e. θ = 30°
Thus,
θ = 45° or 30°.
Question 7. If tan (A + B) = √3 and tan (A – B) = 1 and A, B (B < A) are acute angles, find the values of A and B.
Answer :
tan (A + B) = √3
So, tan (A + B) = tan 60° [Since, tan 60° = √3]
⇒ A + B = 60° …(i)
tan (A – B) = 1
tan (A – B) = tan 45° [tan 45° = 1]
⇒ A – B = 45° …(ii)
From equation (1) and (2), we get
A + B + A – B = 60° + 45°
⇒ 2A = 105o
⇒ A = 52½o
on substituting the value of A in equation (i), we get
52½o + B = 60°
⇒ B = 60° – 52½o = 7½o
Therefore, the value of A = 52½o and B = 7½o
Question 8. Without using trigonometrical tables, evaluate the following:
(i) sin2 28° + sin2 62° – tan2 45°
(ii)…………………………
(iii) cos 18° sin 72° + sin 18° cos 72°
Answer :
(i) sin2 28° + sin2 62° – tan2 45°
= sin2 28° + sin2 (90° – 28°) – tan2 45°
= sin2 28° + cos2 28° – tan2 45°
= 1 – (1)2 (∵ sin2 θ + cos2 θ = 1 and tan 45° = 1)
= 1 – 1
= 0

= (2×1) + 1 + 1
= 2 + 1 + 1
= 4
(iii) cos 18° sin 12° + sin 18° cos 12°
= cos (90° – 12°) sin 72° + sin (90° – 12°) cos 12°
= sin 72°.sin 12° + cos 12° cos 12°
= sin2 12° + cos2 12°
= 1 (∵ sin2 θ + cos2 θ = 1)
(iv) 5 sin 50° sec 40° – 3 cos 59° cosec 31°
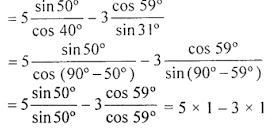
= 5 – 3
= 2
Question 9. Prove that:
……………………..
Answer :
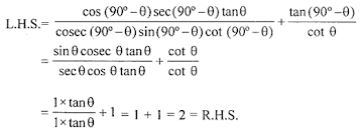
L.H.S. = R.H.S.
Hence proved.
Question 10. When 0° < A < 90°, solve the following equations:
(i) sin 3A = cos 2A
(ii) tan 5A = cot A
Answer :
(i) sin 3A = cos 2A
⇒ sin 3A = sin (90° – 2A)
3A = 90° – 2A
⇒ 3 A + 2A = 90°
⇒ 5A = 90°
∴ A = 90°/5 = 18°
⇒ tan 5A = cot A
⇒ tan 5A = tan (90° – A)
5A = 90°- A
⇒ 5A + A = 90°
⇒ 6A = 90°
∴ A = 90°/6 = 15°
Question 11. Find the value of θ if
(i) sin (θ + 36°) = cos θ, where θ and θ + 36° are acute angles.
(ii) sec 4θ = cosec (θ – 20°), where 4θ and θ – 20° are acute angles.
Answer :
(i) Given, θ and (θ + 36°) are acute angles
sin (θ + 36°) = cos θ = sin (90° – θ) [As, sin (90° – θ) = cos θ]
θ + 36° = 90° – θ
⇒ θ + θ = 90° – 36°
⇒ 2θ = 54°
⇒ θ = 54°/2
∴ θ = 27°
(ii) Given, θ and (θ – 20°) are acute angles
And,
sec 4θ = cosec (θ – 20°)
⇒ cosec (90° – 4θ) = cosec (θ – 20°) [Since, cosec (90° – θ) = sec θ]
On comparing, we get
90° – 4θ = θ – 20°
⇒ 90° + 20° = θ + 4θ
⇒ 5θ = 110°
⇒ θ = 110°/5
∴ θ = 22°
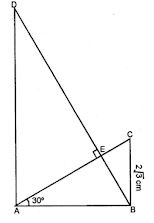
Question 12. In the adjoining figure, ABC is right-angled triangle at B and ABD is right angled triangle at A. If BD ⊥ AC and BC = 2√3cm, find the length of AD.
Answer :
∆ABC and ∆ABD are right angled triangles in which ∠A = 90° and ∠B = 90°
BC = 2√3 cm. AC and BD intersect each other at E at right angle and ∠CAB = 30°.
Now in right ∆ABC, we have
tan θ = BC/AB
⇒ tan 30° = 2√3/ AB
⇒ 1/√3 = 2√3/ AB
⇒ AB = 2√3 × √3 = 2 × 3 = 6 cm.
In ∆ABE, ∠EAB = 30° and ∠EAB = 90°
∠ABE or ∠ABD = 180° – 90° – 30°
= 60°
Now in right ∆ABD, we have
tan 60° = AD/AB
⇒ √3 = AD/6
Thus, AD = 6√3 cm.
— : End of ML Aggarwal Trigonometrical Ratios of Standards Angles Chapter Test Class 9 ICSE Maths Solutions :–
Return to :- ML Aggarawal Maths Solutions for ICSE Class-9
Thanks
Please Share with Your Friends