ML Aggarwal Circle Exe-15 Class 8 ICSE Ch-15 Maths Solutions. We Provide Step by Step Answer of Exe-15 Questions for Circle as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-8.
ML Aggarwal Circle Exe-15 Class 8 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 8th |
| Chapter-15 | Circle |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-15 Questions |
| Edition | 2023-2024 |
Circle Exe-15
ML Aggarwal Class 8 ICSE Maths Solutions
Page-264
Question 1. Draw a circle with centre O and radius 2-5 cm. Draw two radii OA and OB such that ∠ AOB = 60°. Measure the length of the chord AB.
Answer:
- Draw a circle with centre O and radius = 2·5 cm.
- Join OA where A is any point on the circle.
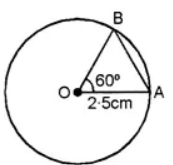
- Draw ∠AOB = 60°.
- Join AB and on measuring we get AB = 2·5 cm.
Question 2. Draw a circle of radius 3·2 cm. Draw a chord AB of this circle such that AB = 5 cm. Shade the minor segment of the circle.
Answer:
- Draw a circle with centre C and radius 3·2 cm.
- Take a point A on the circle.
- With A as centre and radius = 5 cm,
draw an arc to meet the circle at B - Join AB and shade the minor segment.

Question 3. Find the length of the tangent drawn to a circle of radius 3 cm, from a point at a distance 5 cm from the centre.
Answer:
Draw a circle with centre C and radius CT = 3 cm.
Let PT be the tangent drawn from
point P to a circle with centre C.
CP = 5 cm
CT = 3 cm (given radius)

∠CTP = 90°
∵ Radius is ⊥ to tangent
From ∆CPT,
by Pythagoras theorem, we get
CP2 = PT2 + CT2
(5)2 = PT2 + 32
PT2 = 25 – 9 = 16
PT = √16 = 4
Hence, length of tangent = 4 cm
Question 4. In the adjoining figure, PT is a tangent to the circle with centre C. Given CP = 20 cm and PT = 16 cm, find the radius of the circle.

Answer:
We know that, radius is always ⊥ to longest.
i. e., CT ⊥ PT
∴ ∆CPT is right ∠d ∆
Where CP = hypotenuse
In rt. ∆CPT, by Pythagoras theorem,
CP2 = PT2 + CT2
CT2 = CP2 – PT2 = 202 – 162 = 400 – 256 = 144
CT = √144 = 12 cm
Hence, radius of circle = 12 cm
Question 5. In each of the following figure, O is the centre of the circle. Find the size of each lettered angle :
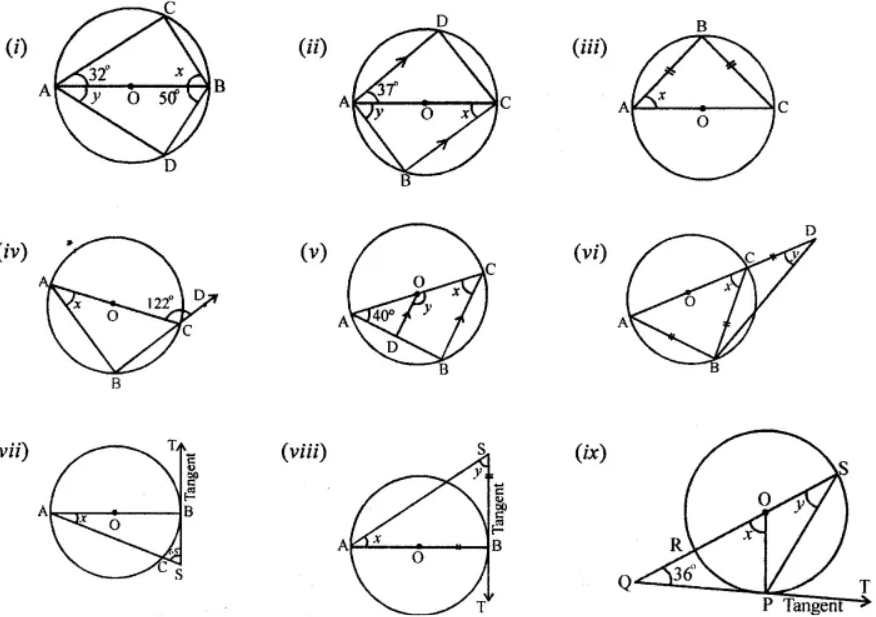
Answer:
(i) In the figure, AB is the diameter
and O is the centre of the circle ∠ CAB = 32°,
∠ ABD = 50° , ∠C = 90° (Angle in the semicircle)
By ∠ sum property of ∆
In ∆ABC, ∠C + ∠CAB + ∠ABC = 180°
⇒ 90° + ∠CAB + x = 180°
⇒ 32° + x = 180° – 90°
⇒ x = 90° – 32°
⇒ x = 58°
Similarly in right ∆ ADB
∠ADB = 90°
By ∠ sum property of ∆
∠ABD + ∠D + ∠BAD = 180°
⇒ 50° + 90° + ∠BAD = 180°
⇒ ∠y + 140° = 180°
⇒ ∠y = 180° – 140° = 40°
⇒ ∠y = 40°
(ii) In the figure,
AC in the diameter of circle with centre O
∠DAC = 37°, AD || BC
∵ AD || BC
∠ACB = ∠DAC (Alternate angles)
∴ x = 37°
In ∆ABC, ∠B = 90° (Angle in a semicircle)
∴ By ∠sum property of ∆
∠x + ∠y + ∠B = 180°
⇒ 37° + ∠y + 90° = 180°
⇒ y = 180° – 127° = 53°
(iii) In the figure,
AC is the diameter of the circle with centre O.
BA = BC
∴ ∠BAC = ∠BCA (∠s of isosceles ∆)
But ∠ABC = 90° (Angle in a semicircle)
In ∆ABC
(By ∠ sum property of ∆)
∠BAC + ∠ABC + ∠BCA = 180°
⇒ ∠BAC + ∠BCA = 180°- 90°
⇒ x + x = 90°
⇒ 2x = 90°
∴ x = 45°
(iv) In the figure,
AC is the diameter of the centre with centre O,
∠ACD = 122°
∵ ∠ACB + ∠ACD = 180° (Linear pair)
⇒ ∠ACB + 122° = 180°
⇒ ∠ACB + 180° – 122° = 58°
In ∆ABC, ∠ABC = 90° (Angle in a semicircle)
∴ By angle sum prop, of ∆
∠ABC + ∠BCA + ∠ACB = 180°
90° + 58° + x = 180°
x = 180°- 148° = 32°
(v) In the figures,
AC is the diameter of the circle with centre O,
OD || CB and ∠CAB = 40°
In ∆ABC,
∠B = 90°, (Angle in a semicircle)
By ∠ sum prop, of ∆
∠BCA + ∠ABC + ∠BAC = 180°
∠BCA + ∠CAB + 90° = 180°
∴ ∠BCA + ∠CAB = 90°
⇒ x + 40° = 90° ⇒ x = 90°- 40°= 50°
∴ x = 50°
∵ OD || CB
so ∴ ∠AOD = ∠BCA (corresponding angles)
∠AOD = x = 50°
But ∠AOD + ∠DOC = 180° (Linear pair)
⇒ 50°+ y = 180° ⇒ y = 180°- 50°= 130°
Hence x = 50° and y = 130°
(vi) In the figure,
AC is the diameter of the circle with centre O
BA = BC = CD
In ∆ABC,
∠ABC = 90° (Angle in a semicircle)
By ∠ sum prop, of ∆
∠BAC + ∠BCA + ∠ABC = 180°
∠BAC + ∠BCA + 90° = 180°
∴ ∠BAC + ∠BCA = 90°
But BA = BC (given)
∴ ∠BAC = ∠BCA = x
∴ x + x = 90°
2x = 90°
∴ x = 45°
In ∆BCD,
BC = CD
∴ ∠CBD = ∠CDB = y
and ext. ∠ACB = Sum of interior opposite angles
∠CBD + ∠CDB
x = y + y = 2y
∴ 2y = 45°
y = 45°/2 = 22.5° or 22(1/2)°
(vii) In the figure,
AB is the diameter of circle with centre O.
ST is the tangent at B
∠ASB = 65°
In ∆ABS
∵ TS is the tangent and OB is the radius
OB ⊥ ST or ∠ABS = 90°
But in ∆ASB
∠BAC + ∠ASB + ∠ABS = 180° (Angles of a triangle)
x + 65° + 90° = 180°
⇒ x° + 155° = 180° ⇒ x = 180° – 155° = 25°
Hence x = 25°
(viii)In the figure,
AB is the diameter of the circle with centre
O. ST is the tangent to the circle at B.
AB = BS
∴ ST is the tangent and OB is the radius
∴ OB ⊥ ST or ∠OBS = 90°
∴ In ∆ABS,
∠BAS + ∠BSA + ∠ABS = 180°
[By ∠ sum property of ∆]
⇒ ∠BAS + ∠BSA + 90° = 180°
∠BAS + ∠BSA = 90° ⇒ x + y = 90°
∵ AB = BS
∴ x = y
hence ∴ x = y = 90°/2 = 45°
(ix) In the figure,
RS is the diameter of the circle with centre O.
SR is produced to Q. QT is tangent to the circle at P
OP is joined.
∠Q = 36°
QPT is tangent and OP is the radius of the circle
∴. OP ⊥ QT
∠OPQ = 90°
∴ Now in ∆OPQ
By ∠ sum prop, of ∆
∠OQP + ∠POQ + ∠OPQ = 180°
∠OQP + ∠POQ + 90° = 180°
∴ ∠OQP + ∠POQ = 90°
⇒ 36° + x = 90° ⇒ x = 90° – 36° = 54°
In ∆OPS, OP = OS (Radii of the circle)
∴ ∠OPS = ∠OSP = y
and Ext. ∠POQ = ∠OPS + ∠OSP
= y + y = 2y
⇒ 2y = x = 54°
Circle Exe-15
ML Aggarwal Class 8 ICSE Maths Solutions
Page-265
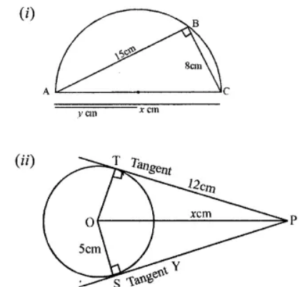
Question 6. In each of the following figures, O is the j centre of the circle. Find the values of x and y.
Answer
(i) O is the centre of the circle
AB = 15 cm, BC = 8cm
∠ABC = 90° (Angles in a semicircle)
By Pythagoras Theorem,
AC2 = AB2 + AC2
= (15)2 + (8)2 = 225 + 64
= 289 = (17)2
∴ AC = 17 cm
∴ x = 17 cm
and ∴ y = 1/2
(∵ AC is the diameter and AO is the radius of the circle)
= 1/2 × 17 = 17/2 cm = 8.5 cm
(ii) O is the centre of the circle.
PT and PS are the tangents to the circle from P.
OS and OT are the radii of the circle
∴ ∠OSP = ∠OTP = 90°
OS = OT = 5 cm, PT = PS = 12 cm
Now in right ∆OPT (By Pythagoras Theorem)
OP2 = OT2 + PT2 = (5)2 + (12)2
= 25 + 144 = 169 = (13)2
∴ OP = 13 cm ⇒ x = 13cm
∵ PS = PT = 12 cm
∴ y = 12 cm
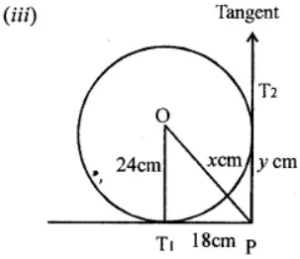
(iii) O is the centre of the circle OT1 is the radius,
From P, PT1 and PT2 are the tangents.
OT1 = 24 cm PT1 = 18cm
∵ OT, is the radius and PT1 is the tangent
∴ OT1 ⊥ PT1
Now in right ∆OPT, (By Pythagoras Theorem)
OP2 = OT12 + PT12 = (24)2 + (18)2
= 576 + 324 = 900 = (30)2
∴ OP = 30
⇒ x = 30 cm
∵ PT1 and PT2 are the tangents from P
∴ PT2 = PT1 = 18 cm
⇒ y = 18 cm
— End of Circle Exe-15 Class 8 ICSE Maths Solutions :–
Return to : – ML Aggarwal Maths Solutions for ICSE Class -8
Thanks


