Circle Theorem Class-9th Concise Selina ICSE Mathematics Solutions Chapter-17 by RK Bansal . We provide step by step Solutions of Exercise / lesson-17 Circle Theorem for ICSE Class-9 Concise Selina Mathematics by R K Bansal.
Our Solutions contain all type Questions with Exe-17 A , Exe-17 B, Exe-17 C and Exe-17 D, to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-9 Mathematics .
Circle Theorem Class-9th Concise Selina ICSE Mathematics Solutions Chapter-17
–: Select Topics :–
Exercise-17 A, Circle Theorem Class-9th Concise Selina ICSE Mathematics Solutions
Question 1
A chord of length 6 cm is drawn in a circle of radius 5 cm. Calculate its distance from the center of the circle.
Answer
Let AB be the chord and O be the centre of the circle.
Let OC be the perpendicular drawn from O to AB.
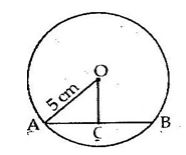
We know, that the perpendicular to a chord, from the centre of a circle, bisects the chord.
AC = CB = 3 cm
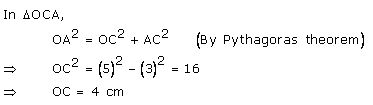
Question 2
A chord of length 8 cm is drawn at a distance of 3 cm from the centre of the circle. Calculate the radius of the circle.
Answer
Let AB be the chord and O be the centre of the circle.
Let OC be the perpendicular drawn from O to AB.

Hence, radius of the circle is 5 cm.
Question 3
The radius ……………………….the chord .
Answer
Question 4
A chord of length 24 cm is at a distance of 5 cm from the centre of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the centre.
Answer
Let AB be the chord of length 24 cm and O be the centre of the circle.
Let OC be the perpendicular drawn from O to AB.
We know, that the perpendicular to a chord, from the centre of a circle, bisects the chord.
AC = CB = 12 cm
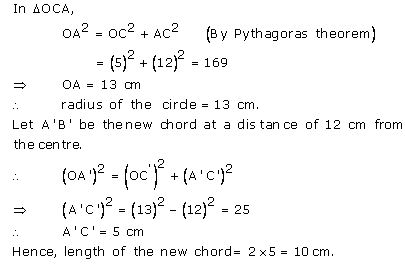
Question 5
In the following figure, AD is a straight line,…….. and O is the centre of both the circles. If OA = 34cm, OB = 20 cm and OP = 16 cm; find the length of AB.
………………
Answer
We know that the perpendicular to a chord, from the centre of a circle, bisects the chord.
AP = PD
By Pythagoras Theorem,
OA2 = OP2 + AP2
=> AP2 = (34)2 – (16)2 = 900
=> AP = 30 cm
AB = AP – BP = 30 – 12 = 18 cm
Question 6
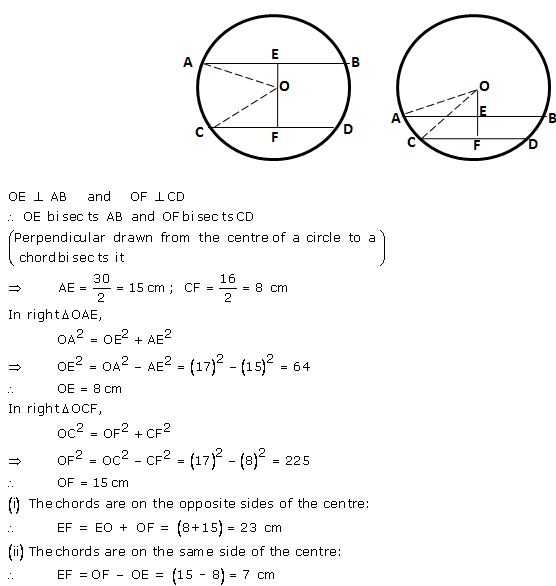
In a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. Find the distance between the chords, if both the chords are:
(i) on the opposite sides of the centre;
(ii) on the same side of the centre.
Answer
Let O be the centre of the circle and AB and CD be the two parallel chords of length 30 cm and 16 cm respectively.
Drop OE and OF perpendicular on AB and CD from the centre O.
Question 7
Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm; find the length of another chord.
Answer
Since the distance between the chords is greater than the radius of the circle (15 cm), so the chords will be on the opposite sides of the centre.

Question 8
A chord CD of a circle whose centre is O, is bisected at P by a diameter AB. Given OA = OB = 15 cm and OP = 9 cm. Calculate the lengths of:
(i) CD ; (ii) AD ; (iii) CB.
Answer
Question 9
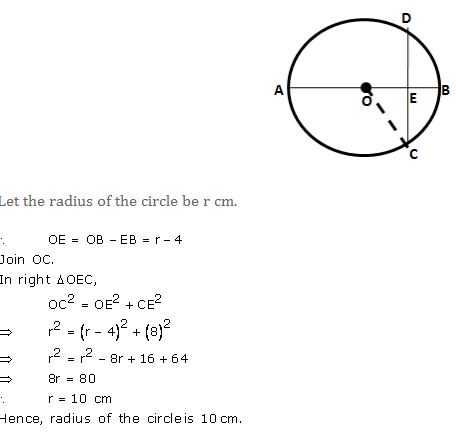
The figure given below shows a circle with centre O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm, find the radius of the circle.
…………..
Answer
Question 10
In the given figure, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm, Find the :
(i) radius of the circle
(ii) length of chord CD
Answer

Exercise-17 B Circle Theorem Class-9th Concise Selina ICSE Mathematics Solutions
Question 1
The figure shows two concentric circles and AD is a chord of larger circle. Prove that: AB = CD.
……………….
Answer
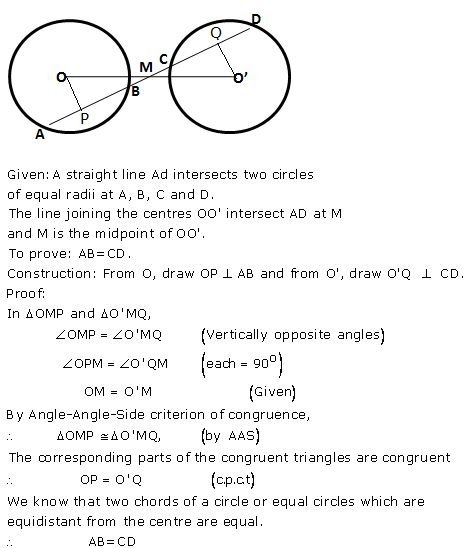
Question 2
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centres O and O’. Prove that the chords AB and CD, which are intercepted by the two circles, are equal.
……………….
Answer
Question 3
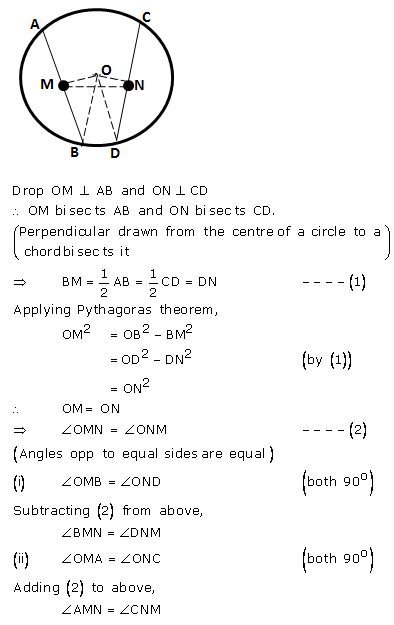
M and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. Prove that:
(i)………………..
(ii)…………..
Answer
Question 4
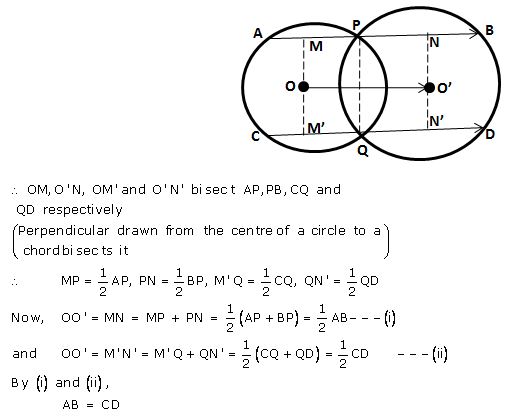
In the following figure; P and Q are the points of intersection of two circles with centres O and O’. If straight lines APB and CQD are parallel to OO’; prove that:
(i)………………..
(ii)…………..
Answer
Drop OM and O’N perpendicular on AB and OM’ and O’N’ perpendicular on CD.
Question 5
Two equal chords AB and CD of a circle with centre O, intersect each other at point P inside the circle. Prove that:
(i) AP = CP ; (ii) BP = DP
………..
Answer
Drop OM and ON perpendicular on AB and CD.
Join OP, OB and OD.

Question 6
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q. Prove that:
(i)………………..
(ii)…………..
Answer
Question 7
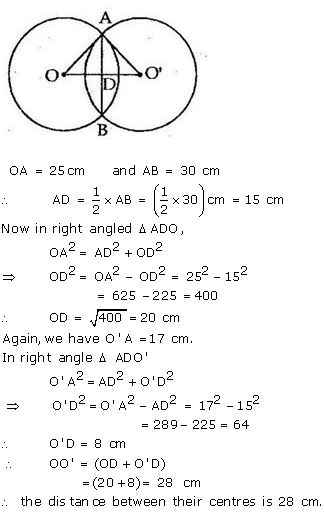
The length of the common chord of two intersecting circles is 30 cm. If the diameters of these two circles be 50 cm and 34 cm, calculate the distance between their centres.
Answer
Question 8
The line joining the midpoints of two chords of a circle passes through its centre. Prove that the chords are parallel.
Answer
Question 9
In the following figure, the line ABCD is perpendicular to PQ; where P and Q are the centres of the circles. Show that:
(i) AB = CD ;
(ii) AC = BD.
………….
Answer
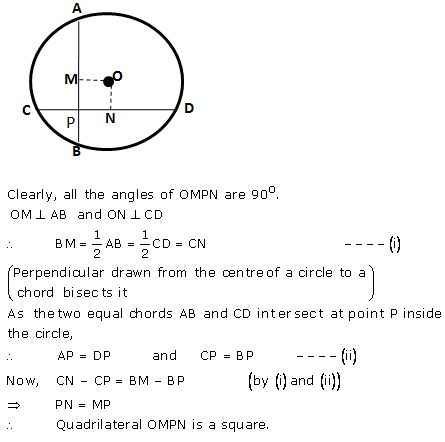
Question 10
AB and CD are two equal chords of a circle with centre O which intersect each other at right angle at point P. If OM AB and ONCD; show that OMPN is a square.
Answer
Exercise-17 C, Circle theorem Class-9th Concise Selina ICSE Mathematics Solutions
Question 1
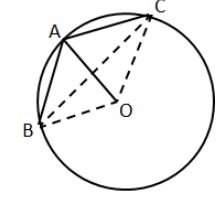
In the given figure, an equilateral triangle ABC is inscribed in a circle with centre O.
Find: (i) ∠BOC (ii) ∠OBC
……………
Answer

In the given figure, ABC is an equilateral triangle.
Hence all the three angles of the triangle will be equal to 60°
i.e. ∠A = ∠B = ∠C = 60°
As the triangle is an equilateral triangle, BO and CO will be the angle bisectors of B and C respectively.
Hence ∠OBC =
= 30°
and as given in the figure we can see that OB and OC are the radii of the given circle.
Hence they are of equal length.
The ΔOBC is an isosceles triangle with OB = OC
In ΔOBC,
∠OBC = ∠OCB as they are angles opposite to the two equal sides of an isosceles triangle.
Hence, ∠OBC = 30° and ∠OCB = 30°
Since the sum of all angles of a triangle is 180°
Hence in triangle OBC, ∠OCB + ∠OBC + ∠BOC + BOC = 180°
30° + 30° + ∠BOC= 180°
60° + BOC = 180°
∠BOC = 180° – 60°
∠BOC = 120°
Hence ∠BOC =120° and ∠OBC =30°
Question 2
In the given figure, a square is inscribed in a circle with centre O. Find:
(i) ∠BOC
(ii) ∠OCB
(iii) ∠COD
(iv) ∠BOD
Is BD a diameter of the circle?
……………….
Answer
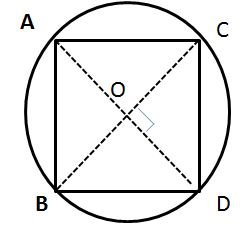
n the given figure we can extend the straight line OB to BD and CO to CA
Then we get the diagonals of the square which intersect each other at 90 by the property of Square.
From the above statement, we can see that
∠COD = 90°
The sum of the angle ∠BOC and ∠COD is 180° as BD is a straight line.
Hence ∠BOC + ∠OCD = ∠BOD = 180°
∠BOC + 90° = 180°
∠BOC + 180° – 90°
∠BOC = 90°
We can see that the OCB is an isosceles triangle with sides OB and OC of EQual length as they are the radii of the same are.
In ΔOCB,
∠OBC = ∠OCB as they are opposite angles to the two equal sides of an isosceles triangle.
Sum of all the angles of a triangle is 180°
so, ∠OBC + ∠OCB + ∠BOC =180°
∠OBC + ∠OBC + 90° = 180° as, ∠OBC = ∠OCB
2∠OBC = 180° – 90°
2∠OBC = 90°
2∠OBC = 45°
as ∠OBC = ∠OCB So,
∠OBC = OCB = 45°
Yes BD is the diameter of the order.
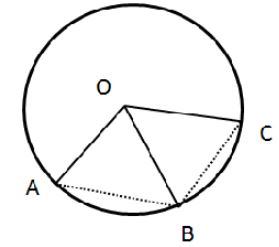
Question 3
In the given figure, AB is a side of regular pentagon and BC is a side of regular hexagon.
(i) ∠AOB
(ii) ∠BOC
(iii) ∠AOC
(iv) ∠OBA
(v) ∠OBC
(vi) ∠ABC
Answer
As given that AB is the side of a pentagon the angle subtended by each arm of the pentagon at the center of the circle is = = 72°
Thus angle ∠AOB = 72°
Similarly, as BC is the side of a hexagon hence the angle subtended by BC at the center is = i.e. 60°
∠BOC = 60°
Now ∠AOC = ∠AOB + ∠BOC =72° + 60° = 132°
The triangle thus formed, AOB is an isosceles triangle with OA = OB as they are radii of the same circle.
Thus ∠OBA = ∠BAO as they are opposite angles of equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°
so, ∠AOB + ∠OBA + ∠BAO = 180°
⇒ 2∠OBA + 72° = 180° as, ∠OBA = ∠BAO
⇒ 2∠OBA = 180° – 72°
⇒ 2∠OBA = 180°
⇒ 2∠OBA =54°
as, ∠OBA = ∠BAO So,
∠OBA = ∠BAO = 54°
The triangle thus formed, ΔBOC is an isosceles triangle
with OB = OC as they are radii of the same are.
Thus ∠OBC = ∠OCB as they are opposite angles of equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°
so, ∠BOC + ∠OBC + ∠OCB = 180°
2∠OBC + 60° = 180° as , ∠OBC = ∠OCB
2∠OBC = 180° – 60°
2∠OBC = 120°
∠OBC = 60°
as ∠OBC = ∠OCB
So, ∠OBC = ∠OCB
∠ABC = ∠OBA + ∠OBC = 54° + 60°= 144°
Question 4
In the given figure, arc AB and arc BC are equal in length. If ∠AOB = 48°, find:
(i) ∠BOC
(ii) ∠OBC
(iii) ∠AOC
(iv) ∠OAC
Answer
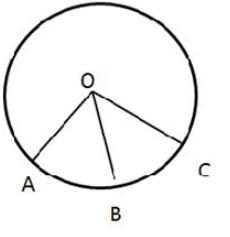
We know that the arc of equal lengths subtends equal angles at the center.
hence ∠AOB = ∠BOC = 48°
Then ∠AOC = ∠AOB + ∠BOC = 48° + 48° = 96°
The triangle thus formed, ΔBOC is an isosceles triangle with OB = OC as they are radii of the same circle.
Thus ∠OBC = ∠OCB as they are opposite angles of equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°.
So, ∠BOC + ∠OBC + ∠OCB = 180°
2∠OBC + 48° = 180° as ∠OBC = ∠OCB
2∠OBC = 180° – 48°
2∠OBC = 132°
∠OBC = 66°
as ∠OBC = ∠OCB
So, ∠OBC = ∠OCB = 66°
The triangle thus formed, ΔAOC is an isosceles triangle with OA = OC as they are radii of the same circle.
Thus ∠OAC = ∠OCA as they are opposite angles of equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°.
So, ∠COA + ∠OAC + ∠OCA = 180°
2∠OAC + 96° = 180° as, ∠OAC = ∠OCA
2∠OAC = 180° – 96°
2∠OAC = 84°
∠OAC = 42°
as ∠OCA = ∠OAC
So, ∠OCA = ∠OAC = 42°.
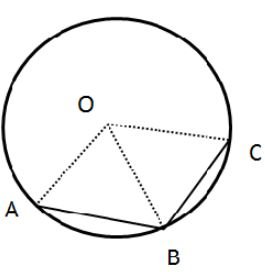
Question 5
In the given figure, the lengths of arcs AB and BC are in the ratio 3:2.
If ∠AOB = 96°, find:
(i) ∠BOC
(ii) ∠ABC
Answer
We know that for two arcs are in ratio 3: 2 then
∠AOB: ∠BOC = 3: 2
As give ∠AOC = 96°
So, 3x = 96
x = 32
There ∠BOC = 2 x 32 = 64°
The triangle thus formed, ΔAOB is an isosceles triangle with OA = OB as they are radii of the same circle.
Thus ∠OBA = ∠BAO as they are opposite angles of equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°
So, ∠AOB + ∠OBA + ∠BAO = 180°
2∠OBA + 96° = 180° as, ∠OBA = ∠BAO
2∠OBA = 180° – 96°
2∠OBA = 84°
∠OBA = 42°
as, ∠OBA = ∠BAO So,
∠OBA = ∠BAO = 42°
The triangle thus formed, ΔBOC is an isosceles triangle with OB = OC as they are radii of the same circle.
Thus ∠OBC = ∠OCB as they are opposite angles of equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°
So, ∠BOC + ∠OBC + ∠OCB = 180°
2∠OBC + 64° = 180° as, ∠OBC = ∠OCB
2∠OBC = 180° – 64°
2∠OBC = 116°
∠OBC = 58°
As ∠OBC = ∠OCB So,
∠OBC = ∠OCB = 58°
∠ABC = ∠BOA + ∠OBC = 42°+ 58° = 100°
Question 6
In the given figure, AB = BC = DC and ∠AOB = 50°.
(i) ∠AOC
(ii) ∠AOD
(iii) ∠BOD
(iv) ∠OAC
(v) ∠ODA
Answer
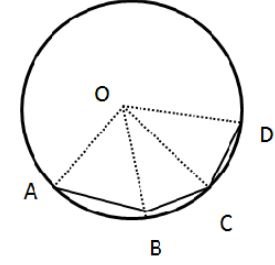
Since arc AB and BC are equal.
So, ∠AOB = ∠BOC = 50°
Now,
∠AOC = ∠AOB + ∠BOC = 50° + 50° = 100°
As arc AB, arc BC and arc CD so,
∠AOB = ∠BOC = ∠COD = 50°
∠AOD = ∠AOB + ∠BOC + ∠COD = 50° + 50° + 50° = 150°
Now, ∠BOD = ∠BOC + ∠COD
∠BOD = 50° + 50°
∠BOD = 100°
The triangle thus formed, ΔAOC is an isosceles triangle with OA = OC as they are radii of the same circle.
Thus ∠OAC = ∠OCA as they are opposite angles of equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°
So, ∠AOC + ∠OAC + ∠OCA = 180°
2∠OAC + 100° = 180° as, ∠OAC = ∠OCA
2∠OAC = 180° – 100°
2∠OAC = 80°
∠OAC = 40°
as ∠OCA = ∠OAC So,
∠OCA = ∠OAC = 40°
The triangle thus formed, ΔAOD is an isosceles triangle with OA = OD as they are radii of the same circle.
Thus, ∠OAD = ∠ODA as they are opposite angles of equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°
So, ∠AOD + ∠OAD + ∠ODA = 180°
2∠OAD + 150° = 180° as, ∠OAD = ∠ODA
2∠OAD = 180° – 150°
∠OAD = 30°
as ∠OAD = ∠ODA So,
∠OAD = ∠ODA = 15°.
Question 7
In the given figure, AB is a side of a regular hexagon and AC is a side of a regular eight sided polygon. Find:
(i) ∠AOB
(ii) ∠AOC
(iii) ∠BOC
(iv) ∠OBC
Answer
Question 8
In the given figure, O is the center of the circle and the length of arc AB is twice the length of arc BC. If ∠AOB = 100°,
find: (i) ∠BOC (ii) ∠OAC
Answer

We know that when two arcs are in ratio 2: 1 then the subtended by them is also in ratio 2: 1
As given arc AB is twice the length of arc BC.
Therefore, arc AB: arc BC = 2: 1
Hence, ∠AOB: ∠BOC = 2: 1
Now given that ∠AOB = 100°.
So, ∠BOC =
Now, ∠AOC = ∠AOB + ∠BOC = 100° + 50° = 150°.
The triangle thus formed, ∠AOC is an isosceles triangle with OA = OC as they are radii of the same circle.
Thus,
∠OAC = ∠OCA as they are opposite angles of equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°.
So, ∠COA + ∠OAC + ∠OCA = 180°
2∠OAC + 150° = 180° as, ∠OAC = ∠OCA
2∠OAC = 180° – 150°
2∠OAC = 30°
∠OAC = 15°
as ∠OCA = ∠OAC So,
∠OCA = ∠OAC = 15°.
Exercise-17 D Circle Theorem Class-9th Concise Selina ICSE Mathematics Solutions
Question 1
The radius of a circle is 13 cm and the length of one of its chords is 24 cm. Find the distance of the chord from the centre.
Answer
Question 2
Prove that equal chords of congruent circles subtend equal angles at their centre.
Answer
Question 3
Draw two circles of different radii. How many points these circles can have in common? What is the maximum number of common points?
Answer
So, the circle can have 0, 1 or 2 points in common.
The maximum number of common points is 2.
Question 4
Suppose you are given a circle. Describe a method by which you can find the centre of this circle.
Answer
Question 5
Given two equal chords AB and CD of a circle with centre O, intersecting each other at point P. Prove that:
(i) AP = CP
(ii) BP = DP
Answer
Question 6
In a circle of radius 10 cm, AB and CD are two parallel chords of lengths 16 cm and 12 cm respectively. Calculate the distance between the chords, if they are on:
(i) the same side of the centre.
(ii) the opposite sides of the centre.
Answer
Question 7
In the given figure, O is the centre of the circle with radius 20 cm and OD is perpendicular to AB.
If AB = 32 cm, find the length of CD
Answer
Question 8
In the given figure, AB and CD are two equal chords of a circle, with centre O.
If P is the mid-point of chord AB, Q is the mid-point of chord CD and ∠POQ = 150°, find ∠APQ.
Answer
It is given in the question that point.
P is the mid-point of the chord AB and Point Q is the mid-point of the CD.
⇒ ∠APO = 90° …( as the straight line drawn from the center of a circle to bisect a chord, which is not a diameter, is at the right angle to the chord. )
As chords, AB and CD are equal therefore they are equidistant from the center i.e; PO = OQ …( ∵ Equal chords of a circle are equidistant from the center)
Now, the ΔPOQ is an isosceles triangle with OP = OQ as its two equal sides of an isosceles triangle.
The sum of all the angles of a triangle is 180°.
⇒ ∠POQ + ∠OPQ + ∠PQO = 180°
⇒ ∠OPQ + ∠POQ + 150° = 180° …( Given: ∠POQ = 150° )
⇒ 2∠OPQ = 180° – 150° …( As, ∠OPQ = ∠PQO )
⇒ 2∠OPQ = 30°
⇒ ∠OPQ = 15°
As ∠APO = 90°
⇒ ∠APQ + ∠OPQ = 90°
⇒ ∠APQ = 90° – 15° ….( As, ∠OPQ = 15° )
⇒ ∠APQ = 75°.
Question 9
In the given figure, AOC is the diameter of the circle, with centre O.
If arc AXB is half of arc BYC, find ∠BOC.
Answer
Given :
1. AOC is the diameter.
2. Arc AXB = Arc BYC
From Arc AXB = Arc BYC We can see that
Arc AXB : Arc BYC = 1 : 2
⇒ ∠BOA : ∠BOC = 1 : 2
Since AOC is the diameter of the circle hence,
∠AOC = 180°
Now,
Assume that ∠BOA = x° and ∠BOC = 2x°
∠AOC = ∠BOA + ∠BOC = 180°
⇒ x + 2x = 180°
⇒ 3x = 180°
⇒ x = 60°
Hence, ∠BOA = 60° and ∠BOC = 120°.
Question 10
The circumference of a circle, with center O, is divided into three arcs APB, BQC, and CRA such that:
……………………..
Find ∠BOC.
Answer
then
Arc APB = 2k, Arc BQC = 3k, Arc CRA = 4k
or
Arc APB : Arc BQC : Arc CRA = 2 : 3 : 4
⇒ ∠AOB : ∠BOC : ∠AOC = 2 : 3 : 4
and therefore,
and ∠AOB = 2k°, ∠BOC = 3k°, and ∠AOC = 4k°
Now,
Angle in a circle is 360°
So, 2k + 3k + 4k = 360°
⇒ 9k = 360°
⇒ k = 40°
Hence,
∠BOC = 3 x 40° = 120°.
— End of Circle Theorem Class-9th Concise Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -9