Circles Class 10 OP Malhotra Exe-14B ICSE Maths Solutions Ch-14 questions as latest prescribe guideline for upcoming exam. In this article you would learn Cyclic Properties of a Circle. Visit official Website CISCE for detail information about ICSE Board Class-10 Mathematics.

Circles Class 10 OP Malhotra Exe-14B ICSE Maths Solutions Ch-14
| Board | ICSE |
| Publications | S Chand |
| Subject | Maths |
| Class | 10th |
| Chapter-14 | Circles |
| Writer | OP Malhotra |
| Exe-14B | Cyclic Properties of a Circle |
| Edition | 2024-2025 |
Cyclic Properties of a Circle
- Inscribed angles subtended by the same arc are equal.
- Central angles subtended by arcs of the same length are equal.
- The central angle of a circle is twice any inscribed angle subtended by the same arc.
- Angle inscribed in semicircle is 90°.
- An angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment.
- The opposite angles of a cyclic quadrilateral are supplementary
- The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.
- A radius or diameter that is perpendicular to a chord divides the chord into two equal parts and vice versa.
- A tangent to a circle is perpendicular to the radius drawn to the point of tangency.
- When two segments are drawn tangent to a circle from the same point outside the circle, the segments are equal in length.
Exercise- 14B Cyclic Properties of a Circle
(Circles Class 10 OP Malhotra Exe-14B ICSE Maths Solutions Ch-14)
Que-1: In the fig., in △ABC, AB = AC, and XY || BC. Prove that BCYX is a cyclic quadrilateral.
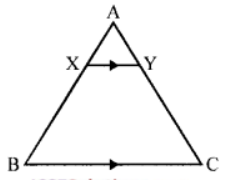
Sol: Given : In the figure, in △ABC, AB = AC. XY || BC
In △ABC,
XY || BC
∴∠AXY = ∠ABC (Corresponding angles)
But △ABC = ∠ACB (∵AB = AC)
∴∠AXY = ∠ACB
But Ext. ∠AXY is equal to its interior opp. ∠ACB
∴ BCYX is a cyclic quadrilateral Hence proved.
Que-2: In the figure, In a quad. ABCD, ext. ∠XCD = int. opp ∠A. Prove that the quad. ABCD is a cyclic quad.
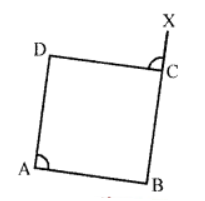
Sol:Given : In the figure, in quad. ABCD
BC is produced to X
Ext. ∠XCD = Int. opp. ∠A
∠XCD + ∠DCB = 180° (Linear pair)
∠A = ∠DCB = 180° (∵ ∠A = ∠XCD)
But these are opposite angles of a quad.
∴ Quad ABCD is a cyclic Hence proved.
Que-3: In the figure, PQR is an isosceles triangle with PQ equal to PR. A circle passes through Q and R and intersects the sides PQ and PR at points S and T respectively. Prove that QR || ST.
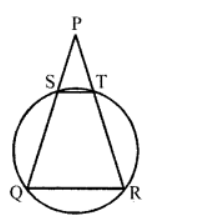
Sol: Given : In △PQR, PQ = PR
A circle passing through Q and R, intersects PQ and PR at S and T respectively. ST is joined
In △PQR
PQ = PR (given)
∴ ∠Q = ∠R ….(i) (Angles opposite to equal sides)
∵ SQRT is a cyclic quadrilateral
∴ Ext. ∠S = Int. opp. ∠R …(ii)
From (i) and (ii)
∠Q = ∠S
But these are corresponding angles
∴ QR || ST Hence proved.
Que-4: In the figure, AB is the common chord of two circles. If AC and AD are diameters, prove that D, B and C are in a straight line. O1 and O2 are the centres of the circles.
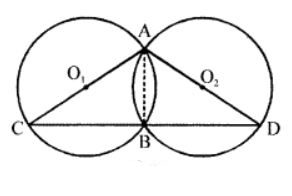
Sol: Given : Two circles with centres O1 and O2
intersect each other at A and B
AO1C and AO2D are diameters
∵ AC is the diameter of circle of centre O1
∴ ∠ABC = 90° (Angle in a semicircle)
Similarly
∠ABD = 90° (Angle in a semicircle)
Adding we get,
∠ABC + ∠ABD = 90° + 90° = 180°
∴ CBD is a straight line
Hence D, B and C are in the same straight line Hence proved.
Que-5: In figure, AB is the diameter of the circle whose centre is O. AD and BC are perpendiculars to the line XY. CB meets the circle at E. Prove that CE = AD.
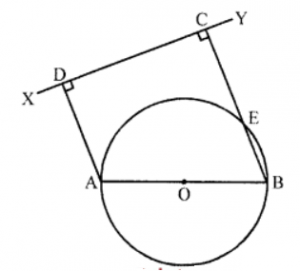
Sol: Given : In a circle with centre O, AB is its diameter AD ⊥ XY and BC ⊥ XY which intersects the circle at E
Join A, E.
∠AEB = 90° (Angle in a semicircle)
∴ ∠AEC = 90°
(∵ ∠AEB + ∠AEC = 180° linear pair)
But ∠C = ∠D = 90°
(∵ AD and EC are perpendicular to XY)
∴ AECD is a rectangle
∵ Opposite sides of a rectangle are equal
∴ CE =AD Hence proved.
Que-6: In fig., AB and CD are parallel chords of a circle whose diameter is AC. Prove that AB = CD.
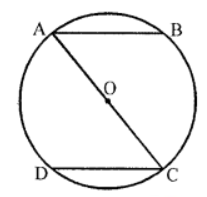
Sol: Given : In a circle with centre O, AC is its diameter and chord AB || CD
Join OB and OD
In AAOB and ACOD,
OA = OC
OB = OD (radii of the same circle)
∠BAO = ∠OCD (Alternate angles)
∴ △AOB ≅ △COD (SSA axiom)
∴ AB = CD Hence proved.
Que-7: In figure, APB and CQD are straight lines through the points of intersection of two circles. Prove
(i) AC || BD,
(ii) ∠CPD = ∠AQB (SC)
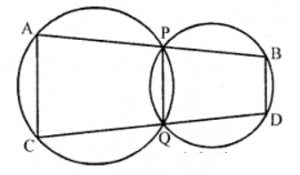
Sol: Given : Two circles intersect each other at P and Q
Lines APB and CQD are drawn from the point of intersection respectively PQ, AC, BD and AQ, QB, CP and PD are joined
(i) ∵ APQC is a cyclic quad.
∴ Ext. ∠BPQ = Int. opp. ∠C ….(i)
∵ PBDQ is a cyclic quad.
∴ ∠BPQ + ∠D = 180° (sum of opp. angles)
⇒ ∠C + ∠D = 180° {from (∠)}
But these are co-interior angles
∴ AC || BQ
(ii) In △AQB and △CPD,
∠PAQ = PCQ (Angles in the same segment)
∠PBQ = ∠PDQ (Angles in the same segment)
or ∠BAQ = ∠ABQ
∠ABQ = ∠PDC
∴ △AQB ~ △APD (AA axiom)
∴ Third angle = Third angle
⇒ ∠AQB = ∠CPD Hence proved.
Que-8: Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
Sol: Given: ABCD is a rhombus whose diagonals AC and BD intersect each other at O. A circle with AB as diameter is drawn.
Let the circle drawn on AB as diameter does not passes through O, let it intersect AC at P
Join PB
The ∠APB = 90° (Angle in a semicircle)
But ∠AOB = 90°
(∵ The diagonals bisect each other at right angles)
∴ ∠APB = ∠AOB
But it is not possible because ∠APB is the exterior angle of AOPB and an exterior angle of a triangle is always greater than its interior opposite angle
∴ Our supposition is wrong
Hence the circle will pass through O Hence proved.
Que-9: If two non-parallel sides of a trapezium are equal, it is cyclic. OR An isosceles trapezium is always cyclic.
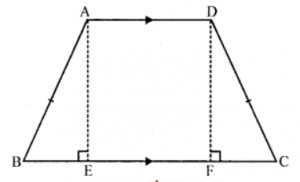
Sol: Given : An isosceles trapezium ABCD in
which AD || BC and AB = DC
In right △ABE and △DCF
Hyp. AB = DC (given)
Side AE = DF (Distance between two parallel lines)
∴ △ABE ≅ △DCF (RHS axiom)
∴ ∠B = ∠C (c.p.c.t.)
Now AD || BC
∴ ∠DAB + ∠B = 180° (Co-interior angles)
⇒ ∠DAB + ∠C = 180° (∵ ∠B = ∠C proved)
But these are sum of opposite angles of a quad.
∴ ABCD is a cyclic. Hence proved.
Que-10: Prove that the sum of the angles in the four segments exterior to a cyclic quadrilateral is equal to 6 right angles.
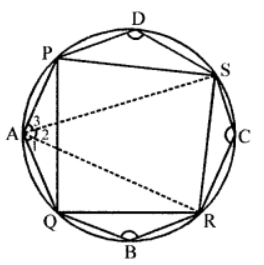
Sol: Given : PQRS is a cyclic quadrilateral
∠A, ∠B, ∠C and ∠D are angles in the four segment so formed exterior to the cyclic quadrilateral
Join AS and AR
In cyclic quad. ASDP,
∠PAS + ∠D = 2 rt. angles ….(i) (Sum of opposite angles)
Similarly in cyclic quad. ARBQ,
∠RAQ + ∠B = 2 rt. angles ….(ii)
and in cyclic quad. ARCS,
∠SAR + ∠C = 2rt. angles ….(iii)
Adding (i), (ii) and (iii)
∠PAS + ∠D + ∠RAQ + ∠B + ∠SAR + ∠C = 2 + 2 + 2 = 6rt. angles
⇒ PAS + ∠SAR + ∠RAQ + ∠B + ∠C + ∠D = 6 rt. angles
⇒ ∠A + ∠B + ∠C + ∠D = 6 rt. angles Hence proved.
Que-11: (i) In figure, O is the circumcenter of △ABC and OD ⊥ BC. Prove that ∠BOD = ∠A.
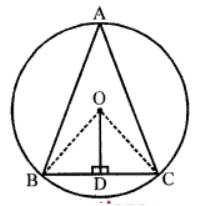
Sol: Given : O is the circumcentre of △ABC
OD ⊥ BC. OB and OC are joined
Arc BC subtends ∠BOC at the centre and ∠BAC at the remaining part of the circle
∴ ∠BOC = 2 ∠BAC ….(i)
In △OBC, OD ⊥ BC
OB = OC (radii of the same circle)
∴ OD bisects ∠BOC
⇒ ∠BOD = (1/2) ∠BOC ….(ii)
From (i) and (ii)
∠BOD = (1/2) ∠BAC = ∠BAC
Hence ∠BOD = ∠A
Hence proved.
Que-12: ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EF || DC.
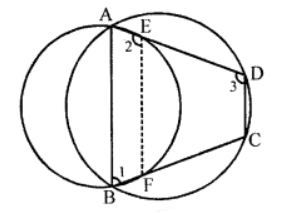
Sol: Given : ABCD is a cyclic quadrilateral
A circle passing through A and B meet AD
and BC at E and F respectively
EF is joined
ABCD is a cyclic quad.
∴ ∠1 + ∠3 = 180° ….(i) (Sum of opposite angles)
Similarly ABFE is a cyclic quadrilateral
∴ ∠1 + ∠2 = 180° ….(ii)
From (i) and (ii)
∠1 + ∠3 = ∠1 + ∠2 ⇒ ∠3 = ∠2
But these are corresponding angles
∴ EF || DC Hence proved.
–: End of Circles Class 10 OP Malhotra Exe-14B ICSE Maths Solutions Ch-14 :–
Return to :- OP Malhotra S Chand Solutions for ICSE Class-10 Maths
Thanks
Please Share with Your Friends


